Inhoud
Al lezend in het boek MindF*ck van Victor Mids en Oscar Verpoort werd ik geïnspireerd tot het schrijven van dit stukje. In het boek komt (in mijn eigen bewoordingen) de volgende truc voor: “Vraag iemand twee willekeurige getallen onder elkaar te schrijven (niet al te groot, want de persoon moet ermee gaan rekenen). Laat de persoon nu deze twee getallen optellen en de som onder het tweede getal zetten. Vraag nu aan deze persoon om het tweede en derde getal bij elkaar op te tellen en deze som daar weer onder te zetten. Laat hem/haar dit herhalen totdat er 10 getallen onder elkaar staan. Nu zeg je dat je in een oogwenk deze 10 getallen bij elkaar zult optellen. De persoon laat het blaadje met de 10 getallen aan je zien en je zet er een streep onder met daaronder de som van de getallen. Laat de persoon deze getallen ook bij elkaar optellen (rekenmachine toegestaan) en hij/zij zal verbaasd zijn over de uitkomst. Jij had het namelijk goed! De truc is als volgt: Kijk naar het zevende getal en vermenigvuldig dit met 11 (x10 + 1) en zet dit getal onder de streep. Onafhankelijk van de gekozen getallen werkt dit altijd.” Tot zover het boek. Maar hoe zit dit nu? Daar geeft het boek geen antwoord op. Dus gaan we zelf maar aan de slag. De meeste mensen hebben wel gehoord over de rij van Fibonacci. Deze rij bestaat uit de volgende getallen: 1, 1, 2, 3, 5, 8, 13, 21, 34, … en is opgebouwd volgens een vast patroon: De eerste twee termen zijn 1 en de daarop volgende termen zijn de som van de voorgaande twee termen. In formulevorm: We definiëren nu de Fibonacci-som als volgt: Sn is dus de cumulatieve som van alle Fibonacci-getallen t/m de ne. Kijk even naar de volgende tabel: In bovenstaande tabel zijn S6 en S10 rood en F5 en F7 groen gemarkeerd. Ik kan namelijk S6 uitdrukken in F5 en evenzo S10 in S7 en wel als volgt: S6 = 4 x F5 en S10 = 11 x F7. Nu kan ik natuurlijk iedere Sn in een Fm uitdrukken (bijvoorbeeld S5 = 6 x F3), maar met deze twee is toch iets bijzonders aan de hand. We maken even een nieuwe tabel: En nog steeds geldt: S6 = 4 x F5 en S10 = 11 x F7 (merk op dat S5 = 6 3/11 x F3). Dit verdient nader onderzoek. In Excel even een grotere tabel gemaakt: Wanneer je in deze tabel verschillende waarden voor F1 en F2 invult dan blijkt dat de gele cellen onveranderlijk blijven Uit de tabel haal ik de volgende onveranderlijke Sn’s: S6 = 4 x F5 De volgende vragen dringen zich nu op: Uit de voorbeelden en uit de grote tabel blijkt dat: S4n+2 = Vn x F2n+3. Dit is dus het antwoord op vraag 1. We weten uit de voorbeelden dat: V1 = 4, Deze rij getallen biedt niet meteen houvast om een gemakkelijke regel voor V5, V6…Vn te bepalen. Hiervoor moeten we wat verder onderzoek doen. Laten we eens kijken naar S10 met als startgetallen F1=A=4 en F2=B=7: S10 = 836 = 55A + 88B = 11(5A+8B). Maar nu is 5A+8B gelijk aan F7 (kijk maar in de tabel hierboven). Dus is S10 = 11 x F7. A en B zijn hier willekeurig en zowel S10 als F7 zijn in dezelfde A en B uitgedrukt (nl. 5A+8B) waarmee de vermenigvuldiger (11) dus invariant is. Hiermee is dus (min of meer) vraag 3 beantwoord. Kijk nog eens goed naar de factoren van A en B in de bovenstaande tabel. De factoren bij A en bij B volgen weer keurig de (standaard) rij van Fibonacci! En dit geeft ons houvast voor een formule voor de vermenigvuldigers Vn. V2=11=(F10-F11-1)/(F5-F6), En hiermee is ook vraag 2 opgelost. We hebben dus voor de mooie Sn’s de volgende formule: Tot slot zou het mooi zijn als we in de formule voor Sn alleen maar afhankelijk zouden zijn van gewone getallen al dan niet in combinatie met n, ofwel dat we Sn kunnen uitdrukken in termen van n. Dit betekent dat we dus een formule voor Fn uitgedrukt in n moeten hebben. Welnu, deze is er: Deze formule is (vrij eenvoudig) te bewijzen door middel van volledige inductie, maar dat laat ik graag aan de lezer over. De getallen (1+√5)/2 en (1-√5)/2 komen niet zo maar uit de lucht vallen. Wanneer je kijkt naar het quotiënt van twee opeenvolgende Fibonacci getallen, dus Fm/Fm-1, en je gaat steeds verder in de rij dat blijkt dat het quotiënt naar een bepaalde limiet-waarde toegaat. Deze limiet-waarde blijkt (1+√5)/2 te zijn. Kijk maar eens: Stel : De tweede = heeft te maken met de eigenschappen van limieten (n gaat toch naar oneindig). Denk nog even aan de recurente betrekking van Fn: dan krijgen we nu: Bedenkt bij de laatste limiet dat Fn-1/Fn = 1 / (Fn/Fn-1). We hebben dus L = 1 + 1/L. Dat kunnen we herschrijven als L2 = L + 1 ofwel L2 – L – 1 = 0. En met behulp van de abc-formule vinden we voor L de waardes (1+√5)/2 en (1-√5)/2. Tussen haakjes (het getal (1+√5)/2 staat ook wel bekend als de waarde van de gulden-snede en wordt ook wel φ (phi) genoemd). Met al deze kennis kunnen we nu een formule voor mooie Sn’s uitgedrukt in n geven: Wat kan wiskunde toch mooi zijn!Inleiding
Fibonacci
n
1
2
3
4
5
6
7
8
9
10
Fibn
1
1
2
3
5
8
13
21
34
55
Sn
1
2
4
7
12
20
33
54
88
143
n
1
2
3
4
5
6
7
8
9
10
Fibn
4
7
11
18
29
47
76
123
199
322
Sn
4
11
22
40
69
116
192
315
514
836
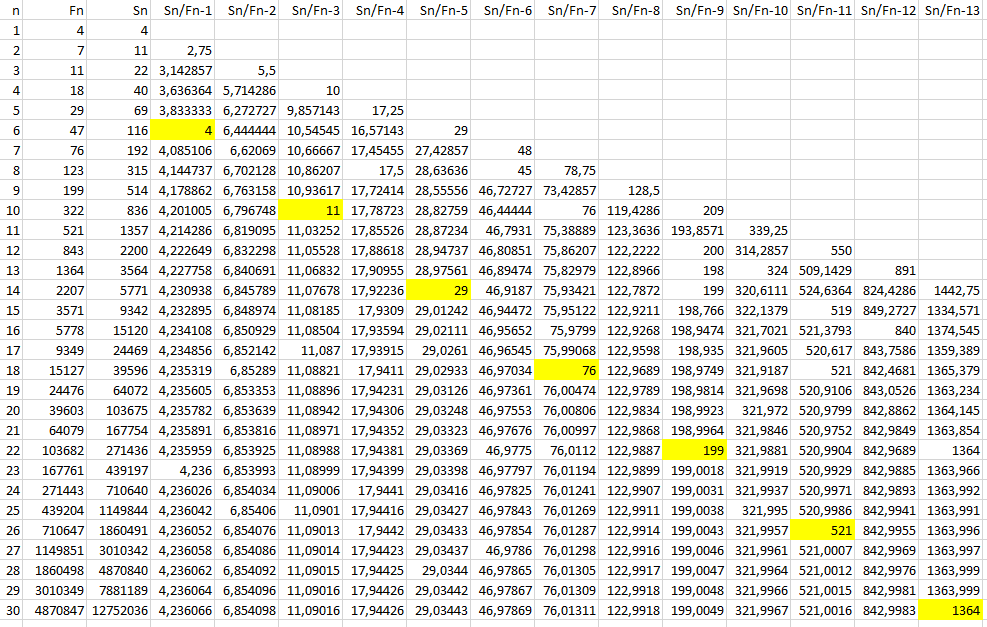
S10 = 11 x F7
S14 = 29 x F9
S18 = 76 x F11
…Vragen
V2 = 11,
V3 = 29,
V4 = 76…
n
Fn
A
B
1
4
1A
2
7
1B
3
11
1A
+
1B
4
18
1A
+
2B
5
29
2A
+
3B
6
47
3A
+
5B
7
76
5A
+
8B
8
123
8A
+
13B
9
199
13A
+
21B
10
322
21A
+
34B
—+
—+
—+
836
55A
88B
Vn=(F4n+2+F4n+3)/(F2n+1+F2n+2).Gulden-snede
Fibonacci sommen
\left\{\begin{matrix}F_{1}=F_{2}=1\\F_{n}=F_{n-1}+F_{n-2},\forall n>2\end{matrix}\right.
s_{n}=\sum_{i=1}^{n}F_{i}
S_{4n+2}=\frac{F_{4n+2}+F_{4n+3}\text{ - }1}{F_{2n+1}+F_{2n+2}}\cdot F_{2n+3}
F_{n}=\frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{n}\text{ - }\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{n}}{\sqrt{5}}
L=\lim_{n \to \infty }\frac{F_{n}}{F_{n\text{ - }1}}=\lim_{n \to \infty }\frac{F_{n+1}}{F_{n}}
F_{n+1}=F_{n}+F_{n\text{ - }1}
L=\lim_{n \to \infty}\frac{F_{n+1}}{F_n}=\lim_{n \to \infty}\frac{F_{n}+F_{n\text{ - }1}}{F_n}=\lim_{n \to \infty}\frac{F_{n}}{F_n}+\lim_{n \to \infty}\frac{F_{n\text{ - }1}}{F_n}=1+\frac{1}{L}
S_{4n+2}=\frac{\frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{4n+2}\text{ - }\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{4n+2}}{\sqrt{5}}+\frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{4n+3}\text{ - }\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{4n+3}}{\sqrt{5}}\text{ - }1}{\frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{2n+1}\text{ - }\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{2n+1}}{\sqrt{5}}+\frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{2n+2}\text{ - }\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{2n+2}}{\sqrt{5}}}\cdot \frac{\left ( \frac{1+\sqrt{5}}{2} \right )^{2n+3}\text{ - }\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{2n+3}}{\sqrt{5}}