Inhoud
Deze pagina gaat over onopgeloste problemen in de wiskunde die eenvoudig zijn te formuleren zodat een kind, bij wijze van spreken, begrijpt waarover het gaat maar waar de wiskunde tot op heden geen oplossing voor heeft kunnen geven. We gaan dus niet in op problemen zoals de Riemann hypothese. Is het belangrijk dat deze, of soortgelijke, problemen worden opgelost? Wanneer u beroemd wil worden, los dan één van deze problemen op! Er zijn oneindig veel priemgetallen. Dat is al eeuwen geleden bewezen (zie Bewijzen) en er zijn meer bewijzen voor deze stelling. Laten we eens kijken naar het begin van de rij priemgetallen: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199 Als we kijken naar de onderlinge verschillen tussen twee opeenvolgende priemgetallen dan valt op dat er veel paren zijn met een onderling verschil van 2: 3 en 5, 5 en 7, 11 en 13, 17 en 19, 29 en 31, 41 en 43, 59 en 61, 71 en 73, 101 en 103, 107 en 109, 137 en 139, 149 en 151, 179 en 181, 191 en 193, 197 en 199, … Deze paren heten priemtweelingen, ofwel een priemtweeling is een tweetal opeenvolgende priemgetallen met onderling verschil van 2. Hoe ver men ook in de rij (opeenvolgende) priemgetallen heeft gekeken, overal komen ze voor. [Excuses! Dit is een aangepaste tekst omdat er in de vorige editie (ernstige) fouten waren geslopen.] Een volmaakt getal, ook wel perfect getal genoemd, is een getal dat je kunt schrijven als de som van de “echte” delers van dat getal. Onder de echte delers van een getal wordt verstaan: Alle delers behalve het getal zelf (zie ook Getal-eigenschappen). Dit verhaal gaat over even volmaakte getallen! Zo is 6 bijvoorbeeld een volmaakt getal, want de echte delers van 6 zijn 1, 2 en 3 en 1 + 2 + 3 = 6. Dit is ook het kleinste volmaakte getal. Het volgende getal is 28 = 1 + 2 + 4 + 7 + 14 en 1, 2, 4, 7 en 14 zijn de echte delers van 28. De volgende is 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248. Daarna komt 8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064. Volmaakte getallen worden dus, kennelijk, snel groter en dat is ook zo. Het 5e volmaakte getal is namelijk 33.550.336. Er is echter een mooie formule om volmaakte getallen te genereren: Als een priemgetal geschreven kan worden als 2n – 1 dan heet zo’n priemgetal een Mersenne-priemgetal, vernoemd naar de Franse priester en wiskundige Marin Mersenne (16e / 17e eeuw). Als 2n – 1 een Mersenne-priemgetal is, dan is n (de exponent) ook een priemgetal. Mersenne-priemgetallen worden aangegeven als Mp, waarbij p de exponent is (en p is dus priem). Laten we eens kijken naar de ontbindingen van de, tot nog toe in dit artikel, gevonden volmaakte getallen: 6 = 21 × (22 – 1) = 21 × M2, De factoren tussen haakjes zijn allemaal Mersenne-priemgetallen. Merk op dat M11 = 2047 geen priemgetal is (2047 = 23 × 89). De formule voor een volmaakt getal is: Als (2p – 1) priem is dan is 2p-1 × (2p – 1) een volmaakt getal. Het volgende priemgetal is 17 en 217-1 is priem dus 216 × (217 – 1) = 8.589.869.056 is het volgende (6e) volmaakte getal. Het is wiskundig bewezen dat ieder even volmaakt getal volgens bovenstaande formule te maken is (en vice versa, dus ieder even volmaakt getal is van de vorm 2n-1 × (2n – 1) waarbij 2n – 1 een priemgetal is). Bewijs Alvorens we naar het generieke bewijs gaan kijken gaan we eerst 496 (3e perfecte getal) “ontleden”, want dit geeft een concreet beeld van hoe het bewijs eruit gaat zien. 496 = 1 + 2 +4 + 8 + 16 + 31 + 62 + 124 + 248 (dit zijn de “echte” delers van 496). Omdat we zo meteen 31 buiten haakjes gaan halen voeg ik eerst 496 zelf toe aan de som. We krijgen dan dus 2 maal het perfecte getal 496: 2 × 496 = 1 + 2 +4 + 8 + 16 + 31 + 62 + 124 + 248 + 496 = Bedenk wel dat dit laatste resultaat dus 2 keer 496 is, dus 2 × 496 = 25 × (25 – 1). Maar dat betekent dus dat 496 = 24 × (25 – 1), precies volgens de formule! We gaan nu kijken naar de som der delers van 2n-1 × (2n – 1) waarbij 2n-1 een priemgetal is. De delers van een 2e macht zijn niets anders dan de getallen 2n, waarbij n loopt van 0 naar de exponent. We krijgen dus: (1 + 21 + 22 + 23 + … + 2n-2 + 2n-1)(2n – 1) = Merk op dat het laatste getal [2n-1(2n – 1)] het getal zelf is; dit is dus de dubbele som! We gaan verder: = (1 + 21 + 22 + 23 + … + 2n-2 + 2n-1) + (2n-1)(1 + 21 + 22 + 23 + … + 2n-2 + 2n-1) = Stel nu T = 1 + 21 + 22 + 23 + … + 2n-2 + 2n-1, dan is En als we deze twee netjes onder elkaar zetten dan kunnen we ze van elkaar aftrekken: 2T = 0 + 21 + 22 + 23 + … + 2n-2 + 2n-1 + 2n We hebben dus 2T – T = T = 2n – 1. Dus 2n(1 + 21 + 22 + 23 + … + 2n-2 + 2n-1) = En tot slot moeten we ons bedenken dat we met een dubbele som te maken hebben waardoor we het laatste getal [2n(2n-1)] door 2 moeten delen en er 2n-1(2n-1) over blijft! Alle, tot nog toe gevonden volmaakte getallen zijn even. En dat leidt tot de vraag: Dit probleem kwam ik tegen op Numberphile in een artikel van Matt Parker. Omdat het niet echt een naam had heb ik dit zelf “Parker Product Chains” genoemd. Het gaat als volgt: Je krijgt zo een ketting van getallen. Alle getallen van 0 t/m 9 hebben een kettinglengte van 0 (triviaal). Het getal 10 (t/m 24) heeft een kettinglengte van 1. Het getal 10 is ook het eerste (kleinste) getal met een kettinglengte van 1: 10 → 0 (=1 × 0). Voor de rest van dit verhaal zoeken we steeds het kleinste getal met een bepaalde kettinglengte. Het getal 25 is het kleinste getal met een kettinglengte van 2 (10 → 0). Het getal 39 is het kleinste getal met een kettinglengte van 3 (27 → 14 → 4). Zie verder onderstaande tabel: En hier stopt de tabel… Tot op heden is er geen getal gevonden dat een kettinglengte groter dan 11 oplevert. Overigens heb ik de resultaten uit bovenstaande tabel met een Python-programmaatje verkregen. Met een wat uitgebreidere versie van dat Python-programma ben ik verder gaan zoeken. Hoe doet ie dat? Het is uiteraard onmogelijk om alle getallen tot tien octiljoen te testen. En daarom is de wiskunde zo handig. Lang niet alle getallen komen in aanmerking voor dit probleem. Als eerste moet je je realiseren dat bijvoorbeeld 123, 321, 132 etc. allemaal hetzelfde product opleveren, daarom hoef je alleen maar 123 te testen. Verder zal een 0 in een getal een product van 0 opleveren wat de ketting dus meteen stopt. Ook een 1 legt geen enkel gewicht in de schaal. En de combinatie van een even getal met 5 levert in de volgende stap ook een 0 op, waarmee de ketting dus weer tot een eind komt. En Python heeft de prettige eigenschap van zogenaamde “comprehensions”, dit is een manier om op een handige manier lijsten te vullen waar ik dankbaar gebruik van maak: En in de functie test kijk ik dan of er een even getal en een 5 in voorkomt. Het programma dat de informatie van bovenstaande tabel oplevert test daarvoor maar 173.603 getallen en dat is vele malen minder dan 277.777.788.888.899. Op mijn simpele laptopje heeft Python daar dan ook maar 1,8 seconden voor nodig. Het lijkt erop dat er geen getallen zijn met een langere ketting dan 11, maar dat moet dan wel bewezen worden. Nog zo’n mooi onopgelost probleem. Het vermoeden is vernoemd naar Lothar Collatz (1910 – 1990), een Duits wiskundige, die het vermoeden in 1937 opperde. Neem een willekeurig natuurlijk getal (dus positief geheel). Herhaal met dit nieuwe getal bovenstaande procedure. Het vermoeden is nu dat je altijd op 1 zult eindigen (of anders gezegd: Je komt in de loop 4 → 2 → 1 terecht). In wiskundige termen ziet het er als volgt uit: ∀ n ∈ℕ > 0 geldt: Voorbeelden: n = 5, dan 5 → 16 → 8 → 4 → 2 → 1, Inmiddels zijn alle getallen tot zo’n 300 triljoen getest en alle voldoen aan het vermoeden. Het kan dus zijn dat er getallen bestaan die ofwel nooit eindigen ofwel in een ander getal (of lus) eindigen. Voor meer informatie zie ook wikipedia. Een vreemd woord. Het de samentrekking van detwee Latijnse woorden “ALIus” (=anders) en “QUOT” (=hoeveel). In dit artikel, dat per slot over wiskunde gaat, is een aliquot niets anders dan de som van de echte delers van een getal. Voorbeelden: De echte delers van 12 zijn: 1, 2, 3, 4 en 6. De som van deze delers is 16. Dus de aliquot van 12 is 16. De echte delers van 8 zijn: 1, 2 en 4. De som van deze delers is 7. Dus de aliquot van 8 is 7. De aliquot van 12 wordt ook wel overvloedig, rijk of uitbundig (Engels=”abundant”) genoemd omdat de aliquot van 12 groter is dan 12 zelf. De aliquot van 8 wordt ook wel ontoerijkend of gebrekkig (Engels=”deficient”) genoemd omdat de aliquot van 8 kleiner is dan 8 zelf. De aliquot van een priemgetal is altijd 1. Dat is logisch want de delers van een priemgetal zijn altijd 1 en het priemgetal zelf. De aliquot van een volmaakt of perfect getal is het getal zelf. Ook dat is logisch want de definitie van een perfect getal is dat de som van de echte delers gelijk zijn aan het getal zelf. Tot zover de definities en voorbeelden. Een aliquot-rij is een rij van aliquots waarbij de vorige aliquot dient als input van de volgende aliquot. Voorbeelden: De aliquot-rij beginnend met 12 luidt: (12,) 16, 15, 9, 4, 3, 1. Deze aliquot-rij heeft een lengte van 6 (we rekenen het startgetal niet mee). De aliquot-rij beginnend met 8 luidt: (8,) 7, 1 en heeft een lengte van 2. De aliquot-rijen van priemgetallen zijn 1 en hebben een lengte van 1. Kijken we naar alle aliquot-rijen rijen tot aan 100 (als startgetal) dan is de aliquot-rij startend met 30 de langste: (30,) 42, 54, 66, 78, 90, 144, 259, 45, 33, 15, 9, 4, 3, 1 en heeft een lengte van 14. Gaan we boven de 100 kijken dan krijgen we interessantere rijen. We nemen eens 180. Wanneer we deze aliquot-rij in een grafiek zetten dan krijgen we zoiets als: De grafiek verloopt vrij grillig. Als we naar de grafiek van de aliquot-rij van 498 kijken dan krijgen we: Deze verloopt, op het oog, wat minder grillig dan de vorige maar dat heeft met name te maken dat de meeste sommen (afgezet op de y-as) in elkaar gedrukt zijn. De piek zit namelijk rond de 700.00 (722.961 om precies te zijn). De log, meer specifiek de 10-log (10log of log10) is namelijk een maat voor het aantal cijfers waaruit een getal bestaat. Om precies te zijn: Het aantal cijfers van een getal g is ⌊10log(g)⌋+1. De haken (‘⌊’ en ‘⌋’) om de 10log betekenen: “Afronden naar beneden”. Op de y-as staat nu dus het aantal cijfers van de aliquot-sommen. Tot nog toe zag het er allemaal best vredig uit, maar schijn bedriegt. Het startgetal 840, bijvoorbeeld, levert een monster van een aliquot-rij op met maar liefst 747 aliquot-sommen. En nu is dit aantal nog niet zo groot maar er zijn aliquot-sommen bij met meer dan 30 cijfers: En ondanks dat de 840-rij grote getallen heeft is er kennelijk toch een omslagpunt waardoor de rij weer keurig eindigt met een 1. Wanneer je alle getallen vanaf 2 tot aan 1000 als start getal van een aliquot-rij neemt dan zijn er rijen bij die ogenschijnlijk niet eindigen. Dit geldt voor de getallen: 276, 306, 396 552, 564, 660, 696, 780, 828, 888, 966 en 996. De dik-gedrukte getallen worden de getallen van Lehmer genoemd omdat die meneer dit als eerste heeft ontdekt of in ieder geval als eerste heeft gepubliceerd. De andere getallen maken deel uit van de aliquot-rijen die starten met een getal van Lehmer. De vraag is of deze aliquot-rijen ooit eindigen, en zo ja, hoe. Om één en ander zelf te onderzoeken heb ik een programma in Python gemaakt waarvan hier de code: Code Inleiding
Nee en ja.
Nee, omdat het geen belangwekkende problemen voor de wiskunde zijn.
Ja, omdat de manier van oplossen nieuwe inzichten kan verschaffen voor het oplossen van wel belanghebbende problemen in de wiskunde die dan ook weer gevolgen kunnen hebben voor andere wetenschappen.Priemtweelingen
Onopgelost: Zijn er oneindig veel priemtweelingen?
Volmaakte getallen
28 = 22 × (23 – 1) = 22 × M3,
496 = 24 × (25 – 1) = 24 × M5,
8128 = 26 × (27 – 1) = 26 × M7,
33.550.336 = 212 × (213 – 1) = 212 × M13
(1 + 2 + 4 + 8 + 16) + 31(1 + 2 + 4 + 8 + 16) =
(1 + 31)(1 + 2 + 4 + 8 + 16) =
32 × 31 = 25 × (25 – 1).
(2n – 1) + 21(2n – 1) + 22(2n – 1) + 23(2n – 1) + … + 2n-2(2n – 1) + 2n-1(2n – 1).
(2n-1+1)(1 + 21 + 22 + 23 + … + 2n-2 + 2n-1) =
2n(1 + 21 + 22 + 23 + … + 2n-2 + 2n-1).
2T = 21 + 22 + 23 + … + 2n-2 + 2n-1 + 2n.
T = 1 + 21 + 22 + 23 + … + 2n-2 + 2n-1 + 0
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ -/-
2T – T = -1 + 2n = 2n-1
2n.T = 2n(2n-1).Onopgelost: Zijn er oneven volmaakte getallen?
(als ze er zijn dan zijn ze groter dan 101500)Parker Product Chains
Ketting-lengte
Getal
Ketting-producten
0
0
n.v.t.
1
10
0
2
25
10, 0
3
39
27, 14, 4
4
77
49, 36, 18, 8
5
679
378, 168, 48, 32, 6
6
6.788
2688, 768, 336, 54, 20, 0
7
68.889
27648, 2688, 768, 336, 54, 20, 0
8
2.677.889
338688, 27648, 2688, 768, 336, 54, 20, 0
9
26.888.999
4478976, 338688, 27648, 2688, 768, 336, 54, 20, 0
10
3.778.888.999
438939648, 4478976, 338688, 27648, 2688, 768, 336, 54, 20, 0
11
277.777.788.888.899
4996238671872, 438939648, 4478976, 338688, 27648, 2688, 768, 336, 54, 20, 0
Tot nog toe heb ik alle (in aanmerking komende) getallen tot 10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 (tien octiljoen, zie Nomenclatuur getallen) getest.Onopgelost: Zijn er getallen met een langere product-ketting dan 11 of is 11 het maximum?
Vermoeden van Collatz
Als dit getal even is dan deel je het door 2.
Als dit getal oneven is dan vermenigvuldig je het met 3 en telt er 1 bij op.
n = 11, dan 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1Onopgelost: Is het vermoeden van Collatz waar?
Aliquots
Vrij vertaald: “deel van een groter geheel”.
Onder de echte delers van een getal verstaan we alle delers behalve het getal zelf.
Het wordt pas echt interessant wanneer we naar rijen van aliquots gaan kijken.Aliquot-rijen
De aliquot-rijen van perfecte getallen zijn “het getal zelf” en hebben ook een lengte van 1.
De rij is als volgt: 366, 378, 582, 594, 846, 1026, 1374, 1386, 2358, 2790, 4698, 6192, 11540, 12736, 12664, 11096, 11104, 10820, 11944, 10466, 5236, 6860, 9940, 14252, 14308, 15218, 10894, 6746, 3376, 3196, 2852, 2524, 1900, 2440, 3140, 3496, 3704, 3256, 3584, 4600, 6560, 9316, 8072, 7078, 3542, 3370, 2714, 1606, 1058, 601, 1,
met een lengte van 151.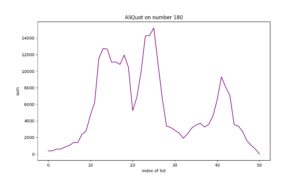
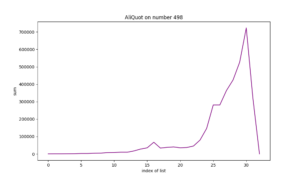
Wanneer de aliquot-sommen uit de hand lopen kunnen we beter een log-grafiek laten zien: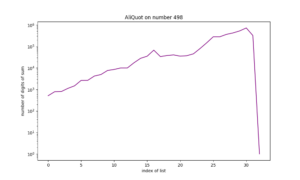
Zo is het aantal cijfers van 99: ⌊10log(99)⌋+1 = ⌊1,99563…⌋+1 = 1+1 = 2 en
het aantal cijfers van 101: ⌊10log(101)⌋+1 = ⌊2,00432…⌋+1 = 2+1 = 3.Monsters
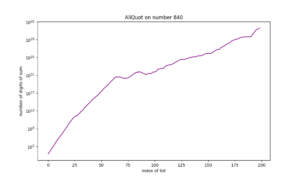
Onopgelost: Eindigt iedere aliquot-rij?
Python programma
Onopgeloste problemen
inv=inv+[a*100+b*10+c
for a in range(2,10)
for b in range (a,10)
for c in range (b,10)
if test(a*100+b*10+c)]
\begin{matrix}a_{0}=n\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\a_{i+1}=\left\{\begin{matrix}\frac{a_{i}}{2}\: als\: a_{i}\: even\: is\\ 3a_{i}+1\: als\: a_{i}\: oneven\: is\end{matrix}\right.\\ \end{matrix}
#Aliquots = deel van een groter geheel (ALIus = anders; QUOT = hoeveel)
#aliquotsom: De som van de echte delers van een getal
#deficient-ontoereikend/gebrekkig als de aliquotsom(n)<n
#abundant-overvloedig/rijk/uitbundig als de aliquotsom(n)>n
#De vijf van Lehmer: getallen onder de 1000 waarvan men niet kan aantonen dat de aliquotrij eindigt
#De vijf van Lehmer: 276, 552, 564, 660, 966
import math
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.animation as animation
import sympy
ar=[]
def correctmarker(marker: str) -> bool:
“””
## correctmarker determines if the marker is accepted for the pyplot.plot function
Determines if the marker is accepted for the pyplot.plot function.
### Args:
– `marker (str)`: the type of the marker.
### Returns:
– `bool`: True if the marker is right otherwise False.
“””
if len(marker) > 1:
return False
if marker == ”:
return True
markers = ‘.,ov^<>12348spP*hH+xXdD|_’
found=False
for i in range(len(markers)):
if marker==markers[i]:
found=True
return found
def correctcolor(color: str) -> bool:
“””
## correctcolor determines if the color is accepted for the pyplot.plot function
Determines if the color is accepted for the pyplot.plot function.
### Args:
– `color (str)`: the color.
### Returns:
– `bool`: True is color is right otherwise False.
“””
colors=[‘blue’, ‘orange’, ‘green’, ‘red’, ‘purple’, ‘brown’, ‘pink’, ‘gray’, ‘olive’, ‘cyan’, ‘black’]
if color in colors:
return True
else:
return False
def aliquotsom(g: int) -> int:
“””
## aliquotsom determines the sum of the true divisors of g
Determines the sum of the true divisors of g.
The true divisors of g are all the divisors except the number itself
### Args:
– `g (int)`: the number of wich the aloquot-sum must be calculated.
### Returns:
– `int`: the aliqout-sum fo number g.
“””
if g<4:
som=1
else:
### PURE PYTHON CODE ###
# delers=set()
# # delers=list()
# w=int(math.sqrt(g)+1)
# # print(w)
# for i in range(2,w+1): #loop vanaf 2 want anders komt g ook in deler-lijst
# if g%i == 0:
# delers.add(i)
# delers.add(g//i)
# # delers.append(i)
# # delers.append(g//i)
# # delers.sort()
# # delers=list(set(delers))
# # print(delers)
# # som=1 #1 is altijd een echte deler van g
# som = 0
# for i in delers:
# som += i
### OPTIMALIZATION WITH SYMPY ###
delers=sympy.divisors(g)
delers.pop()
som = sum(delers)
return som
def aliquotrij(start:int, max: int=70, debug=False):
“””
## aliquotrij makes a list of the aliqout-chain starting with the number start
Makes a list of the aliqout-chain starting with the number start.
Returns the list with the aliquot-numbers and the length of the list.
When the list did not stop after max loops the last item of the list will become -1.
### Args:
– `start (int)`: the start number of the aliquot chain.
– `max (_type_, optional)`: the maximum length of the aliquot-chain. Defaults to None.
– `debug (bool, optional)`: if True: you see a dot after each 5 steps in the loop. Defaults to False.
### Returns:
– `_type_`: the list with the aliquot-numbers and the length of the list.
“””
t=0
hl=[]
door=True
i=start
while door:
t+=1
if debug:
if t%5==0:
print(t, end=”, “, flush=True)
a_s=aliquotsom(i)
# print(a_s)
if a_s==1:
hl.append(1)
door=((a_s!=1) and not(a_s in hl) and (t<max))
if door:
hl.append(a_s)
# print(hl)
i=a_s
if t>=max:
hl.append(-1)
return hl, len(hl)
def bepaal_ar(g: int, max: int=70, show: bool=False):
“””
## bepaal_ar makes the list of the aliquot-chain starting with number g
Makes the list of the aliquot-chain starting with number g.
This function is run only once for efficiency reasons.
### Args:
– `g (int)`: the start number of the aliquot chain.
– `max (int, optional)`: the maximum length of the aliquot-chain. Defaults to 70.
– `show (bool, optional)`: if True: displays the list of the aliquot-chain. Defaults to False.
### Returns:
– `_type_`: the list with the aliquot-numbers and the length of the list.
“””
global ar
if not ar:
ar = aliquotrij(g, max=max)
if show:
print(ar[0])
return ar
def aliquotgraf(g: int, logscale=None, color: str=’blue’, marker: str=’o’, markersize: int=6,
max: int=70, show: bool=False, file_name: str=”) -> None:
“””
## aliquotgraf makes a graph of the aloquot-chain of the number g
Makes a graph of the aloquot-chain of the number g.
### Args:
– `g (int)`: the start number of the aliquot chain.
– `logscale (_type_, optional)`: if equal to ‘log10’ the y-axis will be a log10-scale. Defaults to None.
– `color (str, optional)`: color of the graph. Defaults to ‘blue’.
– `marker (str, optional)`: marker of the graph-points. Defaults to ‘o’.
– `markersize (int, optional)`: the size of the marker. Defaults to 6.
– `max (int, optional)`: the maximum length of the aliquot-chain. Defaults to 70.
– `show (bool, optional)`: if True: displays the list of the aliquot-chain. Defaults to False.
– `file_name (str, optional)`: if set the graph will be saved as png on disk. Defaults to ”.
“””
global ar
if not correctmarker(marker):
marker=’o’
if not correctcolor(color):
color=’blue’
lst=list()
l=0
ar = bepaal_ar(g, max=max, show=show)
lst=ar[0]
if lst[-1] == -1:
lst.pop()
l=ar[1]
plt.figure(figsize=(10,6), num=”AliQuot”)
plt.title(f’AliQuot on number {g}’)
plt.xlabel(‘index of list’)
plt.plot(lst, color=color, marker=marker, markersize=markersize)
# plt.yscale(“linear”)
if logscale == ‘log10’:
plt.yscale(“log”, base=10)
plt.ylabel(‘number of digits of sum’)
else:
plt.ylabel(‘sum’)
# plt.xscale(“linear”)
if len(file_name) > 0:
plt.savefig(f’c:/data/python/data/aliquots/{file_name}.png’)
plt.show()
def aliquotanimation(g: int, logscale=None, color: str=’blue’, marker: str=’o’, markersize: int=6,
interval: int=200, repeat: bool=False, repeat_delay: int=0, max: int=70,
show: bool=False, file_name: str=”) -> None:
“””
## aliquotanimation makes a animated graph of the aliquot-chain of the number g
Makes a animated graph of the aliquot-chain of the number g where the scale of the axes is static.
### Args:
– `g (int)`: the start number of the aliquot chain.
– `logscale (_type_, optional)`: if equal to ‘log10’ the y-axis will be a log10-scale. Defaults to None.
– `color (str, optional)`: color of the graph. Defaults to ‘blue’.
– `marker (str, optional)`: marker of the graph-points. Defaults to ‘o’.
– `markersize (int, optional)`: the size of the marker. Defaults to 6.
– `interval (int, optional)`: the time in ms between the frames. Defaults to 200.
– `repeat (bool, optional)`: if True: the graph will repeat. Defaults to False.
– `repeat_delay (int, optional)`: the time in ms between repeats. Defaults to 0.
– `max (int, optional)`: the maximum length of the aliquot-chain. Defaults to 70.
– `show (bool, optional)`: if True: displays the list of the aliquot-chain. Defaults to False.
– `file_name (str, optional)`: if set the graph will be saved as gif on disk. Defaults to ”.
“””
global ar
if not correctmarker(marker):
marker=’o’
if not correctcolor(color):
color=’blue’
ar = bepaal_ar(g, max=max, show=show)
if ar[0][-1] == -1:
ar[0].pop()
x = np.array(list(range(ar[1])))
y = np.array(ar[0])
fig, ax = plt.subplots(figsize=(10,6), num=”AliQuot: Static axes”)
plt.suptitle(f’AliQuot on number {g}’)
plt.xlabel(‘index of list’)
artists = []
for i in range(ar[1]):
container = ax.plot(x[:i], y[:i], color=color, marker=marker, markersize=markersize)
artists.append(container)
if logscale == ‘log10’:
plt.yscale(“log”, base=10)
plt.ylabel(‘number of digits of sum’)
else:
plt.ylabel(‘sum’)
ani = animation.ArtistAnimation(fig=fig, artists=artists, interval=interval, repeat=repeat, repeat_delay=repeat_delay, blit=False)
if len(file_name) > 0:
ani.save(f’c:/data/python/data/aliquots/{file_name}.gif’, writer=’pillow’, fps=60)
plt.show()
maxi: int = -1
def aliquotanimation_dynamic(g: int, logscale=None, color: str=’blue’, marker: str=’o’, markersize: int=6,
interval: int=200, repeat: bool=False, repeat_delay: int=0, max: int=70,
show: bool=False, file_name: str=”) -> None:
“””
## aliquotanimation_dynamic makes a animated graph of the aliquot-chain of the number g
Makes a animated graph of the aliquot-chain of the number g where the scale of the axes is dynamic.
### Args:
– `g (int)`: the start number of the aliquot chain.
– `logscale (_type_, optional)`: if equal to ‘log10’ the y-axis will be a log10-scale. Defaults to None.
– `color (str, optional)`: color of the graph. Defaults to ‘blue’.
– `marker (str, optional)`: marker of the graph-points. Defaults to ‘o’.
– `markersize (int, optional)`: the size of the marker. Defaults to 6.
– `interval (int, optional)`: the time in ms between the frames. Defaults to 200.
– `repeat (bool, optional)`: if True: the graph will repeat. Defaults to False.
– `repeat_delay (int, optional)`: the time in ms between repeats. Defaults to 0.
– `max (int, optional)`: the maximum length of the aliquot-chain. Defaults to 70.
– `show (bool, optional)`: if True: displays the list of the aliquot-chain. Defaults to False.
– `file_name (str, optional)`: if set the graph will be saved as gif on disk. Defaults to ”.
“””
global ar
if not correctmarker(marker):
marker=’o’
if not correctcolor(color):
color=’blue’
ar = bepaal_ar(g, max=max, show=show)
s = 0
if ar[0][-1] == -1:
ar[0].pop()
s = 1
x = np.array(list(range(len(ar[0]))))
y = np.array(ar[0], dtype=float)
fig, ax = plt.subplots(figsize=(10,6), num=”AliQuot: Dynamic axis”)
plt.suptitle(f’AliQuot on number {g}’)
plt.xlabel(‘index of list’)
ax.plot(x, y, color=color, marker=marker, markersize=markersize)
def animate(num, y):
global maxi
# print(num)
if y[num] > maxi:
maxi = y[num]
if logscale == ‘log10’:
ax.set_ylim(bottom=1, top=maxi)
else:
ax.set_ylim(bottom=-1, top=maxi)
ax.set_xlim(left=0, right=num+1)
if logscale == ‘log10’:
plt.yscale(“log”, base=10)
plt.ylabel(‘number of digits of sum’)
else:
plt.ylabel(‘sum’)
ani=animation.FuncAnimation(fig, animate, frames=len(x), repeat=repeat, repeat_delay=repeat_delay, fargs=[y], interval=interval)
if len(file_name) > 0:
ani.save(f’c:/data/python/data/aliquots/{file_name}.gif’, writer=’pillow’, fps=60)
plt.show()
import time
# examples
# print(aliquotsom(36))
# st0=time.time()
# ar=aliquotrij(990, 750, debug=True)
# st1=time.time()
# print(ar[0], ar[1])
# print(st1-st0)
# show aliquotrij for range of numbers
# for i in range(501,601):
# ar = aliquotrij(i, 250)
# print(f'{i:3}: {ar[0]}; len={ar[1]}’)
# show (and save) different static and dynamic graphs
number = 498
# number = 840
aliquotgraf(g=number, max=200, logscale=’log10′, marker=”, color=’purple’, file_name=f'{number}_l’, show=True)
aliquotgraf(g=number, max=200, logscale=None, marker=”, color=’purple’, file_name=f'{number}’, show=True)
aliquotanimation(g=number, logscale=’log10′, marker=”, color=’purple’, interval=2,
repeat=False, repeat_delay=1000, max=200, show=True, file_name=f'{number}_sl’)
aliquotanimation_dynamic(g=number, logscale=’log10′, marker=”, color=’purple’, interval=2,
repeat=False, repeat_delay=1000, max=200, show=True, file_name=f'{number}_dl’)
aliquotanimation(g=number, logscale=None, marker=”, color=’purple’, interval=2,
repeat=False, repeat_delay=1000, max=200, show=True, file_name=f'{number}_s’)
aliquotanimation_dynamic(g=number, logscale=None, marker=”, color=’purple’, interval=2,
repeat=False, repeat_delay=1000, max=200, show=True, file_name=f'{number}_d’)