Inhoud
Op YouTube kwam ik, na getipt te zijn, het volgende filmpje tegen: 3-4-5 Triangles and Pi. Het gaat over de oppervlakte van de ingeschreven cirkel in een Pythagorese 3-4-5-driehoek. Het verrassende antwoord blijkt pi (π) te zijn. En hoewel de maker (Andy Math) een keurige uitleg geeft gaat hij wel vlug over alle stappen heen. In dit artikel zal ik de stappen wat uitgebreider behandelen waarna ik ook een veralgemenisering van dit fenomeen geef. Dus niet alleen voor 3-4-5 driehoeken maar voor alle Pythagorese driehoeken. En ook dit levert weer een verrassend resultaat op. Maar voor we in de diepte stappen eerst wat basisbegrippen; dit zijn begrippen waarvan ik geen bewijs zal leveren. Hieronder som ik wat basisbegrippen op die u vast al weet. Natuurlijk getal: Een positief geheel getal (als het uitkomt mag 0 ook meedoen). Cirkel: Op een cirkel liggen alle punten met dezelfde afstand tot 1 punt; dat punt wordt middelpunt genoemd. Vierhoek: Een aaneengesloten figuur met 4 rechte lijnen waarvan de hoeken bij elkaar opgeteld 360º bedragen. Driehoek: Een aaneengesloten figuur van 3 rechte lijnen waarvan de hoeken bij elkaar 180º bedragen. Rechthoekige driehoek: Een driehoek waarvan 1 van de hoeken precies 90º bedraagt. De schuine zijde wordt hypotenusa genoemd, de 2 andere zijden worden de rechthoekszijden genoemd. De som van de rechthoekszijden is groter dan de hypotenusa. Pythagorese driehoek: Een rechthoekige driehoek waarvan de zijden allemaal natuurlijke getallen zijn. Gelijkbenige driehoek: Een driehoek met 2 even grote zijden. De basishoeken zijn dan gelijk. Ingeschreven cirkel: Een cirkel in een veelhoek die alle zijden van de veelhoek raakt. Verder geldt dat de lijn vanuit het middelpunt naar een raakpunt (de straal dus) loodrecht staat op de raaklijn aan dat raakpunt. Stelling: De 2 raaklijnen aan een cirkel vanuit een punt buiten de cirkel hebben dezelfde lengte. Bekijk het onderstaande plaatje: Hier is een cirkel c met middelpunt M. Verder een punt A dat buiten de cirkel ligt. Vanuit A zijn twee raaklijnen, f en g, naar de cirkel getekend. Raaklijn f raakt de cirkel in raakpunt D en raaklijn g raakt de cirkel in raakpunt C. Bewijs: We moeten bewijzen dat de lengte van punt A tot punt D gelijk is aan de lengte van punt A tot punt C. In de wiskunde schrijven we dit wat korter. We moeten dus bewijzen dat |AC| = |AD|. Vanuit M trekken we 2 lijnen naar respectievelijk C en D: De lijnen |MC| en |MD| zijn natuurlijk de straal van de cirkel. Deze stralen staan loodrecht op f en g: We kunnen nu dus concluderen dat |MC| = |MD| en dat ∠ACM = ∠ADM = 90º (∠ betekent hoek). Trekken we vervolgens de het lijnstuk |CD|: Dan kunnen we de conclusie trekken dat ΔCDM een gelijkbenige driehoek is, want |MC| = |MD. Laten we nu eens naar de basishoeken van ΔCDM kijken: Hier geldt dus dat ∠DCM = ∠CDM ( de roze stippeltjes). Kijken we nu naar de “overblijvende” hoeken (blauwe stippeltjes): Dan geldt dat: Dus ∠ACD = ∠ADC (de blauwe stippeltjes). Maar dan geldt dat ΔACD gelijkbenig is en dat betekent dat |AC| = |AD|. q.e.d. Stelling: De oppervlakte van de ingeschreven cirkel in de Pythagorese 3-4-5-driehoek is π. Bekijk het onderstaande plaatje: Hier zien we de situatie zoals in de stelling staat beschreven: We hebben de ΔABC met |AB| = 3, |BC| = 4 en |AC| = 5. Verder de ingeschreven cirkel met middelpunt M. We trekken nu de lijnstukken |ME| en |MF|: De lijnstukken |ME| en |MF| zijn de stralen van de cirkel en noemen we r. Omdat de straal van een ingeschreven cirkel loodrecht staat op de raaklijn naar het raakpunt geldt: ∠BEM = 90º en ∠BFM = 90º. Omdat ΔABC een rechthoekige driehoek is geldt ook: ∠ABC = 90º: Maar omdat alle hoeken van een vierhoek bij elkaar opgeteld 360º bedragen is ∠EMF = 360º – ∠BEM – ∠BFM – ∠ABC = 360º – 90º = 90º – 90º = 360º – 270º = 90º. Vierhoek BFME is dus een vierkant. En van een vierkant zijn alle zijden even groot, dus: |BF| = |FM| = |ME| = |BE| = r: Maar dit betekent nu dat |AB| = 3 = r + |EA| en dus |EA| = 3 – r. Hetzelfde geldt voor |BC| = 4 = r + |FC| en dus |FC| = 4 – r: Maar uit Stelling 1 volgt nu dat |AE| = |AG| = 3-r en |CF| =|CG| = 4-r: En met al deze gegevens kunnen we nu r gaan uitrekenen: 3-r + 4-r = 5 → 7 – 2r = 5 → -2r = -2 → r=1. De straal is dus 1 en dan is de oppervlakte van de cirkel dus: π.r2 = π.12 = π. q.e.d. Stelling: De oppervlakte van een ingeschreven cirkel in een Pythagorese driehoek is een natuurlijk veelvoud van π. Bekijk eerst weer onderstaande figuur: Hierin zijn de 3, 4 en 5 vervangen door respectievelijk a, b en c. Het bewijs verloopt geheel analoog aan het bewijs van Stelling 2, alleen de laatste berekening wordt nu: En omdat in een Pythagorese driehoek de zijden allemaal natuurlijke getallen zijn is c-b-a een negatief geheel getal, daar de som van de rechthoekszijden (a+b) groter is dan de hypotenusa(c). Verder geldt dat of a of b oneven is en de andere even is en c ook oneven is (zie Pythagorese drietallen). Dit betekent dat het verschil tussen een even getal en een oneven getal ook oneven is en het verschil tussen een oneven getal en een oneven getal weer even is. Dus is c-b-a deelbaar door 2 en dus ook door -2. En omdat c-b-a kleiner dan 0 is, is (c-b-a)\-2 een positief geheel getal. En dit betekent dat de oppervlakte van de cirkel een natuurlijk veelvoud van π is. q.e.d. Opmerking: Dat “natuurlijke veelvoud” is ook een geheel kwadraat. Dat is logisch want dat komt voort uit de formule van de oppervlakte van een cirkel met straal r: πr2. Uit de berekening van het bewijs van stelling 3 hebben we nu ook een formule voor de oppervlakte van een ingeschreven cirkel in een Pythagorese driehoek, namelijk: Dus de oppervlakte van een 5-12-13 Pythagorese driehoek is ((13-12-5))2/-2×π = (-4/-2)2×π = (-2)2×π = 4π. YouTube: 3-4-5 Triangles and Pi Inleiding
Basisbegrippen
De oppervlakte van een cirkel is π.r2, waarbij r de straal (afstand van middelpunt tot een punt op de cirkel) is en π≈3.14159265… is.Stelling 1
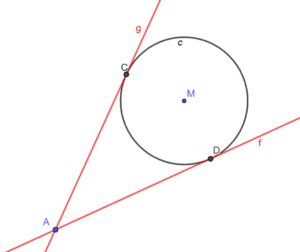
De lengte van een lijnstuk van punt X naar punt Y noteren we als: |XY|.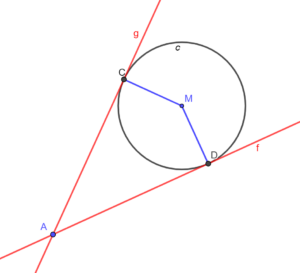
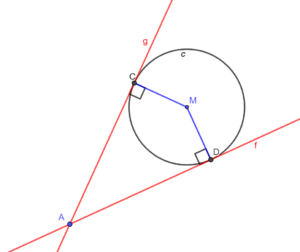
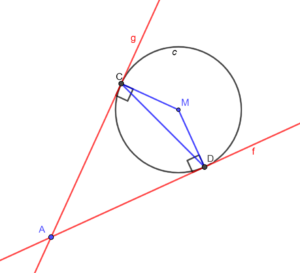
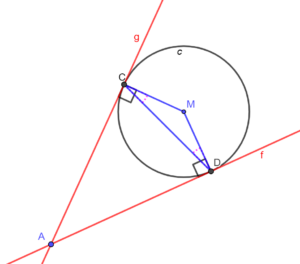
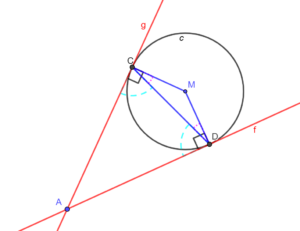
∠ACD = 90º – ∠DCM = 90º – ∠CDM, en
∠ADC = 90º – ∠CDM = 90º – ∠DCM.Stelling 2
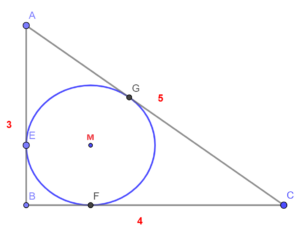
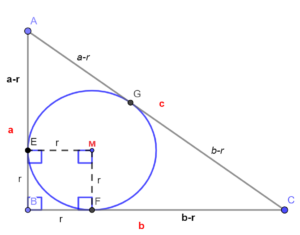
Verder zijn de lijnstukken |AB|, |BC| en |AC| de raaklijnen aan cirkel met respectievelijk de raakpunten E, F en G.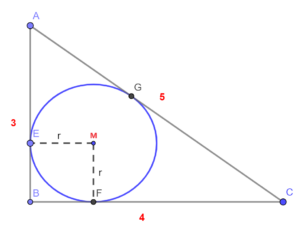
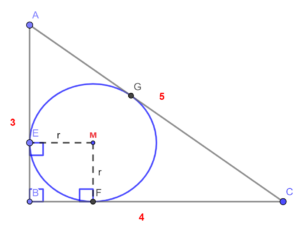
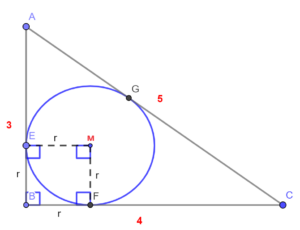
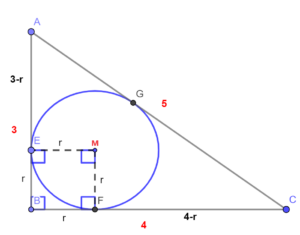
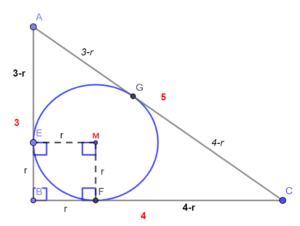
Stelling 3
Dit betekent dat c-b-a is “oneven”-(“oneven”-“even”)=”oneven”-“oneven”=”even”.Gevolg
Bron
Pi Thagoras
a\text{ - }r+b\text{ - }r=c\rightarrow \text{ - }2r=c\text{ - }b\text{ - }a\rightarrow r=\frac{c\text{ - }b\text{ - }a}{\text{ - }2}
oppervlakte=\pi \times \left ( \frac{c\text{ - }b\text{ - }a}{\text{ - }2} \right )^{2}