De wet van Benford

De wet van Benford is eigenlijk de wet van Newcomb en gaat over de distributie van begincijfers in data.

Simon Newcomb (12 maart 1835 – 11 juli 1909) was een Canadees-Amerikaanse astronoom. Voor zijn berekeningen raadpleegde hij vaak logaritmische tabellen in een daarvoor bestemd boek. Hij bemerkte dat de eerste pagina’s duidelijk vaker waren gebruikt dan de pagina’s die erna kwamen. Hij had de geniale gedachte dat dit te maken moest hebben met de begincijfers van de getallen waarmee hij werkte en dat dit zou gelden voor veel andere verzamelingen. Ondanks dat Newcomb zijn observatie deelde was het een artikel van Frank Benford die bekendheid gaf aan deze wetmatigheid en heeft dan ook zijn naam gekregen.

Frank Benford (1881 – 4 december 1948) was een Amerikaans ingenieur en natuurkundige en kwam met een mooie formule voor de verdeling van begincijfers in allerlei verschillende data.

 

 

De wet van Benford kan gepostuleerd worden als de kans dat een getal uit een verzameling begint met het cijfer d ∈ [1;9].
De formule luidt: P(d) = ¹⁰log(1 + 1/d).

Dit levert de volgende verdeling op:

Cijfer	Kans
1	30,1%
2	17,6%
3	12,5%
4	9,7%
5	7,9%
6	6,7%
7	5,8%
8	5,1%
9	4,6%

Nu is het zo dat deze wetmatigheid (tot nog toe) niet bewezen kan worden en dus alleen (emperisch) kan worden aangetoond door naar verschillende voorbeelden te kijken.

Voorbeelden

De nu volgende voorbeelden zijn allemaal gemaakt in Excel met de wizard Benford uit de add-in HJGSoft-Handigheidjes. Daar waar nodig of nuttig zal ik ook (een deel van) de data laten zien en de onderliggende formules.

Het aantal inwoners van de verschillende Nederlandse gemeenten voldoen aan de wet:

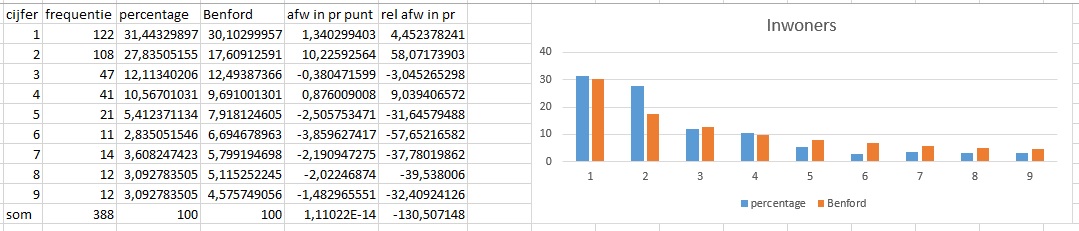
De wizard Benford wil als invoer de reeks met data hebben. Hierna toont de wizard een tabel met de tellingen en daarnaast een verdelings-grafiek. In dit voorbeeld zijn het aantal inwoners van 388 gemeenten geanalyseerd en je ziet dat de begincijfers van het aantal inwoners redelijk goed de wet van Benford volgt. Dit blijkt ook uit de grafiek: De blauwe staafjes (begincijfers inwoners) zijn bijna overal even hoog als de oranje staafjes (ideale Benford verdeling).

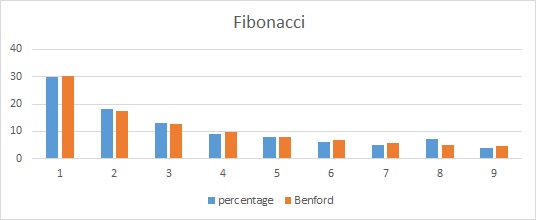
De rij van Fibonacci (1 1 2 3 5 8 13 …; n_e-term=(n-1)_e-term + (n-2)_e-term) voldoet hier ook aan:

En zo ook de opeenvolgende machten van 2 (dus 2⁰=1, 2¹=2, 2²=4, 2³=8, …):

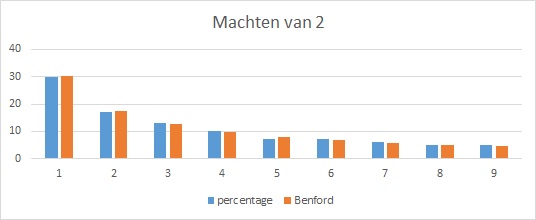
In het sheet heb ik deze machten als een reeks van 10×10 cellen gemaakt vanaf cel A13, dus A13:J22. In cel A13 wil ik dus een 0 als exponent hebben en in cel A14 wil ik 1 als exponent hebben tot aan cel J22 waar ik 99 als exponent wil hebben. Uiteraard wil ik dit niet handmatig intikken maar gebruik maken van een formule (=2^…). Excel kent de functies RIJ en KOLOM. Met de functie RIJ(cel) krijg je het nummer van de rij en met de functie KOLOM(cel) krijg je het nummer van de kolom (met kolom A = 1). De exponenten krijg je nu met de formule: (RIJ(A13)-13)*10+KOLOM(A13)-1. Merk op dat bij deze functies geen kringverwijzing optreedt.

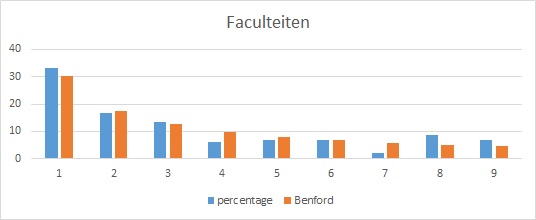
De opeenvolgende faculteiten (3!=1 x 2 x 3=6, n!=1 x 2 x … x n-1 x n) voldoet er ook aan:

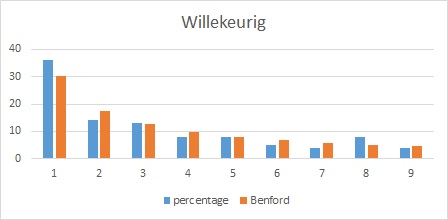
Ogenschijnlijke willekeur blijkt ook vaak te voldoen aan de wet:

Een reeks van 100 willekeurige getallen gemaakt met de formule: =GEHEEL((9*ASELECT()+1)*(9*ASELECT()+1)*(9*ASELECT()+1)*(9*ASELECT()+1)) voldoet:

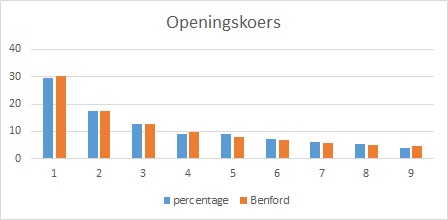
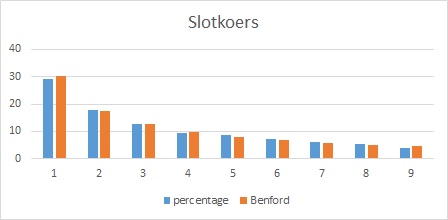
En wat te denken van de openings- en slotkoersen van de New York Stock Exchange:

Invariantie

De vraag is of de wet gevoelig is voor verschillende maatgevingen of niet. Ook dit moet weer emperisch worden vastgesteld.

Laten we als voorbeeld eens kijken naar de oppervlakte van de verschillende Nerderlandse gemeenten:

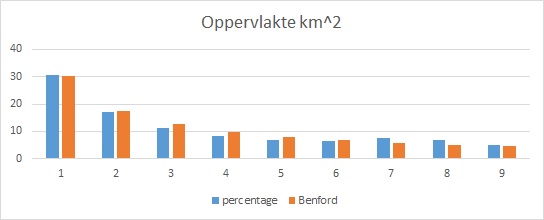
In vierkante-kilometers voldoet dit aan de wet. Maar hoe ziet de grafiek eruit als we de oppervlakte in vierkanten-mijlen hebben:

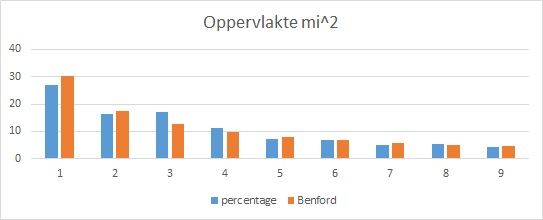
En ook dan ziet het er aardig uit.

Tot nog toe lijkt het erop dat iedere verzameling (mits groot genoeg) voldoet aan de wet. Dit is echter geenszins het geval.

Non-voorbeelden

Hoe mooi sommige wiskundige formules, grootheden, rijen etc. ook aan de wet gehoorzamen zijn er ook die dat absoluut niet doen.

Wat te denken van de sinus en cosinus (op het interval 0-360 graden):

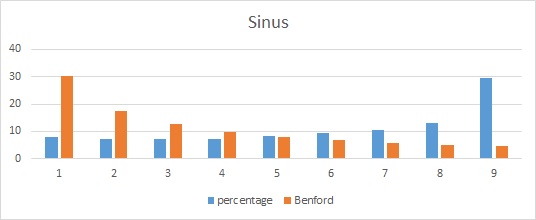
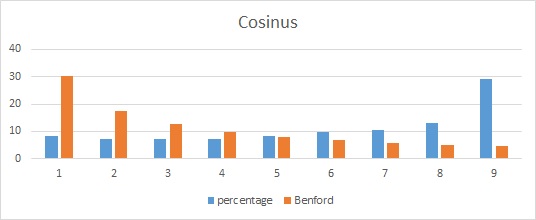
De tangens daarentegen:

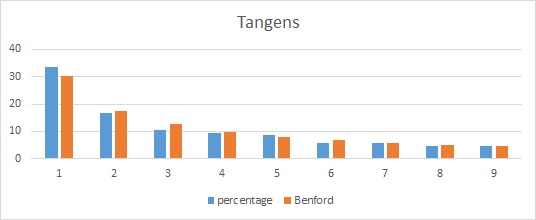
En wat te denken van het gemiddelde inkomen van de bewoners van de Nederlandse gemeenten:

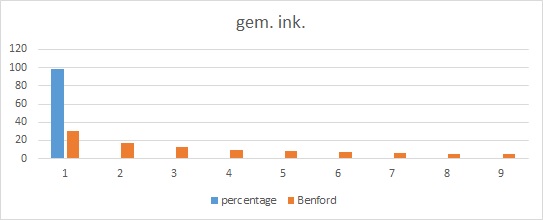
Geldt de verdeling ook voor andere posities?

Het antwoord is ja, maar de berekening wordt iets lastiger, omdat de eerste positie ook in overweging moet worden genomen. Je krijgt dus een som van kansen.

Wat is de kans dat het cijfer 2 op de 2e positie staat. De mogelijkheden zijn dan dus 12…, 22…, 32…, t/m 92… Die kans is ¹⁰log(1+1/12) + ¹⁰log(1+1/22) + ¹⁰log(1+1/32) + … + ¹⁰log(1+1/92) ≈ 0,11.

In z’n algemeenheid geldt:

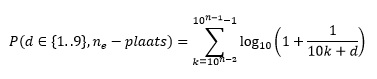
Geldt de verdeling ook voor andere talstelsels?

Ook hier geldt het antwoord ja. In de formule verandert alleen het grondtal van de logaritme. De deler houd je gewoon decimaal.

Dus de kans dat een binair getal begint met 1001 (=9 decimaal) is P(1,0,0,1)=²log(1+1/9)≈0,15.

Zijn er praktische toepassingen?

Jazeker, maar of iedereen daar blij van wordt…

De boekhouding van een bedrijf voldoet ook aan de wet van Benford, mits er niet met de boekhouding is geknoeid. Wanneer iemand met de cijfers rommelt is hij/zij geneigd om een uniforme verdeling van begincijfers aan te houden en dat is dus in tegenspraak met de wet. Hierdoor is door middel van een Benford-analyse fraude aan het licht te brengen. En er zijn inmiddels rechtzaken bekend waar door middel van de Benford-analyse fraude bewezen is geacht.

Geraadpleegde sites

https://nl.wikipedia.org/wiki/Wet_van_Benford
https://en.wikipedia.org/wiki/Benford%27s_law
https://en.wikipedia.org/wiki/Simon_Newcomb
https://en.wikipedia.org/wiki/Frank_Benford