Inhoud
Inleiding
Bovenstaande vergelijking is wellicht de mooiste uit de wiskunde. Het combineert twee (bewezen) transcendente (zie Appendix D) getallen, e en π, het imaginaire getal i en het laagste en hoogste getal uit de rekenkunde samen.
Het wordt ook wel de formule van Euler genoemd naar de beroemde Zwitserse wiskundige Leonhard Euler (1707-1783).
In dit artikel doe ik uit de doeken hoe deze formule “gemaakt” kan worden.
Introductie
rekenkunde
In de rekenkunde, een onderdeel van de wiskunde, is 1 het laagste getal omdat ieder (natuurlijk) getal gedeeld kan worden door 1 zonder dat het getal zelf verandert.
In diezelfde rekenkunde is 0 het hoogste getal omdat geen enkel (natuurlijk) getal door 0 kan worden gedeeld.
cirkel
Het getal π (Griekse letter pi) is wel bekend en is de constante die ontstaat wanneer je de omtrek van een cirkel deelt door de diameter van de cirkel. Het blijkt dat π ≈ 3,14159265.
Euler
Het getal e, het getal van Euler (vandaar de e), is de constante met de volgende eigenschap:
f(x) = ex ↔ f’(x) = ex, ofwel de afgeleide van f(x) is precies gelijk aan f(x) zelf!
De officiële definitie van e luidt:
e=\lim_{n\rightarrow \infty}(1+\frac{1}{n})^{n}=\sum_{k=1}^{n}\frac{1}{k!}
Als we in de bovenstaande definitie uitgaan van de som (sigma) dan krijgen we de volgende termen: 1 + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + … = 1 + 1 + 1/2 +1/6 + 1/24 + 1/120 + … ≈ 2,718281828.
faculteit
Het uitroepteken achter een getal betekent in de wiskunde de faculteit van dat getal en is niets anders dan de vermenigvuldiging van 1 x 2 x 3 x… x het getal. Dus 5! = 1 x 2 x 3 x 4 x 5 = 120.
De betekenis van faculteit kan gevonden worden in de kansberekening. Het beantwoordt de vraag op hoeveel verschillende manieren je n voorwerpen kunt rangschikken.
Dus als je 5 pennen hebt: Op hoeveel verschillende manieren kun je die dan op een rijtje leggen? Het antwoord is op 5! = 120 verschillende manieren.
imaginair getal
Tot slot het getal i; het zogenaamde imaginaire getal (natuurkundigen gebruiken meestal de letter j). Het getal i is een getal met de volgende eigenschap: i2 = -1.
Het getal zorgt er bijvoorbeeld voor dat iedere (polynomiale) vergelijking in de wiskunde een oplossing heeft.
Wanneer je bijvoorbeeld kijkt naar de vergelijking x2 – 4 = 0 dan krijg je x2 = 4 en dus x = 2 of x = -2.
Kijk je nu bijvoorbeeld naar de vergelijking x2 + 4 = 0 dan krijg je x2 = -4. En op de middelbare school heb je geleerd dat je geen wortel van een negatief getal kunt trekken. Maar met de introductie van i kan dat nu wel. De oplossing van de laatste vergelijking is nu x = 2i of x = ‑2i. Ga maar na: x = 2i dan x2 = (2i)2 = 4i2 en omdat i2 = -1 krijg je dus 4i2 = 4 x -1 = -4. Hetzelfde geldt voor x = -2i.
Poolcoördinaten
Op de middelbare school heb je kennis gemaakt met het (Cartesisch, vernoemd naar René Descartes) assenstelsel. Dit zijn twee haaks op elkaar staande rechte lijnen. De horizontale lijn noem je de x-as en de verticale lijn noem je de y-as. Ieder punt in dit vlak kan nu op unieke wijze gekenmerkt worden door de x-coördinaat en de y-coördinaat; (x, y).
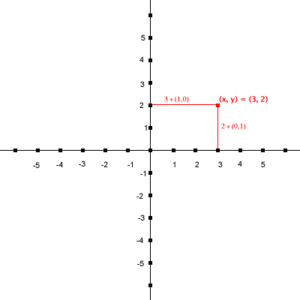
Zo heeft het rode punt in Figuur 1 de coördinaten (3, 2) wat betekent dat je vanaf het kruispunt van de x-as en de y-as, de oorsprong genaamd, 3 stappen naar rechts gaat en 2 stappen naar boven.
Nu kun je datzelfde punt ook op een andere, eenduidige, manier beschrijven.
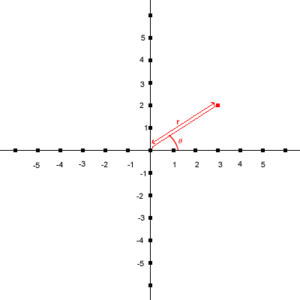
In Figuur 2 wordt het rode punt beschreven door de grootte van de lijn vanaf de oorsprong tot het punt (r) en de (positieve) hoek die die lijn maakt met de x-as (θ, Theta).
Het punt ligt dus vast als (r, θ).
De lengte r wordt ook wel modulus of absolute waarde genoemd en θ het argument.
Maar hoe komen we nu van Cartesische coördinaten naar poolcoördinaten?
Welnu, dat is niet heel moeilijk.
Om r te bepalen gebruik je de stelling van Pythagoras: x2 + y2 = r2.
In Figuur 1 hadden we het punt (3, 2). Dus de lengte van de lijn vanaf de oorsprong (0, 0) tot aan het punt (3, 2) is: r = √(32 + 22) = √(9 + 4) = √13.
Het argument is niets anders dan de inverse tangens van de driehoek ABC met A = (0, 0), B = (3, 0) en C = (3,2) en dus θ = tan-1(2/3) » 33,7°.
Het punt in Figuur 2 is dus (√13, 33,7°).
Omgekeerd, dus van poolcoördinaten naar Cartesische coördinaten gebruik je de volgende formules:
x = rcos(θ) en y = rsin(θ), want de cos(θ) is de aanliggende zijde gedeeld door de schuine zijde, dus x/r en de sin(θ) is de overstaande zijde gedeeld door de schuine zijde, dus y/r.
Met poolcoördinaat-vergelijkingen kun je hele mooie grafieken maken:
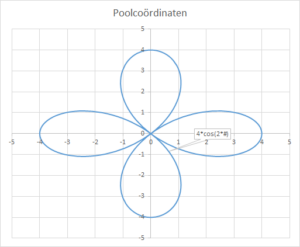
In Figuur 3 is de grafiek van de vergelijking f(h) = 4cos(2h) getekend waarbij 0 ≤ h ≤ 2π.
Maar de echte reden van dit onderdeel komt terug in het volgende onderdeel.
Complexe getallen
Zoals eerder genoemd zijn imaginaire getallen gebaseerd op het getal i met de eigenschap i2 = -1.
Een complex getal is een getal van de volgende vorm: z = a + bi, waarbij a en b reële getallen zijn. Het getal a is het reële deel van het complexe getal, Re(z), en bi het imaginaire deel van het getal, Im(z).
Alle complexe getallen zitten in de verzameling ℂ. Dit is een uitbreiding van de verzameling ℝ, waarin alle reële getallen zitten, met alle complexe getallen.
We kunnen een complex getal weergeven in een Cartesisch assenstelsel waarbij we de x-as vervangen door de reële as en de y-as door de imaginaire as.
Dus een complex getal z = a + bi heeft in het assenstelsel de coördinaten (a, bi).
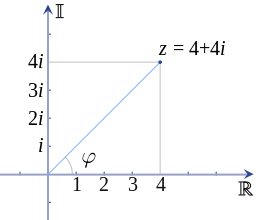
In Figuur 4 zie je het punt z = 4 + 4i afgebeeld.
En nu komt het mooie. We kunnen complexe getallen en poolcoördinaten gaan combineren.
Wanneer z = a + bi dan kunnen we a uitdrukken als a = rcos(θ) en bi als bi = risin(θ) en aldus z als z = rcos(θ) + risin(θ) = r(cos(θ) + isin(θ)).
Differentiëren
Differentiëren (zie Appendix C) is in de wiskunde een techniek om de richtingscoëfficiënt van de raaklijnen aan een grafiek te bepalen.
Voorbeeld:
Stel we hebben de functie f(x) = x2. Als we de afgeleide (zo wordt differentiëren ook genoemd) van f(x) bepalen dan krijgen we f’(x) = 2x. Dit betekent dat als we de raaklijn willen bepalen in het punt 2 van de grafiek deze raaklijn een richtingscoëfficiënt van f’(2) = 2 x 2 = 4 heeft.
Als we de vergelijking van de raaklijn in punt 2 willen hebben dan krijgen we de vergelijking y = 4x – 4.
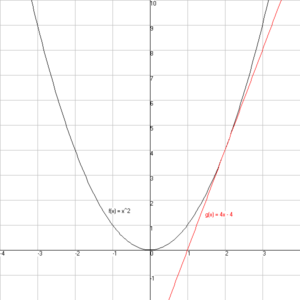
In Figuur 5 is bovenstaand voorbeeld uitgewerkt.
Nu vroeg Euler (eigenlijk eerst Napier; de “uitvinder” van de logaritme (zie Appendix A)) zich af of er ook een functie bestaat waarvan de afgeleide functie gelijk is aan de functie zelf.
Hij zocht naar een functie f(x) = ax waarvan f’(x) = ax is.
Om in z’n algemeenheid de afgeleide van een functie f(x) te bepalen maak je gebruik van de volgende formule:
f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)\text{ - }f(x)}{h}
En deze (limiet-; zie Appendix B) formule wordt gebruikt om de afgeleide van f(x) = ax te bepalen voor bepaalde a zodanig dat de afgeleide precies ax oplevert.
En via een tabelletje laat ik zien hoe we aan a komen:
| a [f(x)=ax] |
f’(x) |
| 2,5x |
2,5x x 0,916 |
| 2,6 x |
2,6 x x 0,955 |
| 2,7 x |
2,7 x x 0,993 |
| 2,8 x |
2,8 x x 1,029 |
| 2,75 x |
2,75 x x 1,011 |
| 2,725 x |
2,725 x x 1,002 |
| 2,715 x |
2,715 x x 0,999 |
De kunst is dus om de factor achter ax gelijk aan 1 te krijgen.
Euler ontdekte dat a dan 2,718281828904590… moet zijn. En dat is dus het getal van Euler die we e noemen!
Een logaritme met grondtal e wordt dan ook de natuurlijke logaritme genoemd en wordt als ln genoteerd.
Overigens is de formule voor de afgeleide van f(x) = ax, f’(x) = ax.ln(a). En in het geval dat a = e is ln(a) = ln(e) = 1.
Opmerking: Het getal e is eerder ontdekt door Jacob Bernoulli bij zijn berekeningen naar samengesteld interest: €1x(1+1/∞)∞=€2,714281428459045…=€e.
Slot
Laten we nu eens al het voorgaande op een slimme manier gaan combineren.
goniometrie
Een paar wetenswaardigheden over goniometrie zullen we hier herhalen.
Als f(x) = cos(x) dan f’(x) = -sin(x).
Als f(x) = sin(x) dan f’(x) = cos(x).
Een hoek van 180° = π.
Sin(180°) = sin(π) = 0.
Cos(180°) = cos(π) = -1.
We weten dat we z = a + bi kunnen schrijven als z = r(cos(θ) + isin(θ)). Laten we voor het gemak eens r = 1 kiezen en dan de volgende functie gaan differentiëren:
f(x) = cos(x) + isin(x)
f’(x) = -sin(x) + icos(x) = i(cos(x) + isin(x)), en wat nu als laatste tussen haakjes staat is weer f(x).
Dus f’(x) = i.f(x). En buiten het feit dat i hier gewoon een constante is hebben we hier een functie waarvan de afgeleide weer dezelfde functie oplevert.
En we weten dat er nog zo’n functie bestaat, namelijk f(x) = f’(x) = ex.
Alleen missen we nog de factor i voor de f(x).
Wat als f(x)=eix? Dan is f’(x) = ieix = i.f(x) (toepassen van de kettingregel).
En daar is onze factor i.
We mogen dus f(x) = cos(x) + isin(x) ook schrijven als f(x) = eix.
Dus f(x) = cos(x) + isin(x) = eix.
Stel dat we nu voor x het getal π invullen.
Dan krijgen we dus f(π) = eπi = cos(π) + isin(π) = -1 + i.0 = -1.
Dus eπi = -1 en dus eπi + 1 = 0.
Hoe mooi toch is de wiskunde!!!
Appendix A – Logaritmen
Wanneer je wel eens hebt gerekend dan weet je dat iedere bewerking ook een tegenstelde bewerking heeft.
De tegengestelde bewerking van optellen is aftrekken en de tegengestelde bewerking van vermenigvuldigen is delen.
Maar hoe zit dat nu met machtsverheffen?
Bij machtsverheffen heb je twee tegengestelde bewerkingen. De eerste, en meest bekende, is worteltrekken en levert je het grondtal van de machtsverheffing op.
De tweede levert je de exponent op en dat is logaritme.
Dus een logaritme is niets anders dan een exponent.
Voorbeeld:
We kijken naar de machtsverheffing 210 = 1024. Het getal 2 noemen we het grondtal, het getal 10 de exponent en het getal 1024 het antwoord of resultaat.
Wanneer ik vanuit 210 = 1024 de 2, het grondtal, weer terug wil hebben dan trek ik de 10e‑machts wortel uit 1024, dus:
\sqrt[10]{1024}=2
Maar als ik de exponent, in ons voorbeeld 2, als resultaat wil hebben dan moet ik een logaritme gebruiken. Ik neem dan, in woorden, de “2-log van 1024”.
In symbolen is dat: 2log 1024 = 10 of, wat moderner, log2 1024 = 10.
Dus algemeen: grondtallog antwoord = exponent.
Om een logaritme uit het hoofd te berekenen, of desnoods op papier, is erg bewerkelijk. Daarom is een rekenmachine erg handig. Alleen zit er op een rekenmachine geen 2log, maar enkel de knop log en soms ook de knop ln.
De knop log rekent de 10log uit en de knop ln de natuurlijke logaritme(dus met grondtal e).
Nu is er gelukkig een makkelijke formule om van een nlog een 10log of ln te maken.
Deze luidt:
^{n}\log a=\frac{^{10}\log a}{^{10}\log n}=\frac{\ln a}{\ln n}
Dus om 2log 1024 uit te rekenen toets je op je rekenmachine ln1024/ln2 in.
Appendix B – Limieten
In het stuk hierboven en in Appendix C wordt gesproken over limieten (lim).
Zonder een diepgaande verhandeling hierover te geven beperk ik mij tot een “globale” schets van wat een limiet is.
Er zijn functies waarvan een bepaalde waarde niet bestaat maar waarvan we wel kunnen bepalen wat de functiewaarde moet zijn.
Dit geldt bijvoorbeeld voor functies die een noemer hebben waarvan de waarde 0 kan worden en je kunt nu eenmaal niet delen door 0.
Voorbeeld:
Bekijk de functie:
f(x)=\frac{x^{3}\text{ - }3x^{2}}{x\text{ - }3}
De waarde f(3) bestaat niet omdat x-3 dan 0 wordt.
Kijken we echter naar de grafiek van f(x) dan zien we een “gewone” parabool:
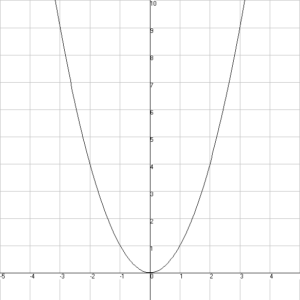
We kunnen nu via een limiet bepalen wat de waarde van f(3) moet zijn:
\lim_{x\rightarrow 3}\frac{x^{3}\text{ - }3x^{2}}{x\text{ - }3}=\lim_{x\rightarrow 3}\frac{x^{2}(x\text{ - }3)}{(x\text{ - }3)}=\lim_{x\rightarrow 3}x^{2}=9
De teller kan ontbonden worden in x2(x-3) en zo krijgen we in de teller en de noemer dezelfde factor, namelijk (x-3). En gelijke factoren kunnen worden “weggestreept”. En zo blijft x2 over. En als x=3 dan is x2=9.
We kunnen dus concluderen dat f(3)=9; netter gezegd: Als x naar 3 nadert dan nadert f(x) naar 9.
Er zijn boeken volgeschreven over limieten en het is rauwe kost, maar ik hoop dat deze uitleg voldoende is voor de volgende paragraaf.
Appendix C – Differentiëren
Zoals eerder uitgelegd wil je met differentiëren de raaklijn in een punt van de grafiek bepalen.
Daarvoor wordt de volgende formule gebruikt:
f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)\text{ - }f(x)}{h}
Maar hoe komen we aan deze formule?
Kijk eens naar het volgende figuur:
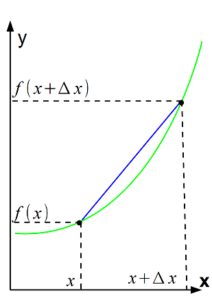
In Figuur 6 is de groene lijn de grafiek van ene f(x). De blauwe lijn is de snijlijn die door de punten f(x) en f(x+Δx) gaat (Δ is de Griekse hoofdletter delta). De formule van een rechte lijn is y = ax + b waarbij a de richtingscoëfficiënt (tegenwoordig ook wel hellingshoek genoemd) is en b het snijpunt met de y-as.
Je kunt deze formule bepalen als je twee punten weet, en in Figuur 6 is dat het geval, namelijk (x, f(x)) en (x+Δx , f(x+Δx)).
Om de richtingscoëfficiënt te bepalen deel je het verschil van de y-waardes van de punten door het verschil van de x-waardes van de punten.
We krijgen dan dus:
\frac{f(x+\Delta x)\text{ - }f(x)}{(x+\Delta x)\text{ - }x}=\frac{f(x+\Delta x)\text{ - }f(x)}{\Delta x}
Maar wat gebeurt er nu als we Δx heel dicht bij x nemen. Zo dicht zelfs dat we op het oog geen verschil meer kunnen zien. Dan wordt de snijlijn een raaklijn. En dan krijgen we de eerste formule, waarbij h de rol van Δx vervult.
Laten we de formule eens gebruiken voor de functie f(x)=x2.
We krijgen dan:
f'(x)=\lim_{h\rightarrow 0}\frac{f(x+h)\text{ - }f(x)}{h}=\lim_{h\rightarrow 0}\frac{(x+h)^{2}\text{ - }x^{2}}{h}=\newline \lim_{h\rightarrow 0}\frac{x^{2}+2xh+h^{2}\text{ - }x^{2}}{h}=\lim_{h\rightarrow 0}\frac{2xh+h^{2}}{h}=\newline \lim_{h\rightarrow 0}2x+h=2x
Dus als f(x) = x2 dan is f’(x) = 2x.
Appendix D – Transcendente getallen
Op de middelbare school heb je, hopelijk, de volgende soorten getallen geleerd:
Natuurlijke getallen – alle positieve gehele getallen (eventueel met 0);
Gehele getallen – alle positieve en negatieve (en 0) gehele getallen;
Rationale getallen – alle getallen die te schrijven zijn als een (niet vereenvoudigbare) breuk a/b met a en b geheel;
Irrationale getallen – alle getallen die niet rationaal zijn, dus niet te schrijven zijn als een breuk a/b met a en b geheel.
Voobeelden:
Natuurlijke getallen: 2, 16, 1024
Gehele getallen: -18, 0, 23
Rationale getallen: -½ , 0, ¾
Irrationale getallen: -√15, √2, e, π
We zien in het laatste voorbeeld dat zowel de wortels als e en π dus irrationale getallen zijn.
Maar toch is er een groot verschil tussen de wortels en e en π.
De wortels zijn oplossingen van polynomiale vergelijkingen. Dat zijn vergelijkingen van de vorm: f(x) = xn + an-1xn-1 + an-2xn-2 + … + a1x + a0.
En zo is √2 een oplossing van de polynoom f(x) = x2 – 2.
Voor iedere wortel is een polynoom te vinden.
Het blijkt echter dat voor e en π er geen polynoom bestaat en deze getallen kennelijk tot een andere categorie behoren.
En in plaats van de getallen onder te verdelen in rationaal en irrationaal kun je ook een ander onderscheid maken.
Oplossingen van polynomen worden algebraïsche getallen genoemd.
Getallen die niet algebraïsch zijn heten transcendente getallen.
De wortels zijn dus voorbeelden van algebraïsche getallen; dit geldt evenzeer voor de rationale, de gehele en de natuurlijke getallen.
De getallen e en π zijn dus transcendent.
De meeste logaritmes zijn (waarschijnlijk) ook transcendent. Het is echter heel lastig om aan te tonen dat een getal transcendent is.
En tot slot een merkwaardig feitje: Er zijn meer transcendente getallen dan algebraïsche getallen (zoals uit de verzamelingenleer van Cantor is gebleken).







