Inhoud
Met de formule van Heron kun je de oppervlakte van een willekeurige driehoek bepalen. De formule van Heron ziet er als volgt uit: a is de zijde tegenover hoek A, b de zijde tegenover hoek B en c is de zijde tegenover hoek C: In dit artikel gaan we deze stelling op een “moderne” manier bewijzen, namelijk met de cosinusregel, die we eerst zullen bewijzen/afleiden. Op het internet zijn diverse sites met hetzelfde bewijs, maar die zijn zeer bondig in de zin dat er veel stappen als vanzelfsprekend worden verondersteld. In dit artikel probeer ik geen enkele stap over te slaan. Omdat we het gaan hebben over de cosinusregel gaan we in deze paragraaf de belangrijkste zaken over goniometrie beknopt behandelen. Voor iedereen die wiskunde in zijn pakket heeft gehad is dit niet meer dan een herhaling. Bekijk onderstaande figuur: We zien een rechthoekige driehoek ABC waarvan we hoek ABC α noemen, hoek CAB β en hoek BCA γ (=90°=½π). We gaan uit van hoek α. De zijde a noemen we de aanliggende (t.o.v. hoek α) rechthoekzijde, zijde b noemen we de overstaande rechthoekzijde (t.o.v. hoek α) en zijde c de schuine zijde of hypotenusa. In deze driehoek zijn nu de volgende verhoudingen gedefinieerd: cos(inus)α = aanliggende rechthoekzijde / schuine zijde = a / c Verder geldt dat: De hoeken worden dan wel in graden gemeten, waarbij een cirkel 360° heeft, dan wel in radialen die betrekking hebben op de omtrek van de cirkel met straal 1, dus 2π. Verder is van belang dat cos(90°)=0 . De cosinusregel luidt als volgt: a2 = b2 + c2 – 2.b.c.cosα. Wanneer je in een driehoek de zijden b en c weet en hoek α, dan kun je met deze regel zijde a bepalen. Er zijn twee varianten op deze regel: b2 = a2 + c2 – 2.a.c.cosβ en Bekijk onderstaande driehoek: In deze driehoek zit ook de rechthoekige driehoek bed verscholen. En in een rechthoekige driehoek kunnen we de stelling van Pythagoras toepassen. I) e2 + d2 = b2 ⇒ d2 = b2 – e2 maar ook: II) (c – e)2 + d2 = a2 ⇒ d2 = a2 – (c – e)2 , Uit I) en II) volgt: En nu zijn we er bijna. De cosinus van een hoek in een rechthoekige driehoek is gedefinieerd als: De aanliggende rechthoekzijde gedeeld door de schuine zijde. In de driehoek hierboven geldt: cosα = e / b en dus e = b.cosα. a2 = b2 + c2 – 2ec = b2 + c2 – 2.b.c.cosα . Merk op dat de cosinusregel een veralgemenisering is van de stelling van Pythagoras. Immers geldt in een rechthoekige driehoek dat α gelijk is aan 90° en de cosinus van 90° is 0, waarmee 2.b.c.cosα gelijk aan nul wordt. En dan hou je dus de stelling van Pythagoras over! De formule van Heron ziet er dus als volgt uit: We pakken de cosinusregel als uitgangspunt en we gaan stap voor stap toewerken naar de formule van Heron waarbij bovenal algebraïsche bewerkingen de hoofdmoot zullen zijn. Laat u hierdoor vooral niet ontmoedigen… We gaan dus uit van: a2 = b2 + c2 – 2.b.c.cosα. De sinα = d / b, dus d = b.sinα. De oppervlakte van een driehoek is ½ × basis × hoogte. In onze driehoek is dat dus: A(ΔABC)= ½ × c × d. Omdat d = b.sinα geldt dus: A(ΔABC) = ½ × c × b.sinα. Met de formule sin2α + cos2α = 1 zien we dat Omdat we hoek α altijd tussen de 0° en 180° kunnen houden geldt dat de sinα altijd groter of gelijk aan 0 is. Daarmee vervalt de – en dus werken we verder met: Dus: Met de cosinusregel kunnen we cosα nu schrijven als: a2 = b2 + c2 – 2.b.c.cosα ⇒ En dus is: cos2α = [(b2 + c2 – a2) / 2b]2. Alles bij elkaar genomen hebben we nu: We gaan moedig verder: We kunnen 1 schrijven als En omdat √(x/y) = √(x)/√(y) krijgen we: Nu is de √(4b2c2) = 2bc. We kunnen nu dus de wortel uit de noemer verwijderen: Het “getal” voor het wortelteken is niets anders dan: Zodat nu overblijft: Houd vol! We zijn al halverwege… We gaan ons nu concentreren op hetgeen er onder het wortelteken staat. We laten dus voor het gemak even het wortelteken weg; op het einde voegen we die weer toe (en de factor ¼ vergeten we ook niet). We kijken dus naar (2bc)2 – (b2 + c2 – a2)2: Merk op dat hier een verschil van 2 kwadraten staat en daar hebben we een merkwaardig product voor. nl.: x2 – y2 = (x – y)(x + y). We krijgen dan: (2bc)2 – (b2 + c2 -a2)2 = (2bc – (b2 + c2 – a2)) (2bc + (b2 + c2 – a2)) Uitgewerkt levert dat op: (2bc – (b2 + c2 – a2)) (2bc + (b2 +c2 – a2)) = (2bc – b2 – c2 + a2) (2bc + b2 + c2 – a2) We gaan nu de a2 er buiten halen en wat husselen met de volgorde: ((-b2 + 2bc – c2) + a2) ((b2 + 2bc + c2) – a2) Om de – bij de b2 en c2 weg te halen schrijf ik ((-b2 + 2bc – c2) + a2) nu als: (a2 – (b2 – 2bc + c2)). Dan wordt de laatste expressie: (a2 – (b2 – 2bc + c2)) ((b2 + 2bc + c2) – a2) In de binnenste haken zien we respectievelijk de merkwaardige producten (x – y)2 = x2 – 2xy + y2 en (x + y)2 = x2 + 2xy + y2, We krijgen dus: a2 – (b – c)2) (b + c)2 – a2 En nu kunnen we 2 keer het merkwaardige product x2 – y2 = (x – y)(x + y) zien. Dus krijgen we: (a – (b – c)) (a + (b – c)) ((b + c) – a) ((b + c) + a) en dat is te schrijven als (haakjes wegwerken): (a – b + c) (a + b – c) (b + c – a) (a + b + c). Nu gaan we de halve omtrek erin verwerken: De halve omtrek: s = (a + b + c) / 2 ⇒ (a – b + c) (a + b – c) (b + c – a) (a + b + c) = Tijd om onze ¼ en wortel terug te halen: De 16 onder de wortel vandaan halen: En als we nu tot slot de volgorde van de factoren veranderen dan hebben we eindelijk de formule van Heron: Ik geef toe dat het een heel karwij was maar we hebben iedere mogelijke stap uitgewerkt, en dat was het doel van dit artikel. Inleiding
De formule die je waarschijnlijk op school hebt geleerd luidt: De oppervlakte van een driehoek is gelijk aan de halve basis keer de hoogte. In formulevorm: A(Δabc)=½basis×hoogte. Maar het is vaak moeilijk om de hoogte op een basis te bepalen. Met de formule van Heron heb je hier geen last van.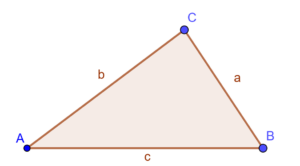
Goniometrie
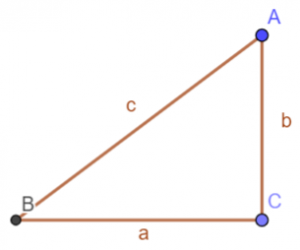
sin(us)α = overstaande rechthoekzijde / schuine zijde = b / c
tan(gens)α = overstaande rechthoekzijde / aanliggende rechthoekzijde = b / a = sinα / cosα.
sin2α + cos2α = 1 .De cosinusregel
c2 = a2 + b2 – 2.a.b.cosγ.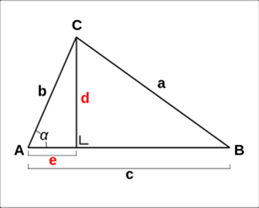
Nu is (c – e)2 een merkwaardig product dat we kunnen uitwerken:
(c – e)2 = c2 – 2ec + e2 en dus:
d2 = a2 – [c2 – 2ec + e2] = a2 – c2 + 2ec – e2
b2 – e2 = a2 – c2 + 2ec – e2 ⇒
b2 = a2 – c2 + 2ec ⇒
b2 – a2 = -c2 + 2ec ⇒
-a2 = -b2 – c2 + 2ec ⇒
a2 = b2 + c2 – 2ec .
Substitueren we dit in de laatste formule dan krijgen we:De formule van Heron
sin2α = 1 – cos2α en dus dat
sinα = ±√(1 – cos2α).
sinα = √(1 – cos2α)
A(ΔABC) = ½ × c × b.sinα = ½ × c × b × √(1 – cos2α).
a2 – b2 – c2 = -2.b.c.cosα ⇒
2.b.c.cosα = b2 + c2 – a2 ⇒
cosα = (b2 + c2 – a2) / 2b .
1 = (4b2c2) / (4b2c2), daarmee krijgen we dan:
a + b + c = 2s ⇒
a + b = 2s – c en
a + c = 2s – b en
b + c = 2s – a .
(a + c – b) (a + b – c) (b + c – a) (a + b + c) =
(2s – b – b) (2s – c – c) (2s – a – a) 2s =
(2s – 2b) (2s – 2c) (2s – 2a) 2s =
2(s – b) 2(s – c)2 (s – a) 2s =
2.2.2.2(s – b) (s – c) (s – a) s =
16(s – b) (s – c)(s – a) s .
Formule van Heron
A(\Delta ABC)=\sqrt{s(s-a)(s-b)(s-c)} \\ \small \text{, met s = }\frac{1}{2}(a+b+c)
A(\Delta ABC)=\sqrt{s(s-a)(s-b)(s-c)} \\ \small \text{, met s = }\frac{1}{2}(a+b+c)
A(\Delta ABC)=\frac{1}{2}bc\sqrt{1-cos^{2}\alpha}= \\ \frac{1}{2}bc\sqrt{1-\left( \frac{b^{2}+c^{2}-a^{2}}{2bc} \right)^{2}}= \\ \frac{1}{2}bc\sqrt{1-\frac{\left( b^{2}+c^{2}-a^{2} \right)^{2}}{4b^{2}c^{2}}}
A(\Delta ABC)=\frac{1}{2}bc\sqrt{\frac{4b^{2}c^{2}-\left( b^{2}+c^{2}-a^{2} \right)^{2}}{4b^{2}c^{2}}}
A(\Delta ABC)=\frac{1}{2}bc{\frac{\sqrt{4b^{2}c^{2}-\left( b^{2}+c^{2}-a^{2} \right)^{2}}}{\sqrt{4b^{2}c^{2}}}}
A(\Delta ABC)=\frac{1}{2}bc\frac{1}{2bc}{\sqrt{4b^{2}c^{2}-\left( b^{2}+c^{2}-a^{2} \right)^{2}}}
\frac{1}{2}bc.\frac{1}{2bc}=\frac{1. \cancel{bc}}{2.2 \cancel{bc}}=\frac{1}{2.2}=\frac{1}{4}
A(\Delta ABC)=\frac{1}{4}{\sqrt{(2bc)^{2}-\left( b^{2}+c^{2}-a^{2} \right)^{2}}}
A(\Delta ABC)=\frac{1}{4}\sqrt{16(s-b)(s-c)(s-a)s}
A(\Delta ABC)=\frac{1}{4}.\sqrt{16}\sqrt{(s-b)(s-c)(s-a)s}= \\ \frac{1}{4}.4\sqrt{(s-b)(s-c)(s-a)s}= \\ \sqrt{(s-b)(s-c)(s-a)s}
A(\Delta ABC)=\sqrt{s(s-a)(s-b)(s-c)} \\ \small \text{, met }s=\frac{1}{2}(a+b+c)