Inleiding
In deze aflevering zal ik op eenvoudige wijze proberen een aantal veel gebruikte statistische termen uit te leggen. Ik zal dat zowel technisch doen alsook de betekenis erbij geven. Er is echter een bekend gezegde, dat de geachte lezer altijd in gedachte moet houden wanneer hij of zij met statistiek bezig is.
Er zijn drie soorten leugens: 1. Een leugentje om bestwil, 2. Een grove leugen en 3. Statistiek.
Waarnemingsgetallen
Waarnemingsgetallen zijn niets anders dan de resultaten van een of andere test of onderzoek. Te denken valt hierbij aan de cijfers van een klas, temperaturen in de wintertijd, aantal gereden kilometers per dag gedurende een jaar, etcetera.
Modus
De modus is het waarnemingsgetal dat het meeste voorkomt in een verzameling waarnemingsgetallen. Kijk maar naar de volgende verzameling: {1, 2, 3, 3, 3, 4, 5, 5, 6, 7}. Het getal 3 komt het meeste voor en is daarom de modus. Wanneer er meer getallen even vaak (en het meest) voorkomen, dan is er geen modus.
Mediaan
De mediaan is het middelste waarnemingsgetal van een verzameling gesorteerde waarnemingsgetallen. Wanneer de verzameling een even aantal elementen bevat, dan is de mediaan het gemiddelde van de twee middelste waarnemingsgetallen. In de verzameling {1, 2, 3, 3, 4, 5, 5, 6, 7} is 4 de mediaan, in de verzameling {1, 2, 3, 3, 3, 4, 5, 5, 6, 7} is de mediaan het gemiddelde van 3 en 4, en dat is 3½.
Gemiddelde
Het gemiddelde van een verzameling waarnemingsgetallen is het quotiënt van de som der waarnemingsgetallen en het aantal waarnemingsgetallen. We praten hier overigens over een “rekenkundig” gemiddelde. Iedereen heeft wel een intuïtief gevoel van het begrip gemiddelde, maar statistisch gezien heb je er vrij weinig aan.
Het gemiddelde van de waarnemingsgetallen {1, 2, 3, 3, 3, 4, 5, 5, 6, 7} is dus 1+2+3+3+3+4+5+5+6+7=39 gedeeld door 10 (het aantal waarnemingsgetallen) is 3,9.
Een relevantere vraag is of bv. 3 ook “gemiddeld” is. En wat te denken van 7?
Standaarddeviatie
Deviatie is een ander woord voor afwijking. We praten hier over een afwijking van een waarnemingsgetal ten opzichte van het gemiddelde. We kunnen dit per waarnemingsgetal bepalen, maar we willen eigenlijk 1 “maat” van afwijking voor de gehele verzameling waarnemingsgetallen hebben. Dat laatste noemen we de standaarddeviatie of standaardafwijking. Technisch gezien is de standaarddeviatie de wortel van het quotiënt van de som der afwijkingen in het kwadraat en het aantal waarnemingsgetallen. Dat is natuurlijk een prachtige volzin, maar laten we het toch maar even illustreren.
Kijken we naar de volgende verzameling waarnemingsgetallen: {1, 3, 4, 5, 7}.
| waarnemingsgetal | afwijking tov gem. | afw2 | |
| 1 | 1-4=-3 | -32=9 | |
| 3 | 3-4=-1 | -12=1 | |
| 4 | 4-4=0 | 02=0 | |
| 5 | 5-4=1 | 12=1 | |
| 7 | 7-4=3 | 32=9 | |
| som | 20 | som | 20 |
| aantal | 5 | aantal | 5 |
| gemiddelde | 20/5=4 | standaarddeviatie | √(20/5)=√4=2 |
Allereerst bepalen we het gemiddelde. In dit voorbeeld is dat 4. Dan gaan we van ieder afzonderlijk waarnemingsgetal de afwijking t.o.v. het gemiddelde bepalen. Deze vind je in de derde kolom. Dan bepaal je per afwijking het kwadraat, zie vierde kolom. Dan bepaal je de som van alle afwijkingen in het kwadraat en deel je die door het aantal waarnemingsgetallen. Tot slot trek ja van het verkregen getal de wortel, en je hebt de standaarddeviatie van de gehele verzameling.
Wat zegt de standaarddeviatie ons nu? In de vorige paragraaf stelden we de vraag of bepaalde waarnemingsgetallen nu “gemiddeld” waren of niet. Met de standaarddeviatie in handen kunnen we deze vragen beantwoorden, waarbij we de volgende vuistregel hanteren. Ieder waarnemingsgetal dat binnen twee keer de standaarddeviatie van het gemiddelde ligt is niet uitzonderlijk.
In ons voorbeeld zijn dus alle getallen tussen 0 (=4-2×2) en 8 (=4+2×2) niet uitzonderlijk. Dat geldt in dit voorbeeld voor alle getallen!
Wanneer je dus een of ander statistisch onderzoek leest, dan zegt het gemiddelde alleen maar iets wanneer ook de standaarddeviatie is gegeven. Een leerling die een 10 haalt met een gemiddelde van 5 hoeft dus niet uitzonderlijk te zijn.
Correlatie ofwel appels en peren
Een vaak gehoorde uitdrukking is dat je appels en peren niet met elkaar kunt vergelijken. In de statistiek kan dit echter wel!
Door middel van correlatie kun je twee verzamelingen met waarnemingsgetallen met elkaar in verband brengen. Ik ga hier niet een exacte definitie of formule van correlatie geven, want dat is te ingewikkeld. De methode om tot een correlatiecoëfficiënt (zo heet dat nu eenmaal officieel) te komen is echter niet zo ingewikkeld. Allereerst moeten we de waarnemingsgetallen uit de twee verzamelingen “normaliseren”. Dat betekent dat we aan alle waarnemingsgetallen een nieuwe waarde moeten toekennen zodat ze wel met elkaar vergeleken kunnen worden. Om van een waarnemingsgetal tot een normaalgetal te komen delen we de afwijking van dat waarnemingsgetal door de standaarddeviatie. Voor de verzameling van waarnemingsgetallen uit de vorige paragraaf komen we dan tot de volgende tabel:
| waarnemingsgetal | afwijking tov gem. | normaalgetal | |
| 1 | 1-4=-3 | -3/2=-1,5 | |
| 3 | 3-4=-1 | -1/2=-0,5 | |
| 4 | 4-4=0 | 0/2=0 | |
| 5 | 5-4=1 | ½=0,5 | |
| 7 | 7-4=3 | 3/2=1,5 | |
| som | 20 | ||
| aantal | 5 | ||
| gemiddelde | 20/5=4 | standaarddeviatie | 2 |
Nu zou het handig zijn als we een tweede verzameling waarnemingsgetallen hadden. Vooruit dan maar: {50, 90, 70, 10, 130}. Dit levert de volgende tabel op:
| waarnemingsgetal | afwijking tov gem. | normaalgetal | |
| 50 | 50-70=-20 | -20/40=-0,5 | |
| 90 | 90-70=20 | 20/40=0,5 | |
| 70 | 70-70=0 | 0/40=0 | |
| 10 | 10-70=-60 | -60/40=-1,5 | |
| 130 | 130-70=60 | 60/40=1,5 | |
| som | 350 | ||
| aantal | 5 | ||
| gemiddelde | 350/5=70 | standaarddeviatie | 40 |
Als het goed is moeten je nu twee dingen opvallen: 1. de grootte van de waarnemingsgetallen van de twee verzamelingen liggen nogal uiteen, terwijl 2. de normaalgetallen, qua grootte, dicht bij elkaar liggen.
De correlatiecoëfficiënt verkrijgen we nu als volgt: 1. Vermenigvuldig de normaalgetallen paarsgewijs met elkaar, 2. Bepaal vervolgens hun som en 3. Deel de som door het aantal paren normaalgetallen. Kijk naar het resultaat maar naar de volgende tabel:
| normaalgetal 1 (n1) | normaalgetal 2 (n2) | n1xn2 |
| -1,5 | -0,5 | 0,75 |
| -0,5 | 0,5 | -0,25 |
| 0 | 0 | 0 |
| 0,5 | -1,5 | -0,75 |
| 1,5 | 1,5 | 2,25 |
| som | 2 | |
| aantal | 5 | |
| correlatiecoëf. | 2/5=0,4 |
Wat zegt ons die 0,4 nu eigenlijk?
Een correlatiecoëfficiënt ligt altijd tussen de –1 en de 1. In het algemeen kunnen we zeggen dat twee verzamelingen correlatie vertonen als de correlatiecoëfficiënt kleiner is dan –0,5 of groter is dan 0,5. Hoe meer de correlatiecoëfficiënt naar de –1 of de 1 kruipt, hoe meer verband er is tussen de twee verzamelingen waarnemingsgetallen.
In ons voorbeeld is er dus eigenlijk geen overtuigend verband tussen de twee verzamelingen.
Tot slot nog een paar opmerkingen:
- Om de correlatiecoëfficiënt te kunnen bepalen is de volgorde van de waarnemingsgetallen in de verzameling belangrijk.
- Het aantal waarnemingsgetallen in beide verzamelingen moet gelijk zijn.
- Wanneer de correlatiecoëfficiënt positief is wil dat zeggen dat wanneer de elementen van de ene verzameling groter worden, dat in de andere verzameling ook zal gebeuren.
- Wanneer de correlatiecoëfficiënt negatief is wil dat zeggen dat wanneer de elementen van de ene verzameling groter worden, de elementen in de andere verzameling juist kleiner worden.
Correlatie 2
Er is nog een andere manier om de correlatiecoëfficiënt uit te rekenen. Bepaal het quotiënt van de covariantie en het product van de standaarddeviatie en je krijgt de correlatiecoëfficiënt.
De covariantie van twee verzamelingen waarnemingsgetallen is ook een maat voor afhankelijkheid tussen beide verzamelingen. Daar echter de covariantie niet “genormaliseerd” is, is het in de praktijk niet handig om dat daarvoor te gebruiken.
Het is echter niet moeilijk om de covariantie van twee verzamelingen waarnemingsgetallen te bepalen. Dat gaat als volgt: Bepaal het gemiddelde van de som van de producten van de paarsgewijze waarnemingsgetallen. Bepaal dan het product van de gemiddelden van de verzamelingen waarnemingsgetallen en trek de laatste nu van de eerste af. Dat getal is de covariantie. Kijk maar weer naar onderstaande tabel:
| waarnemingsgetal 1 (w1) | waarnemingsgetal 2 (w2) | w1*w2 | |
| 1 | 50 | 50 | |
| 3 | 90 | 270 | |
| 4 | 70 | 280 | |
| 5 | 10 | 50 | |
| 7 | 130 | 910 | |
| som | 20 | 350 | 1560 |
| aantal | 5 | 5 | 5 |
| gemiddelde | 4 | 70 | 1560/5=312 |
| standaarddeviatie | 2 | 40 | |
| gem1*gem2 | 280 | ||
| covariantie | 312-280=32 | ||
| sd1*sd2 | 80 | ||
| correlatiecoëf. | 32/80=0,4 |
In de laatste twee regels van de tabel worden achtereenvolgens het product van de standaarddeviaties van de twee verzamelingen waarnemingsgetallen en de correlatiecoëfficiënt bepaald.
Regressie
Door middel van regressie kunnen we bepalen door welke (rechte) lijn de grafiek van de twee verzamelingen waarnemingsgetallen het best wordt bepaald. Ik bedoel natuurlijk dat je de twee verzamelingen waarnemingsgetallen tegen elkaar uitzet.
Wanneer we beide verzamelingen uit de vorige paragrafen tegen elkaar uitzetten krijgen we de volgende grafiek:
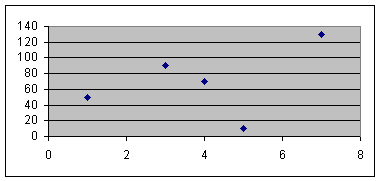
Kunnen we nu een rechte lijn bedenken die deze grafiek het best benadert? Het antwoord is natuurlijk ja, want anders was ik niet aan deze paragraaf begonnen.
Even een opmerking tussendoor: Omdat de correlatiecoëfficiënt in ons voorbeeld vrij laag is, zal de lijn die we gaan zoeken natuurlijk niet al te best zijn.
Een rechte lijn heeft de volgende algemene formule: y=ax+b, waarbij a de zgn. richtingscoëfficiënt is en b het snijpunt met de y-as is. Vanuit onze voorgaande statistische analyses kunnen we a en b gemakkelijk bepalen. Namelijk: a=r*(sd2/sd1), waarbij r de correlatiecoëfficiënt is en sd1 en sd2 resp. de standaarddeviatie van de eerste en de tweede verzameling waarnemingsgetallen is, en b=g2-a*g1, waarbij g1 en g2 resp. het gemiddelde van de eerste en tweede verzameling waarnemingsgetallen is.
In onderstaande tabel bepalen we a en b:
| g1 | 4 |
| sd1 | 2 |
| g2 | 70 |
| sd2 | 40 |
| r | 0,4 |
| a=r*(sd2/sd1) | 0,4*(40/2)=8 |
| b=g2-a*g1 | 70-8*4=38 |
| y=ax+b | y=8x+38 |
De lijn y=8x+38 is de beste benadering voor vervanging van onze grafiek. Getekend in de grafiek komt e.e.a. er als volgt uit te zien:
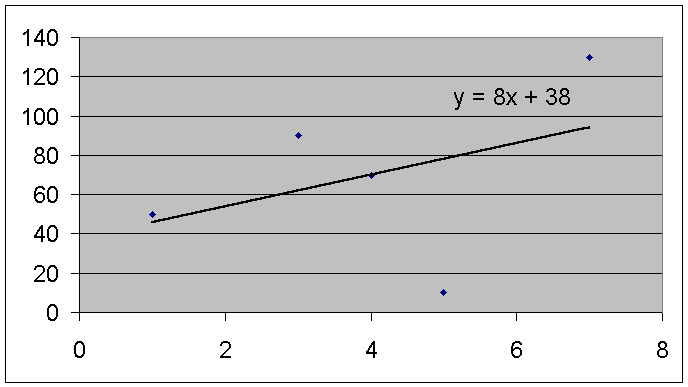
Ook kunnen we door de formule voorspellen wat de overeenkomstige waarde in de tweede verzameling waarnemingsgetallen zal zijn voor een niet bestaand waarnemingsgetal in de eerste verzameling waarnemingsgetallen.
Hoe hoger echter de correlatiecoëfficiënt, hoe beter zo’n voorspelling natuurlijk zal zijn.
Ter afsluiting
In deze aflevering heb ik hopelijk laten zien dat statistiek, althans een klein maar veel gebruikt gedeelte daarvan, eigenlijk helemaal niet zo moeilijk is als sommige instanties ons willen doen geloven. Het was echter ook een redelijk technisch verhaal. De lezer dient zich te realiseren dat conclusies trekken uit statistische feiten erg gevaarlijk kan zijn. Er zijn best statistische methodes om waardes te geven aan eventuele foutmarges, maar het blijft toch een riskante zaak.
Ik realiseer me goed, dat ik aan een aantal zaken voorbij ben gegaan. Belangrijke zaken als bijvoorbeeld normaalverdelingen en dergelijke. Maar het was dan ook niet mijn bedoeling om de statistiek hier uitputtend te behandelen.
Wel hoop ik bereikt te hebben dat de lezer in het vervolg kritischer naar statistische publicaties zal kijken, en zich bijvoorbeeld realiseren dat het melden van een gemiddelde zonder het melden van de standaarddeviatie daarbij, redelijk nutteloos is.