Inhoud
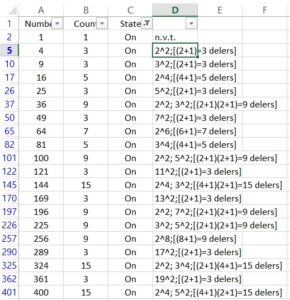
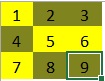
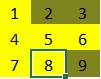
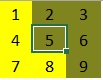
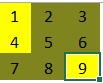
In deze aflevering gaan we kijken naar het zogenaamde “Schakelaar probleem”. Er is een vierkant bord met n × n aan/uit-schakelaars met een lampje erboven. Kunt u van te voren bedenken welke lampjes aan staan en welke uit nadat iedere persoon aan de beurt is geweest? Met het Excel programma LightSwitchProblem (zip-bestand) kunt u zelf experimenteren. Uitleg programma Allereerst moet u er voor zorgen dat Excel macro’s accepteert (zie VBA voor programmeurs). Er zijn 3 tabbladen: Play, Stats en Explanation. Het programma start met het tabblad Explanation. Hierop kunt u aangeven uit hoeveel schakelaars het bord bestaat, hoeveel tijd in ms elke klik op een schakelaar duurt en of er na iedere speler gewacht moet worden (druk dan op Enter voor de volgende speler) zodat u het bord na iedere beurt kunt inspecteren. Het tabblad Play wordt geactiveerd en u ziet het bord met de schakelaars (lampjes). Een bruin vakje betekent “uit” en een geel vakje betekent “aan”. Nadat het spel gespeeld is kunt u op het tabblad Stats wat statistieken zien. Het programma is “open-source” wat betekent dat u de code gewoon mag inzien en naar eigen believen mag aanpassen. Laten we eens kijken naar een bord met 9 schakelaars (3 × 3). Bij aanvang ziet het bord er als volgt uit: Alle schakelaars (lampjes) staan uit. Speler 1 begint nu op schakelaar 1 te drukken en vervolgens op alle veelvouden van 1; kortom: Speler 1 drukt op alle schakelaars en alle lampjes zullen dus gaan branden: Nu is Speler 2 aan de beurt: Deze begint op schakelaar 2 en zal op alle even schakelaars drukken; deze zullen hierna dus uit staan: Tot zover is het allemaal redelijk voorstelbaar. Nu komt Speler 3 aan de beurt die dus begint op schakelaar 3 en daarna op schakelaar 6 en 9 drukt: En nu begint het er al wat onvoorspelbaarder uit te zien. Na Speler 4: Na Speler 5: Merk op dat vanaf Speler 5 de Spelers alleen nog maar op de schakelaar met hun eigen nummer drukken. Nadat iedereen gedrukt heeft ziet het bord er als volgt uit: De schakelaars met nummers 1, 4 en 9 zijn aan, de rest is uit. Wanneer u zelf de Excel simulatie heeft dan kunt u na de simulatie een kijkje nemen op het tabblad Stats: In de kolom Number staat het nummer van de schakelaar. We zien hierboven dat de schakelaars 1, 4 en 9 aan staan. Laten we eens gaan filteren op State=On: En op State=Off: Kijken we bij bovenstaande 2 afbeeldingen naar de kolom Count dan valt wellicht op dat het getal Count bij State=On een oneven getal is, en bij State=Off een even getal. Wanneer u met grotere borden werkt en daarna op het tabblad Stats kijkt dan zult u zien dat dat geen toeval is. Het blijkt dat wanneer een schakelaar aan staat deze een oneven aantal keer is omgezet. Staat de schakelaar uit dat dat is de schakelaar een even aantal keer omgezet. Maar op welke schakelaars worden nu een even aantal keer gedrukt en op welke een oneven aantal? Laten we nog eens kijken naar de gefilterde tabel (State=On) bij een 20 x 20 bord: Wat voor soort getallen staan er nu eigenlijk in de kolom Number? Maar waarom worden schakelaars met een geheel kwadraat als nummer een oneven aantal keer omgezet? Dit heeft alles te maken met de priemontbinding van een getal. In ons decimaal stelsel is ieder getal op unieke wijze te ontbinden in priemfactoren (zie ook Hoofdstelling van de rekenkunde). Zo is 12 = 2 × 6, maar 6 = 2 × 3, dus 12 = 2 × 2 × 3. En de exponenten van de priemfactoren zijn een maat voor het aantal delers van een getal. Het aantal delers van een getal is namelijk het product van alle exponenten plus 1 van de priemfactoren. Zo heeft 12 dus (2 + 1)(1 + 1) = 3 × 2 = 6 delers. De priemontbinding van 6 = 21 × 31. De conclusie is gerechtvaardigd dat het aantal keer dat een schakelaar met een bepaald nummer wordt bezocht gelijk is aan het aantal delers van het nummer van die schakelaar. Maar blijft de vraag open waarom een geheel kwadraat een oneven aantal delers heeft en een samengesteld getal een even aantal delers heeft. Welnu: De delers van een samengesteld getal komen altijd in paren voor. Kijk maar: Laten we als voorbeeld maar weer even 12 nemen: Wanneer je weet dat 1 een deler is van 12 dan ook 12 zelf, Zie daar de delers van 12: (1 en 12), (2 en 6) en (3 en 4): 3 paartjes delers. Je vindt alle paartjes door te kijken naar de getallen kleiner dan de wortel van een getal, daarna heb je ze allemaal gevonden. En die wortel is precies het antwoord waarom een geheel kwadraat een oneven aantal delers heeft. Kijk maar eens naar 36. De paartjes zijn: (1 en 36), (2 en 18), (3 en 12), (4 en 9) en (6 en 6). Maar dat laatste paartje levert maar 1 deler op, en dat is precies de wortel van 36. Maar hoe dan ook, 36 heeft een oneven aantal delers. En dat geldt dus voor ieder geheel kwadraat omdat de wortel van een geheel kwadraat een geheel getal is. Dat betekent voor onze schakelaars dat de schakelaars met een geheel kwadraat als nummer een oneven aantal keren zullen worden ingedrukt. Extra functie in Excel simulatie In de Excel simulatie kunt u in het tabblad Stats gebruik maken van de UDF (User Defiened Function) GivePrimes(<Number>). Deze functie geeft de priemontbinding van <Number> met daarbij het aantal delers van <Number>. Dus in cel D5 staat de formule: =GivePrimes(A5).Inleiding
We kijken naar voorbeelden en we maken een analyse.
Tevens kunt u zelf, met behulp van een simulatie in Excel, ook hiermee spelen en kijken of u zelf van te voren kunt bedenken wat de uitkomsten zijn.Het probleem
Bij aanvang staan alle schakelaars op de uit-stand en zijn alle lampjes gedoofd.
Er zijn ook n2 mensen genummerd vanaf 1 tot en met n2.
Persoon 1 begint, daarna 2 etc.
Persoon n drukt op schakelaar n en op alle schakelaars die een veelvoud zijn van n.
Als een schakelaar uit staat en er wordt op gedrukt dan gaat de schakelaar, met het lampje daarboven, aan en vice versa.Simulatie
Op dat tabblad staat een knop Play.
Wanneer u daarop klikt krijgt u een invulscherm:
Daarna klikt u op de knop Play van het invulscherm.
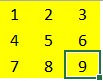
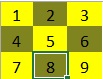
Analyse
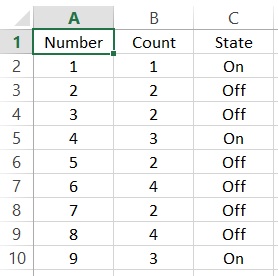
In de kolom Count staat hoe vaak de schakelaar is omgezet.
In de kolom State staat de uiteindelijke stand van de schakelaar.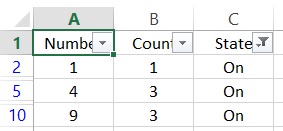
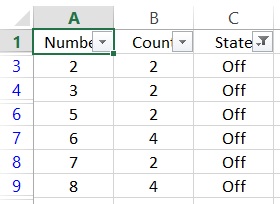
Uiteraard is dat logisch!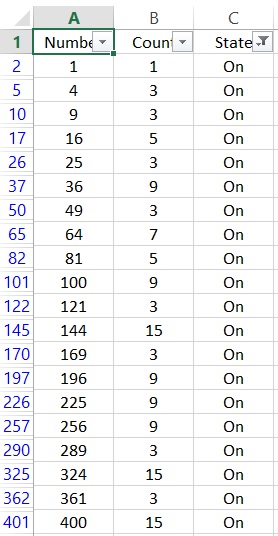
Dat zijn allemaal gehele kwadraten!Verklaring
Maar 12 = 3 × 4, maar 4 = 2 × 2, dus 12 = 3 × 2 × 2.
Beide ontbindingen leiden tot dezelfde priemfactorisatie: 2 × 2 × 3 ofwel 22 × 31.
En dat klopt want de delers van 12 zijn: 1, 2, 3, 4, 6 en 12.
Het aantal delers van 6 is dus (1 + 1)(1 + 1) = 2 × 2 = 4.
En in één van de tabellen hierboven kunt u zien dat het aantal keer dat schakelaar 6 is bezocht precies 4 keer is.
En als je weet dat 2 een deler is van 12 dan ook 6,
En als je weet dat 3 een deler is van 12 dan ook 4.
Je zou ook kunnen zeggen dat 6 “samen valt met” 6.
En omdat alle schakelaars uit staan bij het begin zullen de schakelaars met een geheel kwadraat als nummer bij het einde dus aan staan.