Inhoud
De stelling van Wilson zegt dat als p een priemgetal is dan is p een deler van (p – 1)! + 1. Een opmerkelijke eigenschap van priemgetallen. Waarom het de stelling van Wilson heet is mij niet bekend. Wilson was een 18e-eeuwse wiskundige maar de stelling dateert al zeker vanaf de 10e eeuw. Wilson zelf was niet in staat deze stelling te bewijzen. Een eerste bewijs dook op in 1771 door de wiskundige Lagrange. Laten we eens naar een voorbeeld kijken: We nemen het priemgetal 11. De stelling zegt nu dat 11 een deler is van 10! + 1. rbz, rzb, brz, bzr, zrb en zbr. Dus op totaal 6 verschillende manieren en dat is precies 3! = 1 × 2 × 3. Terug naar ons voorbeeld 11. 10! + 1 = 3.628.801, en 3.628.801 ÷ 11 = 329.891. Probeer zelf maar eens met andere priemgetallen. Neem ze echter niet te groot want een faculteit loopt al vlug uit de klauwen… De wiskundige manier om de stelling van Wilson neer te schrijven is: Als p is priem, dan p | (p – 1)! + 1. Een andere manier om deze stelling te noteren is de volgende: (p – 1)! + 1 ≡ 0 (mod p) of (p – 1)! ≡ -1 (mod p). De ≡ staat voor “congruent”. De mod staat voor “modulo”. En dit laatste heeft alles te maken met klokrekenen. Klokrekenen heeft alles te maken met delen met resten. Ofwel de ouderwetse staartdeling komt hierbij goed van pas. We noemen het klokrekenen omdat de analoge klok met wijzers een bekend gegeven is. Laten we eens kijken naar de 12-urige klok. Stel het is 9 uur: Hoe laat is het dan over 5 uur (op de 12-urige klok)? Het is dan dus 2 uur. Maar hoe berekenen we dit nu? Steeds als de 12 wordt gepasseerd trekken we er 12 vanaf, zodat we altijd in de range 1 t/m 12 blijven. Wiskundig schrijven we nu: 9 + 5 ≡ 2 (mod 12) (Spreek uit: “negen plus vijf is congruent met 2 modulo twaalf“). Nog wat voorbeelden zonder klok: 6 + 5 ≡ 4 (mod 7), ofwel als je 6 optelt bij 5 krijg je 11 en als je 11 door 7 deelt hou je 4 over. Maar wat heeft dit nu allemaal te maken met de stelling van Wilson? In het laatste voorbeeld uit de vorige paragraaf hebben we gezien dat wanneer een deling “uit komt”, dus de deler past precies een geheel aantal keer in het deelgetal, de rest nul is. Laten we nog eens kijken naar het priemgetal 11. De stelling zegt dus dat 11 geheel past in (11 – 1)! + 1 ofwel dat (10! + 1) ÷ 11 = 0 We gaan dit eens uitschrijven: 10! + 1 = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 + 1. We gaan nu deze vermenigvuldiging berekenen modulo 11. Daarvoor gaan we kijken naar de rest-tabel van delen-door-11. De mogelijke resten die bij deling door 11 kunnen optreden zijn de getallen 1 tot en met 10. Uit de tabel kun je bijvoorbeeld lezen dat als ik 3 met 8 vermenigvuldig er een rest van 2 over blijft. De interessante uitkomsten in de tabel zijn die met een rest van 1. Dat geldt bijvoorbeeld voor 3 en 4, dus 3 × 4 geeft een rest van 1. Maar dat betekent dus dat we: 10! + 1 = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 + 1 (mod 11) nu kunnen schrijven als: 10! + 1 = 1 × 2 × 1 × 5 × 6 × 7 × 8 × 9 × 10 + 1 (mod 11). Ook 2 × 6 levert een rest van 1 op, dus: 10! + 1 = 1 × 2 × 1 × 5 × 6 × 7 × 8 × 9 × 10 + 1 (mod 11) kunnen we schrijven als: 10! + 1 = 1 × 1 × 1 × 5 × 7 × 8 × 9 × 10 + 1 (mod 11). En 5 × 9 geeft een rest van 1, dus: 10! + 1 = 1 × 1 × 1 × 5 × 7 × 8 × 9 × 10 + 1 (mod 11) geeft: 10! + 1 = 1 × 1 × 1 × 1 × 7 × 8 × 10 + 1 (mod 11). En ook 7 × 8 heeft 1 als rest, dus 10! + 1 = 1 × 1 × 1 × 1 × 7 × 8 × 10 + 1 (mod 11) geeft: 10! + 1 = 1 × 1 × 1 × 1 × 1 × 10 + 1 (mod 11). En wat we nu over hebben is: 10! + 1 = 1 × 1 × 1 × 1 × 1 × 10 + 1 = 1 × 10 + 1 = 11 = 0 (mod 11). En uiteraard is 11 deelbaar door 11, niet waar? Waar het hier op neer komt is dat we alle factoren paarsgewijs kunnen vervangen door 1, behalve 1 en 11, waardoor we de uitgebreide vermenigvuldiging kunnen reduceren tot 10 (11 – 1). We gaan verderop in deze aflevering het hier bovenstaande formaliseren, zodat we een net bewijs voor de stelling kunnen leveren. Tot slot van deze paragraaf gaan we eens kijken of en eventueel waar bovenstaande methode misgaat bij een samengesteld getal. Laten we hiervoor het getal 10 nemen. We gaan dus kijken naar: 9! + 1 = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 + 1 (mod 10). Laten we de rest-tabel van delen-door-10 er eens bijhalen: We zien hier dat 4 × 5 een rest van 0 oplevert, dus 9! + 1 = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 + 1 (mod 10) kunnen we schrijven als: 9! + 1 = 1 × 2 × 3 × 0 × 6 × 7 × 8 × 9 + 1 (mod 10). Maar als één van de factoren van een vermenigvuldiging 0 is dat is de hele vermenigvuldiging dus 0. We houden nu dus over: 9! + 1 = 1 (mod 10). En als we 1 delen door 10 houden we een rest van 1 over en dus is 10 geen deler van (10 – 1)! + 1. De methode gaat mis omdat er in de rest-tabel nullen staan. Maar voordat we overgaan naar een formeel bewijs moeten we eerst iets weten of groepen. In de wiskunde is een groep een (niet lege) verzameling (getallen) die onder een bepaalde bewerking aan een 4-tal eisen moeten voldoen. De notatie van een groep is: (G, *), waarbij G de verzameling is en * de bewerking. Omdat * tegenwoordig wordt gebruikt voor vermenigvuldiging gebruiken we hier een iets andere notatie voor een groep: (G, #), waarbij # dus de bewerking is. Zo kan # dus bijvoorbeeld een optelling of vermenigvuldiging zijn. De 4 eisen van een groep zijn: Het kan ook nog zijn dat een groep onder de bewerking commutatief is. Dat wil zeggen dat voor iedere a, b ∈ G geldt dat a # b = b # a (∈ G). Dan spreken we van een Abelse groep (vernoemd naar de wiskundige Niels Abel). Wat voorbeelden: De verzameling der gehele getallen (ℤ) onder de optelling is een groep: (ℤ, +). Laten we dit eens bekijken: Verder geldt ook dat voor iedere a, b ∈ ℤ dat a + b = b + a (commutatief) dus is (ℤ, +) zelfs een Abelse groep. (ℤ, -), (ℚ\{0}, ×), ({1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, × (mod 11)) zijn ook allemaal groepen. Geen groep is bijvoorbeeld: (ℕ, +), want het ontbreekt hier aan een inverse element. En hier volgt dan het bewijs: Aanname (dus zonder bewijs): Voor ieder priemgetal p > 2 is de verzameling G = {1, 2, 3, 4, …, p-1} onder de vermenigvuldiging modulo p een groep, dus (G, × (mod p)). Dit betekent dat (bijna) iedere a ∈ G een inverse a-1 ∈ G heeft zodat a × a-1 ≡ 1 (mod p), waarbij 1 het eenheidselement van (G, mod p) is. Dus (bijna) ieder element van G heeft een inverse (ongelijk aan zichzelf). Dit betekent dat als alle elementen met hun inverse paarsgewijs bij elkaar worden genomen en met elkaar worden vermenigvuldigd het product (p – 1)! + 1 ≡ 0 (mod p). Hierboven staat twee keer (bijna) want alle elementen hebben een verschillende inverse behalve 1 en p – 1. Het bewijs hierboven geldt voor ieder priemgetal groter dan 2. Maar 2 is zelf ook een priemgetal. Geldt de stelling van Wilson ook voor 2? Welnu: Is 2 een deler van (2 – 1)! + 1? En dit is het totale bewijs! Hierboven hebben we een aanname gedaan, namelijk dat (G, × (mod p)) een groep is. We gaan dat hier ook niet bewijzen maar we kunnen wel eens even een kijkje nemen voor het geval ({1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, × (mod 11)) ofwel ons eigen voorbeeld met het priemgetal 11. Is de stelling van Wilson te gebruiken als test om te bepalen of een getal priem is? Het antwoord is: Ja. Als t een getal is en (t – 1)! + 1 ≡ 0 (mod t) dan is t een priemgetal, anders is t een samengesteld getal. Is de stelling van Wilson een praktische test om te bepalen of een getal priem is? Nee. En dit heeft te maken met het feit dat faculteiten de vervelende neiging hebben om snel heel groot te worden. Voorbeeld: Is 101 een priemgetal? Volgens de “Wilson-test”: is 101 een deler van (101 – 1)! + 1 ofwel is 101 een deler van 100! + 1. 100! + 1= 93.326.215.443.944.152.681.699.238.856.266.700.490.715.968.264.381.621.468.592.963.895.217.599.993.229.915.608.941.463.976.156.518.286.253.697.920.827.223.758.251.185.210.916.864.000.000.000.000.000.000.000.001 Getal gemaakt in Python import math Probeer zelf maar eens de deling van dit getal door 101. Met een gewone rekenmachine is dit niet te doen. Natuurlijk kun je dit wel in een programmeertaal als Python doen maar dan nog… En 101 is nog maar een klein getal. Om de vraag toch te beantwoorden kijken we even naar een andere methode, die we zelfs uit het hoofd kunnen doen: Als 101 een priemgetal is dan moet het niet deelbaar zijn door één van de priemgetallen kleiner of gelijk aan de wortel van 101 (zie Priemgetallen en Hoofdstelling van de rekenkunde). Welnu: De priemgetallen kleiner dan de wortel van 101 zijn: 2, 3, 5, 7 en voor de zekerheid 11. Numberphile 2: Wikipedia: Inleiding
Maar goed, we doen het ermee.
Het uitroepteken achter de 10 betekent “faculteit” en is niets anders dan de vermenigvuldiging van opeenvolgende getallen vanaf 1 tot en met 10.
In de kansberekening en statistiek betekent faculteit: Op hoeveel verschillende manieren je een bepaald aantal dingen kunt rangschikken.
Als je bijvoorbeeld 3 stiften hebt (rood (r), blauw (b) en zwart (z)) dan kun je deze op de volgende manieren naast elkaar leggen:Klokrekenen

9 (uur) + 5 (uur) = 14 (uur). Maar 14 komt niet op de klok voor. Dus moeten we hier 12 vanaf trekken: 14 (uur) – 12 (uur) = 2 (uur).
3 × 5 ≡ 1 (mod 2), hiermee bepaal je dus of een getal even of oneven is,
6 × 7 ≡ 0 (mod 6), wanneer er 0 uitkomt betekent het dus dat er geen rest is.
Welnu:Intuïtief bewijs voor de stelling
Welnu: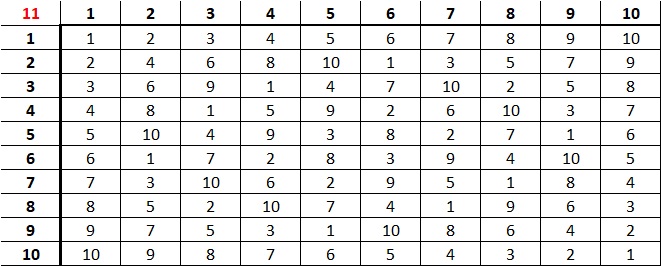
Dit is ook één van de voordelen van modulo-rekenen.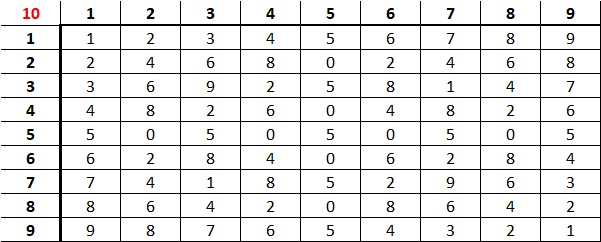
Groepen
Bewijs
Als a2 ≡ 1 (mod p) dan geldt: a2 – 1 = (a – 1)(a + 1) ≡ 0 (mod p). Maar omdat p priem is geldt dan dat a ≡ -1 (mod p) en p – 1 ≡ -1 (mod p) ofwel a ≡ 1 (mod p). Daaruit volgt dat 1 en p – 1 hun eigen inverse zijn.
[Als je hierboven voor a 1 of p – 1 invult, dan zie je dat het klopt, vul je voor a een ander getal in dat zie je dat het niet klopt].
(2 – 1)! + 1 = 1! + 1 = 1 + 1 = 2.
En 2 is inderdaad een deler van 2, dus dat klopt.
7 × 8 = 56 ≡ 1 (mod 11),
5 × 6 = 30 ≡ 8 (mod 11),
3 × 9 = 27 ≡ 5 (mod 11) (zie ook de mod-11-tabel hierboven)
(4 × 6) × 8 = 24 × 8 = 192 ≡ 5 (mod 11) en
4 × (6 × 8) = 4 × 48 = 192 ≡ 5 (mod 11) en dus
(4 × 6) × 8 = 4 × (6 × 8) = 192 ≡ 5 (mod 11)
1 × 8 = 8 × 1 = 8 ≡ 8 (mod 11),
1 × 30 = 30 × 1 = 30 ≡ 8 (mod 11)Tot slot
print(“{:,}”.format(math.factorial(100)+1).replace(“,”,”.”))
Het blijkt dat 101 niet deelbaar is door de bovengenoemde priemgetallen en dus is 101 zelf een priemgetal. Makkelijk toch?Bronnen