Inhoud
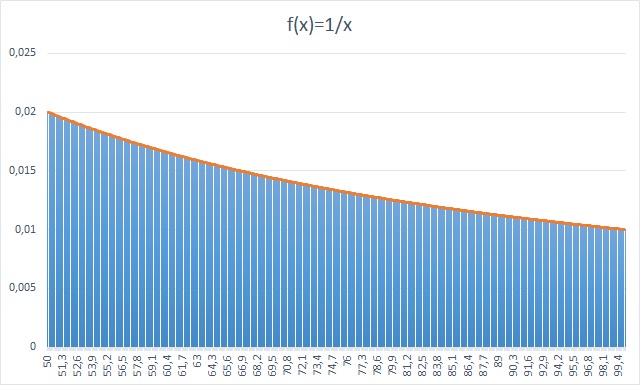
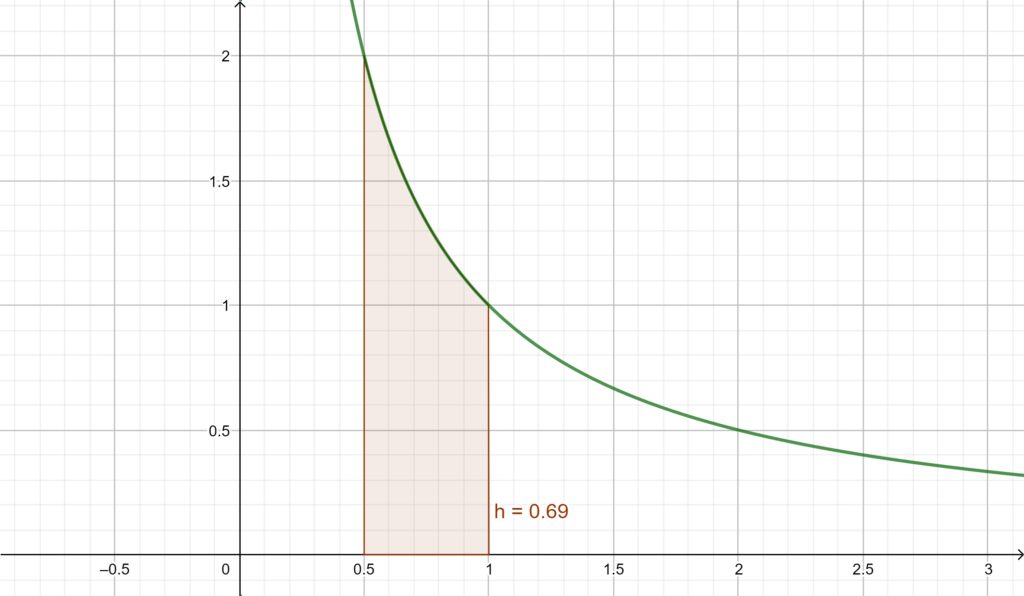
Er was eens, ergens in een ver weg gelegen land, een gevangenis met een wrede directeur. De gevangenis was vol. Op een goede dag kreeg de directeur van hoger hand te horen dat hij ruimte moest maken in de gevangenis om 100 nieuwe gevangenen te plaatsen. Nu kon hij natuurlijk de 100 braafste gevangenen vrij laten maar dat wilde hij niet zonder slag of stoot. Als nu alle 100 gevangenen hun eigen nummer hadden gevonden zouden ze allemaal worden vrijgelaten. Als alle gevangenen, zonder overleg vooraf, de ruimte betreden en op zoek gaan naar een doos waar hun nummer in zit, dan heeft iedere gevangene een kans van 1/2 om zijn kaartje te vinden. Maar omdat alle 100 gevangenen hun kaartje moeten vinden is de totale kans: ½100. Het ziet er slecht uit voor onze gevangenen. Er is echter een strategie te bedenken waarbij de kans dat ze allemaal worden vrij gelaten zo’n 31% is! Ze mogen vooraf wel met elkaar overleggen en het is dan te hopen dat er minimaal één gevangene is met het volgende briljante idee: Iedere gevangene opent als eerste de doos met zijn nummer erop en kijkt naar het nummer op het kaartje. Stel: Gevangene nummer 46 gaat de kamer binnen en opent doos 46. In doos 46 zit een kaartje met het nummer 73. Er worden dus zogenaamde loops gecreëerd: En daar zit de kracht van deze strategie in. Zo’n loop kan een lengte hebben van 1 (de gevangene vindt meteen zijn kaartje) t/m 100 (de gevangene heeft zijn kaartje niet gevonden). Door de willekeurige plaatsing van de kaartjes over de dozen zullen er ook loops van verschillende lengtes ontstaan. Wanneer een gevangene de eerste doos met zijn nummer erop opent dan zit die doos in de loop die uiteindelijk het nummer van de gevangene bevat. Dus de lengte van de loop is bepalend voor het succes van het vinden van het juiste getal. Als deze loop langer dan 50 is dan heeft de gevangene (en de rest) pech, anders hoera voor de gevangene. Als er een loop langer dan 50 is dan zullen er dus meer dan 50 gevangene hun kaartje niet vinden. We moeten dus gaan kijken naar de kans dat er, bij het willekeurig verdelen van de nummers over de dozen, er geen loops langer dan 50 zijn. Welnu: Op hoeveel manieren kun je 100 getallen verdelen over 100 dozen? Maar we hebben het hier over loops. Wat is nu de kans dat een willekeurige rangschikking van 100 dozen een loop met een lengte van 100 zal bevatten? Een kans is gedefinieerd als “het aantal gewenste resultaten” / “het totaal aantal mogelijkheden” en schrijven we als P(k). Dus onze kans is: P(L=100) = (100!/100) / 100! = 1/100 = 0,01 = 1%. Evenzo geldt: P(L=99) = 1/99 Samen: P(L>50) = 1/100 + 1/99 + 1/98 + … + 1/51 = 0,69. En omdat de totale kans niet groter dan 1 kan zijn geldt nu: P(L<=50) = 1 – P(L>50) = 1 – 0,69 = 0,31. Dus de hele groep van 100 gevangenen heeft een kans van 0,31, ofwel 31% om te slagen! En dat is heel wat meer dan de kans uit het begin van dit verhaal. Wat is de kans voor een groep van 1000 gevangenen, onder verder dezelfde omstandigheden? En P(L<=1.000.000) = 0,306853 Gaat dit naar een limiet? Ofwel hoe groot is P als L naar oneindig gaat? Laten we eens kijken naar de volgende grafiek: Dit is de grafiek van 1/x met 50 ≤ x ≤ 100 met een stapgrootte van 1. En deze grafiek “tendeert” naar de grafiek van 1/x als je x met steeds kleinere stapjes van 50 naar 100 laat lopen: Als we kijken naar de oppervlakte onder de grafiek van 1/x op het domein van <0,5; 1] dan krijgen we P(L>0,5): En dit is niets anders dan de bepaalde integraal: Dus P(gewenst) = 1 – ln(2) ≈ 0,306852 en dus gaat P inderdaad naar een limiet wanneer L naar oneindig gaat. Verreweg de beste bron: https://www.youtube.com/watch?v=iSNsgj1OCLA&ab_channel=VeritasiumInleiding
Dus bedacht hij een sadistische plan.Het sadistische plan


Had echter één of meer gevangenen niet hun eigen nummer gevonden dat zouden ze allemaal worden geëxecuteerd.
Nu is 2100 = 1.267.650.600.228.230.000.000.000.000.000 (één quintiljoen tweehonderdzevenenzestigduizend zeshonderdvijftig quadriljoen zeshonderd triljard tweehonderdachtentwintig triljoen tweehonderddertig biljard; zie ook Nomenclatuur getallen) en
½100 = 0,000000000000000000000000000000788860905221012.
Ik ben geneigd te zeggen dat deze kans kleiner dan “nihil” is…Goede strategie
Als dit nummer gelijk is aan zijn eigen nummer dan is hij klaar.
Als dit nummer een ander nummer is dan gaat hij naar de doos met het nummer dat op het kaartje staat en herhaalt hij deze procedure.
En dit mag hij dus maximaal 50 keer herhalen.
Hij gaat naar doos 73, opent deze en daar zit een kaartje met nummer 16 erin.
Hij gaat naar doos nummer 16 en daar zit een kaartje met nummer 46 erin; Hoera!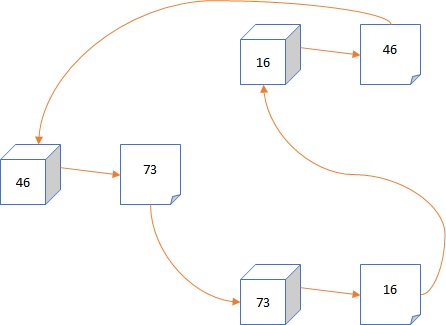
Het antwoord is: 100!. Het uitroepteken staat voor faculteit en betekent niets anders dan het product van 1 t/m 100 ofwel 1 × 2 × 3 × … × 98 × 99 × 100, en dat is best een groot getal.
Dus de loop 1 → 2 → 3 → … → 100 → 1 is hetzelfde als de loop 50 → 51 → 52 → … →49 → 50, etc. Er zijn hier dus 100 variaties op hetzelfde thema.
Het aantal unieke loops met een lengte van 100 is nu dus 100! / 100.
P(L=98) = 1/98
…
P(L=51) = 1/51Limiet
Dus wat is P(L<=500)? Dat is 1 – P(L>500) = 0,307352.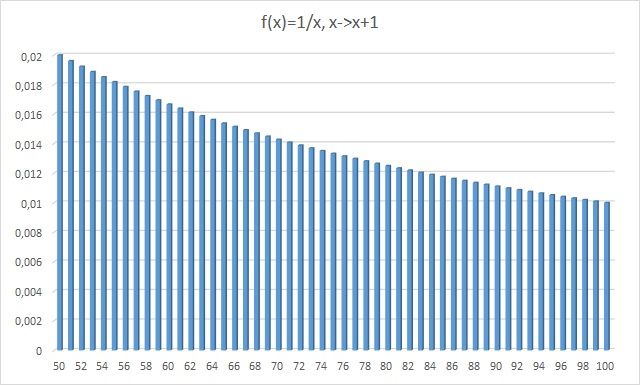
Bron
Onmogelijk gevangenen probleem
\int_{0,5}^{1}\frac{1}{x}=\int_{0,5}^{1}ln(x)dx=\left [ ln(x) \right ]_{0,5}^{1}=ln(1)-ln(0,5)=ln(\frac{1}{0,5})=ln(2)\approx 0,6931