Inhoud In dit artikel gaan we in op de formule van Tupper die in het Engels Tuppers Self-referential Formula (Tsrf) heet. We gaan kijken hoe deze formule eruit ziet en hoe deze werkt. Ook zullen we zien dat de formule versimpeld kan worden en zullen we een mogelijke verklaring geven voor het feit dat de plot van de formule eigenlijk op z’n kop staat. Maar eerst de formule zelf. Deze ziet er als volgt uit: En deze “indrukwekkende” formule plot zichzelf: Eerst even wat uitleg over de formule: De symbolen ⌊ en ⌋ betekenen dat de waarde die er tussen staat wordt afgerond naar het eerste gehele getal kleiner of gelijk aan de waarde. Dus ⌊3,14159265⌋ = 3; ⌊123.45⌋ = 123; ⌊15⌋ = 15; ⌊-56.89⌋ = -57. De mod(waarde, deler) functie bepaalt de rest die overblijft bij een gehele deling van waarde gedeeld door deling. Dus mod(15, 2) = 1, want 15/2 = 7 met een rest van 1 en mod(123, 17) = 4, want 123/17 = 7 met een rest van 4. De term “self-referential” is niet geheel terecht. Want de volgende plot is ook gemaakt met dezelfde formule: Wat is nu het geheim van deze twee verschillende plots? De plot staat in een grid van 106 breed bij 17 hoog. En alles wat je kunt “tekenen” in een grid van 106×17 kan door de formule van Tupper geplot worden. Je moet alleen de juiste K hebben. De K voor de eerste afbeelding is: En de K voor de tweede afbeelding is: Je ziet dat K grote getallen zijn. Het kleinst mogelijke getal voor K is 0 (een leeg grid), het grootst mogelijke getal voor K is 285793394306920833441610418092098634655629245793956098678773267955742373149291514664653927800704880150373913388423749690746007967577679155184353688551864105050094392601490879904551645289937784458453139617535910572704774231271588108092253680499408135958507227058036551719659148821493652464309016970613693109544906508636480672894494640559860467878289647366663850331954867463170600301178621010101029372654264171297982037231491311892858947537525986757827169736600317880446647247045504644272222656049350793825164158207773197137018282319809299349504 (een volledig gevuld grid). Een grid bestaat dus uit 106 vakjes breed bij 17 vakjes hoog: We gaan eerst kijken naar een simpel grid: De onderste 3 vakjes van de linker kolom zijn gevuld, dan is er een leeg vakje en daarboven zijn weer 2 vakjes gevuld. Om nu K te kunnen maken begin je in de meest linker kolom op de onderste rij. Wanneer een vakje gevuld is schrijf je een 1 neer, is het vakje leeg dan schrijf je een nul neer. Hierna ga je één vakje omhoog en herhaalt alles. In het voorbeeld hierboven krijg je dan: “111011” met daarachter allemaal “0”-en (1796 om precies te zijn). We hebben nu een binair (2-tallig) getal gemaakt. Het enige wat vervolgens moet gebeuren is deze omzetten naar een decimaal getal en dan vermenigvuldigen met 17 (de hoogte). En daar is dan de gezochte K. Hoe zet je een binair getal om naar een decimaal getal? We moeten dan eerst eens kijken hoe het decimale stelsel in elkaar zit. Ons 10-tallig systeem is een zogenaamd positioneel telsysteem. Dit betekent dat de positie waar een cijfer staat bepaalt wat de waarde is. Omdat we in een 10-tallig stelsel werken hebben we 10 verschillende symbolen nodig. Normaal noemen we deze symbolen cijfers. De cijfers zijn respectievelijk: 0, 1, 2, 3, 4, 5, 6, 7, 8 en 9. De posities lopen op van rechts naar links waarbij de meest rechter positie, positie 0 is. Voorbeeld: 345 betekent niets anders dan 3 × 102 + 4 × 101 + 5 × 100 = 3 × 100 + 4 × 10 + 5 × 1. Het voordeel van zo’n systeem is dat je met een bepaald aantal symbolen alle getallen kunt maken. In het hexadecimale- (16) tallig stelsel heb je dus 16 symbolen nodig: 0 t/m 9, A, B, C, D, E en F. Het grondtal is dan niet 10 maar 16. Dus 18C = 1 × 162 + 8 × 161 + 12 × 160 (decimaal) = 1 × 256 + 8 × 16 + 12 × 1 = 396 (decimaal). In het kort schrijven we: 18C|16 = 396|10 . En zo gaat het ook als we en binair (2-tallig) getal willen omzetten naar een decimaal getal: Het grondtal is 2 en we hebben maar 2 symbolen nodig: 0 en 1. Voorbeeld: 111011|2 = 1 × 25 + 1 × 24 + 1 × 23 +0 × 22 + 1 × 21 + 1 × 20 = 1 × 32 + 1 × 16 + 1 × 8 + 0 × 4 + 1 × 2 + 1 × 1 = 59|10 . In z’n algemeenheid heb je bij een n-tallig stelsel n symbolen nodig en is het grondtal n. Om nu van het getal K een plot te krijgen gaan we als volgt te werk: Het vakje linksonder heeft als coördinaten (0, K), dus de x=0 en de y=K. Haal deze door de formule (van Tupper) en kijk of de waarde groter of kleiner is dan 1/2. Is de waarde groter dan 1/2 dan kleur je het vakje met de coördinaten (0, K), anders laat je deze leeg. En zo loop je alle coördinaten door met y= K..K+16 en x= 0..106. Laten we nogmaals naar de formule kijken: Deze kunnen we ook anders schrijven: Ik maak hierbij gebruik van het feit dat x-a=1/xa. Merk ook op dat zowel de x-coördinaat als de y-coördinaat gehele getallen zijn. Dus ⌊x⌋ = x en hetzelfde geldt voor ⌊y⌋ = y. Hiermee kunnen we de formule iets versimpelen: En als we nu eens het eerste argument van de eerste mod-functie vervangen door q dan krijgen we: En dat is precies de expressie die bepaalt of een vakje gevuld wordt (≥1/2) of niet (<1/2). De “17” die in de formule 3 maal voorkomt is niets anders dan de hoogte van het grid. Als je een grid van 9 hoog wilt hebben dan verander je de “17” in een “9” in de formule. Je moet dan het decimale getal dat je verkrijgt van het binaire getal niet met 17 maar met 9 vermenigvuldigen om de juiste K te krijgen. Er zit een klein addertje onder het gras. Het is namelijk niet zo dat je één op één van het binaire getal dat het grid oplevert, via de omzetting naar K, en daarna weer terug naar het grid dezelfde figuur krijgt. Als we naar de K van de tupper-formule in het grid kijken dan is deze gemaakt vanuit het grid met de Tupper-formule. Maar als we deze K vervolgens gebruiken zoals de voorschriften hierboven allemaal vertellen dan krijgen we de volgende figuur: De figuur is 180° gedraaid (ofwel een keer horizontaal en een keer verticaal gespiegeld). Laten we dit eens nader bekijken. We gaan een figuurtje maken op een 4×4-grid (het grid hoeft overigens niet vierkant te zijn; het gaat om de hoogte): Als we van linksonder kolomsgewijs naar rechtsboven werken dan krijgen we het binaire getal: 1000 0001 0100 0010. En 1000 0001 0100 0010|2 = 33090|10. Om K te krijgen vermenigvuldigen we 33090 met 4 (de hoogte). We gaan nu alle (x, y) coördinaten in de formule invullen, waarbij x van 0 t/m 3 loopt en y van 132360 t/m 132363 loopt. We krijgen de volgende uitkomsten: En als we deze weer terug stoppen in het grid dan krijgen we: En dat is precies 180° gedraaid ten opzichte van het origineel! De software die van een bepaalde K een grid maakt moet dus als laatste stap de ontstane figuur 180° draaien. Waarschijnlijk heeft dit te maken met de software die Tupper gebruikte om zijn formule te testen. Bij veel programmeertalen is het nul-punt van een grafische canvas gesitueerd in de rechter-boven hoek. En dus verkreeg hij hetzelfde resultaat als de figuur die in eerste instantie in de grid was gemaakt. Matt Parker op Numberphile: https://www.youtube.com/watch?v=_s5RFgd59ao&ab_channel=Numberphile Jeff Tupper: https://www.dgp.toronto.edu/~mooncake/ Wikipedia: https://en.wikipedia.org/wiki/Tupper%27s_self-referential_formula Van grid naar K en omgekeerd: https://tuppers-formula.ovh/ Inleiding
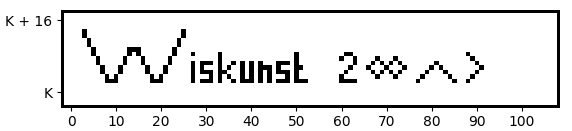
En de Engelse naam verklaart veel. Met de formule van Tupper is het mogelijk om deze formule zelf te plotten. Met andere woorden de formule plot zichzelf!Tsrf
Dat heeft alles met de waarde van K te maken. Deze K staat bij de y-as.
K=960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719
K=51784027487620646102193184148933876230751944022934402187433149411188275743475182598700003956893292165397446702483218550348206470030509304760297087275165449396945557723621785930165571749234454543750043411484431791204291907728496990920634032104394791213050905457868131925830674122548116185450382899598868742784520691849766030321450816373458375078299965059237605972138116295786599077470602908753630960761872765314803687864296922114670757992674736414046027829264901919064159143778058955195126662213876074162722999729671339015921467392Hoe komen we aan K?


Ben je bovenaan een kolom gekomen dan schuif je één kolom naar rechts en begint weer van onderaf aan. En zo doorloop je het gehele grid.Van binair naar decimaal
Elke positie vertegenwoordigt (heeft een waarde van) een macht van 10.
Dus positie 0 vertegenwoordigd een waarde van 100 = 1, positie 1 een waarde van 101 = 10, positie 2 een waarde van 102 = 100 enzovoort.
Deze waardes worden vermenigvuldigd met de waarde van de cijfers en vervolgens bij elkaar opgeteld.Van K naar de Tupper-plot
De formule nader bekeken
Rotatie
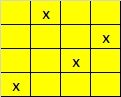
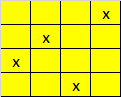
K is dus 132360.
x
y
T
0
132360
0
0
132361
1
0
132362
0
0
132363
0
1
132360
0
1
132361
0
1
132362
1
1
132363
0
2
132360
1
2
132361
0
2
132362
0
2
132363
0
3
132360
0
3
132361
0
3
132362
0
3
132363
1
Bronnen
Tuppers formule
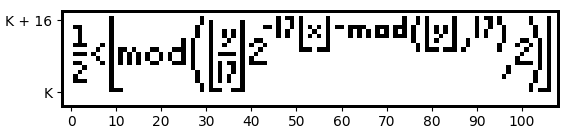
\frac{1}{2} < \left \lfloor mod\left ( \left \lfloor \frac{y}{17} \right \rfloor \cdot 2^{-17\left \lfloor x \right \rfloor-mod\left ( \left \lfloor y \right \rfloor,17 \right )} ,2 \right )\right \rfloor
\frac{1}{2} < \left \lfloor mod\left ( \left \lfloor \frac{y}{17} \right \rfloor \cdot 2^{-17\left \lfloor x \right \rfloor-mod\left ( \left \lfloor y \right \rfloor,17 \right )} ,2\right )\right \rfloor
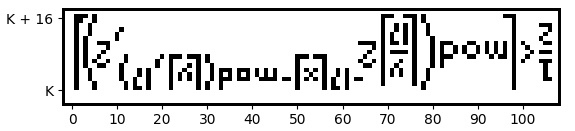
\frac{1}{2} < \left \lfloor mod\left ( \frac{\left \lfloor \frac{y}{17} \right \rfloor}{2^{17 \left \lfloor x \right \rfloor +mod\left ( \left \lfloor y \right \rfloor ,17 \right )}} ,2 \right )\right \rfloor
\frac{1}{2} < \left \lfloor mod\left ( \frac{\left \lfloor \frac{y}{17} \right \rfloor}{2^{17 x +mod\left ( y ,17 \right )}} ,2 \right )\right \rfloor
\frac{1}{2} < \left \lfloor mod\left ( q ,2 \right )\right \rfloor