Inhoud In deze aflevering gaan we kijken naar voorwaardelijke kansen en de stelling van Bayes. Dit zijn kansen waar van te voren al het één en ander bekend is. We zullen dit doen aan de hand van de volgende voorbeeld vragen: We zullen ook andere voorbeelden tegenkomen maar die zijn puur ter illustratie. In een eerdere aflevering wordt al het één en ander uitgelegd over kansberekening en ik raad de lezer aan deze aflevering nog eens na te lezen. De wiskundige definitie van kans luidt: De P staat voor Probability (=kans) en # staat voor aantal. Dus een kans is niets anders dan het quotiënt van het aantal mogelijke positieve uitkomsten en het totaal aantal uitkomsten. De meeste voorbeelden hebben betrekking op dobbelstenen, munten en knikkers, dus vooruit maar… Voorbeelden: Wat is de kans op een 3 als je 1 keer gooit met een (normale) dobbelsteen? Wat is de kans dat je kop gooit als je 1 keer een muntje op werpt? In een vaas zitten 3 roden, 4 groene en 5 blauwe knikkers. Hoe groot is de kans dat je bij een blinde trekking een groene knikker hebt? Een kans is altijd een getal tussen de 0 en de 1. Dit volgt rechtstreeks uit de definitie, immers is de teller altijd kleiner (of gelijk) aan de noemer. Een kans kan echter ook de waarde 0 zelf of 1 zelf hebben. Een kans van 0 betekent dat iets niet kan voorkomen, bijvoorbeeld de kans op 7 ogen bij het werpen van 1 maal een normale dobbelsteen: Een kans van 1 betekent dat iets altijd zal voorkomen, bijvoorbeeld de kans dat je een rode knikker trekt uit een vaas met (alleen) 10 rode knikkers: P(rood) = 10/10 = 1. Ook geldt dat de kans op A + de kans op niet-A gelijk is aan 1. De notatie -A betekent dus niet-A. En soms is het makkelijker om niet-A te bepalen dan A zelf en dan kun je dus P(A) = 1 – P(-A) gebruiken. Bij onafhankelijke kansen heeft de kans op het ene niets te maken met de kans op het andere. Voorbeeld: Wat is de kans dat je kop gooit bij het gooien van een muntje en een 6 gooit bij het werpen met een dobbelsteen? Bij afhankelijke kansen is de kans op het ene afhankelijk van de kans op het andere. Je rekent eerst de kans van het ene uit, daarna de kans op het andere en vermenigvuldigt vervolgens die kansen. Voorbeeld: Wat is de kans dat je 2 keer kop gooit bij het gooien van 2x een muntje? Je kunt dit ook als volgt bekijken: Je kunt kansen ook door middel van zogenaamde Venndiagrammen weergeven. En dat is handig om voorwaardelijke kansen te beschouwen. De kansen die we tot nog toe hebben besproken zijn allemaal als volgt in een Venndiagram te vatten: De U staat voor het universum. A is de verzameling waar het over gaat; dus bv. de ogen van een dobbelsteen, een vaas met knikkers, en muntje etc. Een verzameling in de wiskunde is een “groep” met elementen die op de één of andere manier bij elkaar horen. Ieder element komt maar 1 keer voor en alle elementen staan tussen accolades; {…}. Dus, bijvoorbeeld, de kans op een 3 bij het gooien met 1 dobbelsteen wordt dan: Waarbij A = {1, 2, 3, 4, 5, 6}. Hebben we nu twee verzamelingen dan kan een Venndiagram meerdere vormen aannemen. De twee verzamelingen hebben geen enkele overeenkomst: Bijvoorbeeld: A = {1, 2, 3} en B = { 4, 5} Er kunnen echter ook overlappingen plaats vinden en daarbij zijn een aantal varianten van belang. Bij de vereniging van twee verzamelingen neem je alle elementen van de verzamelingen. Voorbeeld: A = { 1, 2, 3, 4} en B = { 3, 4, 5, 6, 7, 8}. Het symbool ∪ betekent: Vereniging. Merk op dat de elementen maar 1 keer voorkomen in de vereniging. In een Venndiagram kan dat er als volgt uitzien: Bij de doorsnede van twee verzamelingen zitten alleen die elementen die zowel in A als in B zitten. Voorbeeld: A = { 1, 2, 3, 4} en B = { 3, 4, 5, 6, 7, 8}. Het symbool ∩ betekent: Doorsnede. In een Venndiagram kan dat er als volgt uitzien: We gaan nu kijken naar de kans dat iets gebeurt terwijl we al weten dat iets anders is gebeurd. De notatie luidt: P(A|B) en betekent: De kans op A gegeven B. Het symbool | betekent dus: “gegeven”. En daar is in de wiskunde ook een formele definitie van: Dus de kans op A gegeven B is de kans op de doorsnede van A en B gedeeld door de kans op B. Als voorbeeld gaan we eens kijken naar de eerste drie vragen. i) Wat is de kans dat een echtpaar met 2 kinderen 2 dochters heeft? Hier hebben we de bovenstaande formule nog niet nodig. We kijken gewoon naar de mogelijkheden van het hebben van 2 kinderen: zz, zd, dz, dd. De z staat natuurlijk voor zoon en de d voor dochter. We zoeken de combinatie dd en die komt 1 keer voor in de 4 mogelijkheden. Gebruikmakend van de standaard formule voor kans krijgen we dus: P(dd) = 1/4. ii) Wat is de kans dat een echtpaar met 2 kinderen 2 dochters heeft als je weet dat één van de kinderen een dochter is? Nu is de situatie anders. De vraag op de kans op twee dochters is weliswaar hetzelfde maar we hebben meer informatie. We weten nu dat minstens één van hun kinderen een dochter is. Dit betekent dat het aantal mogelijkheden, ten opzichte van de vorige vraag, 1 is afgenomen, nl: zd, dz, dd. De zz is nu niet meer opportuun. Dit betekent dat de kans op twee dochters nog maar 1/3 is, ofwel P(dd)=1/3. Kunnen we dit resultaat nu ook verkrijgen door onze nieuwe formule? Welnu: A = {dd} en B = {zz, zd, dz, dd}. P(A ∩ B) = 1/4 (dd komt maar 1 keer voor in B) P(B) betekent de kans op minstens 1 dochter en is: P(B) = 3/4 (zd, dz of dd). In de formule geeft dit: P(A|B) = (1/4) / (3/4) = 1/3. Het klopt! iii) Wat is de kans dat een echtpaar met 2 kinderen 2 dochters heeft als je weet dat hun oudste kind een dochter is? Deze lijkt heel erg op vraag ii) maar is subtiel toch anders. We weten niet alleen dat ze minstens 1 dochter hebben maar we weten ook welk kind dat is, namelijk de oudste. Dus P(B) is nu 2/4 = 1/2. Invullen in de formule: P(A|B) = (1/4) / (1/2) = 1/2. Kun je deze kans nu zelf op een andere manier bepalen? Antwoord We zoeken naar dd en we weten dat de oudste een d is. Er zijn nu dus nog maar twee mogelijkheden om uit te kiezen, namelijk: zd en dd. iii.i) En nu de doordenker: Wat is de kans dat een echtpaar met 2 kinderen een zoon en een dochter heeft wanneer je weet dat ze een zoon hebben die op een dinsdag is geboren? Het antwoord lijkt voor de hand te liggen. De verzameling mogelijkheden zijn {zz, zd, dz} waarvan {zd, dz} voldoet, dus 2 van de 3 en dus is de kans 2/3. Maar dat is niet juist! Kun je zelf bedenken waarom dit zo is (zonder gebruik van de formule te maken)? Antwoord De clou zit hem hier in het aantal mogelijkheden. We hebben ook hier weer te maken met meer informatie die we zullen moeten meenemen in de berekening. Het totale aantal mogelijkheden is 27, waarvan er 14 voldoen. Je moet rekening houden met het feit dat een zoon geboren is op een dinsdag. In onderstaande tabel staan alle mogelijkheden op 2 kinderen waarvan 1 zoon geboren is op een dinsdag: En hierin komt maar 1 keer de combinatie z2z2 voor (of eigenlijk vallen deze mogelijkheden z2z2 en z2z2 samen). Je weet namelijk niet welke zoon er op een dinsdag geboren is alleen dat er één op een dinsdag geboren is. Het totaal aantal mogelijkheden is dus 27. Daarvan zijn er 14 waarin een dochter voorkomt. Dus de kans op een dochter als je weet dat de zoon geboren is op een dinsdag is 14/27. En nu de volgende vraag: iv) Het percentage van alle volwassen mannelijke alcoholisten is 2,25%. Wat is de kans dat een man alcoholist is? Deze lijkt op het oog heel simpel te beantwoorden, maar dat is het niet. Je bent wellicht geneigd te zeggen dat deze kans 0,0225 (2,25%) is maar dan ga je voorbij aan het feit dat er niet alleen maar mannen op deze aarde zijn! We moeten A en B derhalve precies definiëren. A=alcoholist Dan P(A∩B) = 0,0225 en P(B)=0,5 (er vanuit gaand dat de populatie volwassenen uit 50% mannen en 50% vrouwen bestaat). Dan krijgen we: P(A|B) = 0,0225 / 0,5 = 0,045 ofwel 4,5% kans dat een man alcoholist is. Voor vraag v) en vi) hebben we niet meer genoeg aan de formule voor voorwaardelijk kans zoals in de vorige paragraaf is besproken. We moeten de formule uitbreiden. Merk op dat: A∩B = B∩A. Nu gaan we kijken naar P(A|B) en P(B|A). Maar omdat A∩B = B∩A geldt ook P(A∩B) = P(B∩A). Dus geldt: Maar dan ook: Dus in het kort: En deze laatste formule is vernoemd naar Bayes en heet dus de formule van Bayes. En deze formule gaan we gebruiken om vraag v) te beantwoorden. v) Ziekte X komt bij 0,1% van de populatie voor. Je hebt dus een test gedaan en die was positief. Vanuit de gegevens ben je ongetwijfeld overtuigd dat je nu 99% zeker bent dat je ziekte X hebt. De rest van de gegevens moeten ook worden meegenomen. Wat zeggen al die gegevens nu eigenlijk. Laten we A vertalen met “Je hebt de ziekte X” en B met “Je testte positief”. Dus A = Je hebt ziekte X en En als we nu verder kijken naar alle componenten van de formule van Bayes, dan krijgen we: P(A|B): de kans op ziekte X bij een positieve test P(A|B) is wat we willen weten. P(A) is gegeven en bedraagt 0,001 (0,1%). P(B|A) is ook gegeven en bedraagt 0,99 (99%). P(B) is wat lastiger te bepalen. We moeten deze uitsplitsen in twee (onafhankelijke) delen: deel 1: De kans op ziekte X zonder test en de kans op een positieve test als je ziekte X hebt, deel 2: De kans dat je ziekte X niet hebt en de kans dat je ziekte X niet hebt terwijl de test positief is. De kans op deel 1 kun je als volgt schrijven: P(A) × P(B|A) = 0,001 × 0,99 = 0,00099. De kans op deel 2 kun je als volgt schrijven: P(-A) × P(B|-A) = 0,999 × 0,01 = 0,00999. Omdat deel 1 en deel 2 onafhankelijk zijn moeten we deze twee bij elkaar optellen. We krijgen nu dus: En als we alle getalletjes invullen dan krijgen we: En dit is wellicht een verrassend resultaat. Wanneer je een positieve test hebt dan heb je maar zo’n 9% kans dat je de ziekte X ook daadwerkelijk hebt. En als je nog eens goed naar de gegevens kijkt is dit zelfs intuïtief in te zien. Wanneer de populatie 1000 mensen betreft dan is er precies 1 mens met de ziekte X. Een overbekend verhaal over een quiz waarin de kandidaat voor 3 dichte deuren staat waarachter 1 van die deuren een mooie prijs zit terwijl achter de andere deuren niets zit. De vraag is: Moet de kandidaat inderdaad van deur wisselen of juist niet of maakt het niets uit? De intuïtie zal zeggen dat de kandidaat nu een kans van 1 op 2, ofwel 1/2, heeft op de prijs, en dat het dus niet uitmaakt welke deur wordt gekozen. De meeste mensen zullen dan ook geneigd zijn te zeggen dat het dus niets uitmaakt. Maar niets is minder waar! De kandidaat verhoogt zijn kansen door juist wel te wisselen van deur. Hij verdubbelt zijn kans zelfs door te wisselen. Met een tabel is dit goed te illustreren: Uit deze tabel blijkt dat wanneer het spel volledig wordt gespeeld de kandidaat 3 van de 9 keer wint als hij/zij niet wisselt en maar liefst 6 (2x zoveel dus) van de 9 keer wint als hij/zij wel wisselt. Maf hè? Maar wat zegt Bayes ervan? We moeten eerst wat zaken benoemen en berekenen. Mn zegt dat de mooie (M) prijs achter deur n (1, 2 of 3) staat. Qn zegt dat de quizmaster (Q) deur n opent. We gaan er vanuit dat de producent van de quiz geen speciale voorkeur heeft om de mooie prijs achter een specifieke deur te willen plaatsen en dus geldt: P(M1) = P(M2) = P(M3) = 1/3. Stel dat de kandidaat in eerste instantie deur 1 heeft gekozen. Dan gelden voor de quizmaster de volgende kansen: P(Q2|M1) = 1/2; de kans dat de quizmaster deur 2 opent als de prijs achter deur 1 zit; Stel de quizmaster opent deur 3 (en daar staat dus niets achter). Wat is nu de kans op de mooie prijs achter deur 2? We moeten dus P(M2|Q3) berekenen. Er geldt: Getalletjes invullen geeft: Als je toch nog twijfels hebt over bovenstaande tegen-intuïtieve antwoord dan bevind je je in goed gezelschap. Bayes leefde van 1702 tot en met 1771 en was van Britse afkomst. Hij was predikant en wiskundige en in deze laatste hoedanigheid hield hij zicht bezig met kansberekening. Hij vroeg zich op enig moment af hoe de uitkomst van een experiment geschat kan worden als je de resultaten van eerdere experimenten gaat meewegen. Hij deed dit door steeds een propje papier achter zicht te gooien op een tafel die achter hem stond en dan aan zijn secretaresse te vragen waar het propje terecht was gekomen ten opzichte van zijn vorige gegooide propje. Dit experiment werkte hij vervolgens in één van zijn vele geschriften uit, maar publiceerde dit nooit. Pas na zijn dood vond een huisvriend, R. Price, deze aantekeningen en publiceerde hierover. https://www.youtube.com/watch?v=OByl4RJxnKA&ab_channel=TheOrganicChemistryTutor https://nl.wikipedia.org/wiki/Driedeurenprobleem https://nl.wikipedia.org/wiki/Thomas_Bayes Laatst gewijzigd op 26 januari 2026.Inleiding
Een test om ziekte X vast te stellen is voor 99% betrouwbaar.
Deze zelfde test heeft het in 1% van de positieve uitkomsten fout.
Hoe groot is de kans dat je ziekte X hebt als je een positieve test hebt?Definitie
Een dobbelsteen heeft 6 mogelijke uitkomsten (1 t/m 6) en één daarvan willen we hebben, namelijk 3. Dus is de kans:
P(3 ogen) = 1/6.
Een munt heeft 2 zijden, nl. kop en munt. We willen kop hebben dus is de kans:
P(kop) = 1/2.
Er zitten totaal 12 knikker in de vaas, 4 daarvan zijn groen en dus is de kans:
P(groen) = 4/12 = 1/3.Interval [0, 1]
P(7 ogen) = 0/6 = 0.
Dus P(A) + P(-A) = 1 ⇔ P(A) = 1 – P(-A).Onafhankelijke kansen
Je bepaalt afzonderlijk de kans op het ene en het andere en telt daarna de kansen bij elkaar op.
Er zijn hier twee handelingen die niets met elkaar te maken hebben. Ze zijn dus onafhankelijk van elkaar. Dus we moeten nu de twee kansen bepalen en deze dan bij elkaar optellen:
P(kop) = 1/2, P(6 ogen) = 1/6, P(kop ∨ 6 ogen) = 1/2 + 1/6 = 4/6 = 2/3.
Het symbool ∨ betekent: of.Afhankelijke kansen
Dit betekent dat je de eerste keer kop moet gooien (P(kop)=1/2) en de tweede keer ook kop moet gooien (P(kop)=1/2). Deze twee kansen moeten nu met elkaar vermenigvuldigd worden, dus:
P(kop ∧ kop) = 1/2 × 1/2 = 1/4.
Het symbool ∧ betekent: en.
De mogelijke uitkomsten van 2 x gooien met een munt zijn: mm, km, mk, kk (waarbij k staat voor kop en m voor munt). Er zijn dus 4 mogelijke uitkomsten. We willen nu kk hebben en dat is 1 van de vier mogelijke uitkomsten, dus P(kk) = 1/4.Verzamelingen
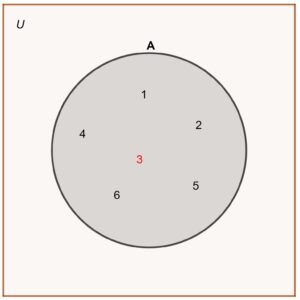
Disjuncte verzamelingen
Vereniging
Dan is de vereniging van A en B: A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}.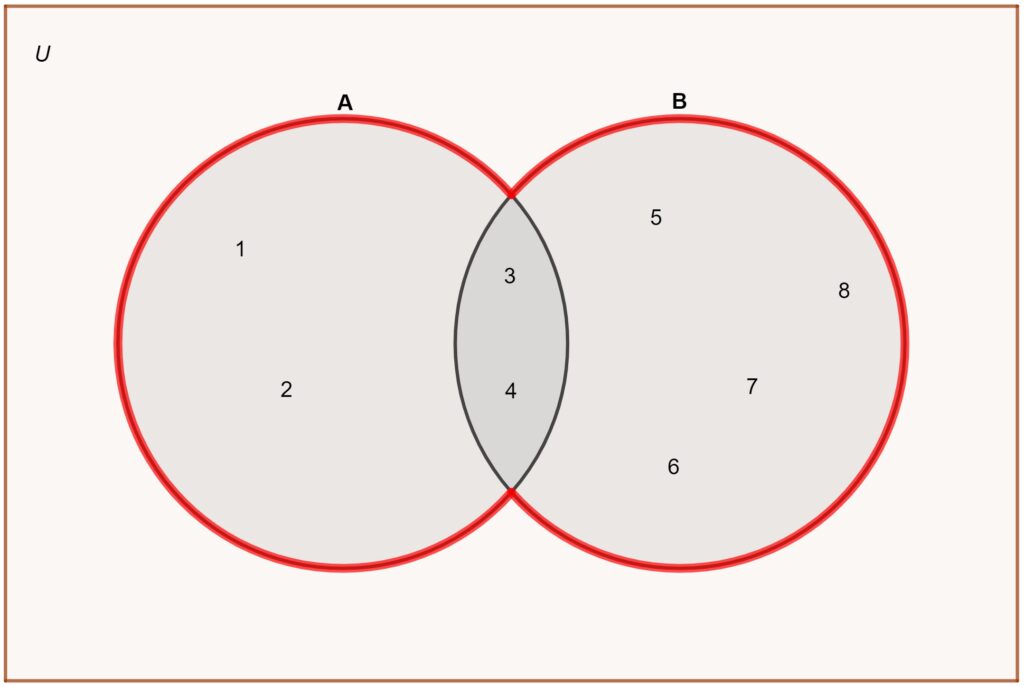
Doorsnede
Dan is de doorsnede van A en B: A ∩ B = {3, 4}.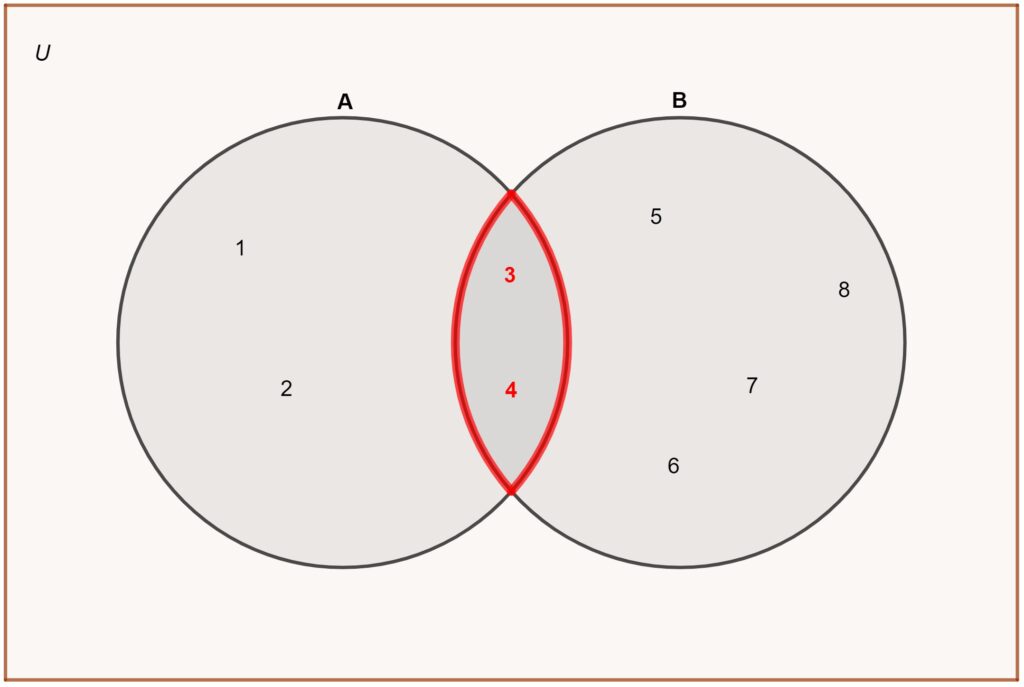
Voorwaardelijke kansen
We moeten dan goed definiëren wat de verzamelingen A en B zijn.
En daar dd maar 1 keer voorkomt in {zd, dd} is de kans dus 1/2.
Het antwoord is: De kans is 14/27 (≈0,518 of 51,8%).
1=ma, 2=di, 3=wo, 4=do, 5=vr, 6=za, 7=zo
zz
zd
dz
z1z2
z2z1
z2d1
d1z2
z2z2
z2d2
d2z2
z3z2
z2z3
z2d3
d3z2
z4z2
z2z4
z2d4
d4z2
z5z2
z2z5
z2d5
d5z2
z6z2
z2z5
z2d6
d5z2
z7z2
z2z7
z2d7
d6z2
B=manBayes
Een test om ziekte X vast te stellen is voor 99% betrouwbaar.
Deze zelfde test heeft het in 1% van de positieve uitkomsten fout.
Hoe groot is de kans dat je ziekte X hebt als je een positieve test hebt?
Maar niets is minder waar!
B = Je testte positief.
P(A): de kans op de ziekte X zonder test
P(B|A): kans op een positieve test als je de ziekte hebt
P(B): totale kans op een positieve test.
Er worden echter 10 mensen positief getest terwijl ze de ziekte X niet hebben.
De kans is dus ongeveer 1/11 (≈0,09) dat je bij een positieve test ook daadwerkelijk ziekte X hebt.Monty Hall
De kandidaat mag één deur kiezen, maar nog niet openen. De quizmaster opent nu één van de andere deuren waarachter geen prijs zit.
De kandidaat mag nu nog van deur wisselen (waarbij de kandidaat uiteraard niet voor de inmiddels open deur zal kiezen).
Kandidaat kiest deur
Prijs achter deur
Quizmaster opent deur
Kandidaat wisselt niet
Kandidaat wisselt wel
1
1
2 of 3
win
verlies
1
2
3
verlies
win
1
3
2
verlies
win
2
1
3
verlies
win
2
2
1 of 3
win
verlies
2
3
1
verlies
win
3
1
2
verlies
win
3
2
1
verlies
win
3
3
1 of 2
win
verlies
3/9 wins
6/9 wins
P(Q3|M1) = 1/2; de kans dat de quizmaster deur 3 opent als de prijs achter deur 1 zit;
P(Q2|M2) = 0; de kans dat de quizmaster deur 2 opent als de prijs achter deur 2 zit;
P(Q3|M2) = 1; de kans dat de quizmaster deur 3 opent als de prijs achter deur 2 zit;
P(Q2|M3) = 1; de kans dat de quizmaster deur 2 opent als de prijs achter deur 3 zit;
P(Q3|M3) = 0; de kans dat de quizmaster deur 3 opent als de prijs achter deur 3 zit.
De grote Paul Erdös had zelf veel moeite met dit “probleem”. Pas nadat hij een simulatie had gezien was hij overtuigd van het resultaat.Korte biografie
Thomas Bayes
Deze publicatie werd gelezen door, de eveneens zeer beroemde wiskundige, Laplace, die uit deze publicatie de formule van Bayes destilleerde.Bronnen
https://www.youtube.com/watch?v=R13BD8qKeTg&ab_channel=Veritasium
https://www.youtube.com/watch?v=HZGCoVF3YvM&ab_channel=3Blue1Brown
https://www.youtube.com/watch?v=VuskwsIW02M&ab_channel=Dr.TreforBazett
https://statisticsbyjim.com/fun/monty-hall-problem/
Voorwaardelijke kansen – Bayes
P(k)=\frac{\#positieve\;uitkomsten}{\#mogelijke\;uitkomsten}
P(A|B)=\frac{P(A\cap B)}{P(B)}
P(A|B)=\frac{P(A\cap B)}{P(B)}
P(B|A)=\frac{P(B\cap A)}{P(A)}
P(B\cap A)=P(B|A)\cdot P(A)=P(A\cap B)
P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{P(B\cap A)}{P(B)}=\frac{P(B|A)\cdot P(A)}{P(B)}
P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}
P(A|B)=\frac{P(B|A)\cdot P(A)}{P(B)}=\frac{P(B|A)\cdot P(B)}{P(A)\cdot P(B|A)+P(-A)\cdot P(B|-A)}
P(A|B)=\frac{0,99\cdot 0,001}{0,001\cdot 0,99+0,999\cdot 0,01}=\frac{0,00099}{0,01098}=0,0902
P(M_{2}|Q_{3})=\frac{P(Q_{3}|M_{2})\cdot P(M_{2})}{P(Q_{3}|M_{1})\cdot P(M_{1})+P(Q_{3}|M_{2})\cdot P(M_{2})+P(Q_{3}|M_{3})\cdot P(M_{3})}
P(M_{2}|Q_{3})=\frac{1\cdot \frac{1}{3}}{\frac{1}{2}\cdot \frac{1}{3}+1\cdot \frac{1}{3}+0\cdot \frac{1}{3}}=\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}