In ieder axiomatisch stelsel bestaat een definitie van bewijs. Niet van waarheid!
Gödel
Deze aflevering gaat over wiskundige bewijzen. Ik zal eerst uitleggen wat we verstaan onder een wiskundig bewijs. Vervolgens geef ik een paar relatief simpele bewijzen waaronder twee klassieke bewijzen.
Inleiding
Wiskunde is niets anders dan een spel. Een spel heeft regels, en wiskunde vormt hierop geen uitzondering. Het spel wordt als volgt gespeeld: Neem een aantal uitgangspunten, wiskundigen noemen dit axioma’s, en leidt daar nieuwe regels, stellingen genoemd, vanaf en toets tot slot deze regels weer met de axioma’s of met eerder getoetste stellingen. Deze laatste stap noemen wiskundigen “bewijzen”.
Historie
Wanneer je kijkt naar de historie van de wiskunde, dan kun je zien dat de wiskunde in de loop der tijden steeds uitgebreider, en misschien ook wel moeilijker is geworden. Vooral vanaf de middeleeuwen werd de hoeveelheid wiskundige kennis zo omvangrijk dat men behoefte kreeg aan zogenaamde formele systemen. Dat zijn systemen die netjes zijn opgebouwd uit axioma’s en stellingen die ook bewezen dienden te worden. Het hoogtepunt van deze ontwikkeling vond ik het begin van de twintigste eeuw plaats. Twee grote namen uit laatst genoemde periode zijn Cantor (zie ook het artikel Oneindig) en Gödel. Deze laatste heeft bewezen dat ieder wiskundig systeem onoverkomelijk fouten in zich heeft, of met andere woorden, dat er geen volledig juist formeel wiskundig systeem bestaat. Ieder systeem herbergt paradoxen in zich. Dat laatste leidt overigens vaak tot nieuwe wiskundige ontdekkingen. Met het voortschrijden der tijden zie je ook dat de bewijzen ingewikkelder worden.
Soorten bewijzen
Rechttoe/rechtaan
Wanneer een stelling rechtstreeks vanuit de axioma’s en/of eerder bewezen stellingen bewezen wordt dan noemen we dat een rechttoe/rechtaan bewijs.
Bewijs uit het ongerijmde
Er zijn gevallen waarbij een rechttoe/rechtaan bewijs niet lukt. Je kunt dan je toevlucht nemen tot een bewijs uit het ongerijmde. De te bewijzen stelling ga je ontkennen en bewijst vervolgens dat dit tot een tegenspraak leidt. Daar wiskunde sterk binair georiënteerd is (iets is waar of iets is onwaar), bewijs je daarmee de originele stelling.
Bewijs met volledige inductie
Dit is een eigenaardig type bewijs waar dan ook nog steeds discussie over wordt gevoerd. De meeste wiskundigen accepteren dit type bewijs heden ten dage.
Je kunt het bewijs met volledige inductie het best vergelijken met een rij dominostenen. Je gooit de eerste omver en wanneer je kunt aantonen dat de laatste zal vallen dan is het bewijs rond. Om te bewijzen dat de laatste valt gaat men er vanuit dat er nog een steentje meer is. Vervolgens zegt men dat de, nu op één na laatste, steen valt en bewijst dat daardoor ook de laatste steen valt. Wanneer dat lukt is het bewijs rond.
Het vreemde zit hem in het feit dat je datgene wat je moet bewijzen als gegeven in je bewijs wordt gebruikt; daar wordt dan ook de discussie over gevoerd.
Combinatie
In wat grotere, langere bewijzen komen ook combinaties van bovenstaande methoden voor.
Vaak moeten stellingen worden opgedeeld in meerdere stukken die vervolgens allemaal bewezen dienen te worden.
Voorbeelden
De verzameling der natuurlijke getallen is oneindig
Stel er zijn eindig veel natuurlijke getallen. Dan is er een grootste, zeg N. Het is makkelijk na te gaan dat ik hier 1 bij op kan tellen, dus N+1. En N+1 is groter dan N.
De conclusie moet dus zijn dat er geen grootste getal bestaat en derhalve is de verzameling der natuurlijke getallen oneindig.
Dit is dus een bewijs uit het ongerijmde waarbij je er vanuit gaat dat een verzameling eindig of oneindig is.
De som van 1 t/m n = ½n(n+1)
Dit is een bewijs met volledige inductie.
De som van de (natuurlijke) getallen van 1 t/m n wordt in de wiskunde aangegeven met het symbool ∑, de Griekse hoofdletter S en wel als volgt:
Dit betekent niets anders dan de som van alle k’s die lopen vanaf 1 t/m n.
We moeten dus bewijzen:
Bewijs:
Stap 1: Toon aan dat de stelling waar is voor n=1:
Stap 2: De inductie stap. Ga er vanuit dat de stelling waar is dan moet nu worden bewezen:
Gebruik nu inductie:
Zoals je ziet is de eerste stap waar en is a) gelijk aan b), waarmee, volgens inductie, de stelling bewezen is.
De stelling van Pythagoras
Dit is misschien wel de meest bewezen stelling ter wereld.
Hieronder dus één van de vele varianten.
De stelling van Pythagoras geldt in een rechthoekige driehoek, dus één van de hoeken is 90°, en luidt dan dat a2+b2=c2, waarbij a en b de rechthoekzijden zijn en c de schuine zijde ofwel de hypotenusa is:
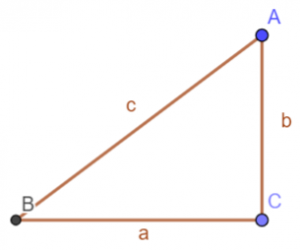
Bewijs:
Bestudeer onderstaande afbeelding aandachtig:
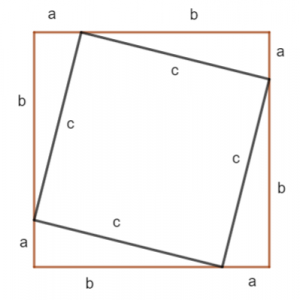
Er zijn twee vierkanten te onderscheiden: Eén met zijde (a+b) en één met zijde c.
Verder zijn er vier rechthoekige driehoeken abc, waarvan ∠cab (hoek a dus) 90° is, a en b de rechthoekzijden zijn en c de hypotenusa.
We gaan nu de oppervlakte van het ingeschreven vierkant (met zijde c) op twee manieren bepalen:
- Oppervlakte ingeschreven vierkant (met zijde c);
- Oppervlakte ingeschreven vierkant = Oppervlakte buitenste vierkant (met zijde a+b) – 4 x Oppervlakte driehoek abc.
De oppervlakte van 1. is: c x c = c2.
De oppervlakte van 2. is: (a+b)2 – 4 x ½ab = a2 + 2ab + b2 – 2ab = a2 + b2.
Het moge duidelijk zijn dan 1. en 2. aan elkaar gelijk moeten zijn en dus: a2 +b2 = c2.
De ABC-formule
De ABC-formule, ook wel wortel-formule genoemd, wordt gebruikt om de oplossingen van 2e-graads vergelijkingen mee te berekenen.
Een 2e-graads vergelijking heeft als algemene vorm: ax2+bx+c. Wanneer deze op nul gesteld wordt kunnen de oplossingen met behulp van de ABC-formule worden gevonden.
De ABC-formule luidt:
De x1 en x2 betekenen niets anders dan dat een 2e-graads vergelijking 2 oplossingen heeft. De ene met in de teller een plus-teken en de ander met in de teller een min-teken, vandaar de ±.
Om deze formule te bewijzen is een (simpele) afleiding voldoende. Het enige dat beheerst moet worden is het afsplitsen van een kwadraat, zoals u ooit op de middelbare school heeft geleerd, en het toepassen van een trucje.
Bewijs:
1) Ga uit van ax2 + bx + c = 0.
2) (truc) Vermenigvuldig beide zijden met 4a: 4a2x2 + 4abx + 4ac = 0.
3) Kwadraat afsplitsen levert op: (2ax + b)2 – b2 + 4ac = 0.
4) Losse termen (zonder x) naar rechts brengen: (2ax + b)2 = b2 – 4ac.
5) Van beide zijden de wortel trekken:
6) Losse termen naar rechts brengen:
7) Beide zijden door 2a delen:
En hier hebben we dus onze ABC-formule.
Tot slot nog even wat nadere uitleg over stap 3), het kwadraat afsplitsen.
Bij het kwadraat afsplitsen kijken we eerst naar de termen met een x erin en proberen die in de vorm (ax+b)2 te krijgen. In dit geval wordt dat: Kijk naar 4a2x2+4abx. Het is niet zo ingewikkeld om daar nu (2ax+b)2 van te maken. Werken we nu echter de haakjes weer weg, dan blijkt dat we een b2 te veel hebben, vandaar dat bij stap 3) er een -b2 is bijgekomen.
Er zijn oneindig veel priemgetallen
Een echte klassieker uit de oudheid. Het volgende bewijs uit het ongerijmde is reeds door Euclides geleverd.
Een priemgetal is een geheel getal met precies 2 (verschillende) gehele delers, namelijk 1 en zichzelf.
De eerste 11 priemgetallen zijn: 2, 3, 5, 7, 11, 13, 17, 19, 23, 27 en 31.
Het bewijs:
Stel er zijn eindig veel priemgetallen.
Dan kan ik ze allemaal op een rijtje zetten: 2, 3, 5, 7, 11, …, P, waarbij P dus het grootste priemgetal is.
Maak nu eens een nieuw getal G als volgt: G = 2 x 3 x 5 x 7 x 11 x … x P + 1, dus G is het product van alle priemgetallen 2 t/m P verhoogd met 1.
Nu blijkt dat G niet deelbaar is door 2, want de rest is 1. G is ook niet deelbaar door 3, want de rest is 1. Het blijkt dat G niet deelbaar is door alle priemgetallen 2 t/m P, want de rest bij deling is steeds 1.
Nu kunnen we twee conclusies trekken:
- G is zelf een priemgetal;
- Er moet nog een ander priemgetal zijn dat we niet in het rijtje 2 t/m P hadden staan.
In beide gevallen moeten we concluderen dat we niet alle priemgetallen hebben genoteerd.
En dus hebben we hier een tegenstrijdigheid en dus zijn er oneindig veel priemgetallen.
De wortel uit 2 is irrationaal
Nog een klassieker, wederom uit het ongerijmde.
√2 is irrationaal.
Eerst maar even de betekenis van het woord irrationaal.
De officiële definitie is: Een irrationaal getal is een getal dat niet rationaal is.
En hier komen we niet veel verder mee…
Wat is dan een rationaal getal?
Welnu, een rationaal getal is een getal dat je kunt schrijven als een breuk a/b waarbij a en b gehele getallen zijn en de breuk a/b niet te vereenvoudigen is.
Dat laatste komt neer op het volgende. Wanneer a/b niet te vereenvoudigen is betekent dit dat de ggd(a, b) (lees: De grootste gemene deler van a en b) gelijk is aan 1.
De ggd van twee getallen is de grootste gezamenlijke deler van beide getallen.
Voorbeeld: ggd(12, 24)=? De delers van 12 zijn: 1, 2, 3, 4, 6 en 12. De delers van 24 zijn: 1, 2, 3, 4, 6, 8, 12 en 24. De grootste van beide rijen delers is 12. Dus de ggd(12, 24) = 12.
Het bewijs bestaat uit twee delen, beide uit het ongerijmde.
Het eerste deel noemen we een lemma, omdat dit te eenvoudig is (te voor de hand liggend) om een stelling genoemd te worden.
Lemma: Als a x b deelbaar is door 2 dan is a deelbaar door 2 of b deelbaar door 2 (of allebei). De wiskundige “of” betekent: Of de één of de ander of allebei.
In wiskundige notatie: Als 2|ab, dan 2|a v 2|b. Het teken “|” betekent dus: “deler van”.
Bewijs: Stel 2|ab dan 2∤a èn 2∤b (∤ betekent: geen deler van).
Dus kan ik a schrijven als a=2v+1 en b als b=2w+1, waarbij a en b gehele getallen zijn. Ieder geheel getal keer 2 is even en omdat we er daarna 1 bij optellen zijn a en b dus oneven en is 2∤a èn 2∤b.
Maar nu is ab = (2v+1)(2w+1) = 4vw+2v+2w+1 = 2(2vw+v+w)+1. En omdat zowel v als w gehele getallen zijn en de het product van twee gehele getallen ook een geheel getal is en omdat de som van gehele getallen ook een geheel getal oplevert, is datgene dat tussen haakjes staat dus ook een geheel getal, laten we zeggen q.
Maar nu is ab = 2q+1, waarvan we eerder hebben gezien dat dat een oneven getal is.
En dat is in tegenspraak met het gestelde.
Dus hiermee hebben we het lemma bewezen.
Gevolg: Als 2|a2, dan 2|a (logisch toch?).
Stelling: √2 is irrationaal.
Bewijs: Stel √2 is rationaal. Dan kan ik √2 schrijven als een niet te vereenvoudigen breuk a/b (met dus de ggd(a, b)=1).
Welnu: √2=a/b, dan 2=a2/b2 en dus a2=2b2. Maar dat betekent dat a2 een even getal is, en volgens het gevolg van het lemma hierboven is a dan ook een even getal.
We kunnen a dus schrijven als a=2v, met v een geheel getal.
Maar nu is 2b2=4v2 en dus b2=2v2 en dus wederom volgens het gevolg van het lemma is b dus ook een even getal.
Maar nu is de ggd(a, b) minimaal 2! Want zowel a als b hebben 2 als deler. En dat is in tegenspraal met de eis dat de ggd(a, b)=1, ofwel de breuk a/b is wel te vereenvoudigen.
De conclusie moet dus luiden: √2 is irrationaal.
Een non-bewijs
Dit is een type bewijs dat we nog niet eerder zijn tegengekomen. Bij een non-bewijs wordt een stelling bewezen die niet waar is!
Stelling: 2=3.
Bewijs:
- Stel a=b, dan:
- 2a+3b=3a+2b;
- 3b-3a=2b-2a;
- 3(b-a)=2(b-a), beide zijden delen door (b-a);
- 3(b-a)/(b-a)=2(b-a)/(b-a);
- 3=2 ofwel 2=3.
Ziet u in welke stap het fout gaat? En waarom?
Antwoord Omdat a=b is a-b=0. In stap 5 wordt er gedeeld door (a-b) en dat is dus delen door 0. En dat mag nu eenmaal niet, waarvan hier weer eens een goed voorbeeld waarom! Overigens is het zo dat wanneer een stelling juist is dit volgens strenge wiskundige regels bewezen moet worden. Is een stelling daarentegen niet waar, dan volstaat één tegenvoorbeeld. En nu tot slot: Eerst moeten we bepalen wat we onder “bijzonder” verstaan. Laten we zeggen: Een getal is bijzonder wanneer je daarbij een bepaalde eigenschap kunt bedenken dat niet voor ieder getal geldt. We hebben het hier over positieve gehele getallen, ook wel natuurlijke getallen genoemd waarbij 0 mag meedoen. Wat voorbeelden: 0 is rekenkundig het hoogste getal omdat geen enkel getal door 0 gedeeld kan worden; Je ziet dat je voor elk getal iets bijzonders kunt bedenken. Maar nu het bewijs: Stel dat niet ieder getal bijzonder is. Dan is er dus een eerste (kleinste) niet-bijzondere getal. Maar het feit dat dit dan het eerste niet-bijzondere getal is maakt dat getal natuurlijk weer bijzonder. Conclusie: Elk getal is bijzonder. En van dit bewijs mag u denken wat u wilt …Elk getal is bijzonder
1 is rekenkundig het laagste getal omdat ieder getal door 1 gedeeld kan worden;
2 is het eerste en tevens enige even priemgetal;
3 is het eerste oneven priemgetal;
4 is het eerste samengestelde getal, alsook het eerste echte kwadraat;
5 is het aantal vingers aan één hand (behalve bij Tineke de Nooij);
6 is het eerste volmaakte getal (te schrijven als de som van de echte delers);
.
.
.
26 is het enige getal dat ligt tussen een kwadraat en een derde macht;
.
.
.
97 is het grootste priemgetal onder de 100;
.
.
.
144 is een Filtz-getal
145 is een Gelderman-getal
.
.
.