Inhoud Deze aflevering gaat over één van de bekendste rijen getallen, die van Fibonacci en waar we dit allemaal kunnen tegenkomen. We gaan ook kijken naar variaties op de rij en een paar abstracties. Maar we beginnen bij het begin. De rij van Fibonacci ziet er als volgt uit: (0), 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … Je kunt deze gemakkelijk voortzetten, want het volgende element is de som van de voorgaande twee elementen. Je begint de rij met de getallen 1 en 1. In wiskundige notatie ziet de rij er als volgt uit: Merk op dat wanneer we de index n vanaf 0 laten lopen we deze notatie krijgen: Maar dit levert exact dezelfde rij op. De eerste die deze rij beroemd heeft gemaakt is Leonardo van Pisa, bijgenaamd Fibonacci. In zijn werk “Liber Abaci” (het boek over rekenen) geeft hij de volgende uitleg over de rij: Begin met één paar konijnen (een mannetje en een vrouwtje). In de derde maand zijn ze geslachtsrijp en produceren dan 1 paar nieuwe konijnen (mannetje en vrouwtje) per maand. We tellen nu per maand het aantal paren konijnen. In maand 1 hebben we (dus) 1 paar. En deze rij groeit dus gestaag. Het blijkt dat Fibonacci getallen veel in de natuur voorkomen. Zo zijn het aantal blaadjes aan een bloem vaak een Fibonacci getal: De dennenappel en de zonnebloem hebben spiralen; het aantal spiralen , zowel linksom als rechtsom, zijn vaak weer Fibonacci getallen. Maar ook in ons eigen lichaam zijn ze te vinden: Zo hebben we 1 hart en 1 hoofd, 2 armen, 2 benen, 2 ogen en 2 oren, 3 botten in elke arm en been, 5 vingers aan elke hand en 5 tenen aan elke voet. De torso heeft 5 “aanhangsels”: Twee armen, twee benen en een hoofd. Het voorbeeld over de konijnen was door Fibonacci gebruikt om een eenvoudige duiding aan de rij te geven. In de bijenwereld is de rij echter goed terug te vinden. En wel in de stamboom van een bijenfamilie. De onderste generatie bestaat uit 2 bijen, die daarboven uit 3, daarboven 5 en de bovenste bestaat uit 8 bijen (etc.). Laten we eens kijken naar de opeenvolgende fracties van fn+1/fn, we delen dus steeds twee opeenvolgende Fibonacci-getallen op elkaar: Het lijkt erop dat deze fractie naar een limiet gaat en dat is ook zo! De limiet is de gulden ratio, ook wel gulden snede, gouden ratio of gouden snede genoemd. Hoe komen we aan deze limiet? Bekijk onderstaande afbeelding: We zien een lijnstuk met een lengte van a+b. De gulden snede is nu de verhouding van a:b tot (a+b):a. En dit levert een vergelijking op: Nemen we b=1 (dat mag omdat het hier om een verhouding gaat) dan krijgen we: En als we deze vergelijking oplossen dan krijgen we: En de tweede oplossing is ongeveer 1,618033…, de gulden ratio. En omdat dit een “speciaal” getal is geven wiskundige daar graag een letter aan en voor de gulden snede is dat de Griekse letter Φ (hoofdletter phi) of φ (kleine letter phi). Waarom wordt φ nu de gulden snede genoemd? Bovenal omdat wij mensen dit een mooie verhouding vinden. Je vindt de gulden snede heel veel terug in het perspectief van kunst. Maar ook in de symmetrie van de mens, bijvoorbeeld de plaats van de pols ten opzichte van de lengte vanaf de ellenboog tot en met de hand. En zo verder. Nog een voorbeeld: De gulden spiraal: Je kunt deze spiraal in gedraaide, gespiegelde, in- of uitgerekte vorm vaak leggen op verschillende kunst zodat het perspectief duidelijk wordt. Maar wat heeft deze spiraal nog van doen met de rij van Fibonacci? Kijk maar eens hoe deze is opgebouwd: De spiraal kromt zich een weg vanuit het midden naar buiten toe door de verschillende vierkanten. Maar kijk nu eens goed naar de lengte van de zijden van de vierkanten: 1, 1, 2, 3, 5, 8, … Precies de getallen uit de rij van Fibonacci. Een vraag die zich wellicht opdoemt is: Is er een betekenis voor de eerste oplossing van voornoemde vergelijking en zo ja welke? Deze vraag gaan we in de volgende paragraaf behandelen. Laten we de rij eens uitbreiden naar de negatieve kant, ofwel hoe ziet de rij eruit voor negatieve n. We beginnen weer met F1=F2=1. F0 is nu het verschil van F2 en F1 ofwel F0=F2-F1=1-1=0. F-1 is dan F1-F0=1-0=1 We zien een merkwaardig patroon opdoemen: De getallen zijn afwisselend positief en negatief. Laten we weer eens kijken naar de fracties van Fn+1/Fn: Ook hier zien we een limiet ontstaan van -1,618034… En dit is de eerste oplossing van a2-a-1=0 ofwel: Afspraak: Voor de rest van rest van dit artikel gebruiken we de kleine letter phi voor de eerste (negatieve) oplossing voor bovenstaande vergelijking en de hoofdletter phi voor de tweede (positieve) oplossing voor bovenstaande vergelijking. Dus: Welke grafiek krijgen we nu als we de getallen van de uitgebreide rij van Fibonacci met elkaar verbinden? Welnu, deze: Voor negatieve waarde van n zig-zagt de grafiek en voor positieve waarde stijgt de grafiek. De volgende vraag die we gaan beantwoorden is: Bestaat er een formule die de getallen van Fibonacci voortbrengt? En ja, deze bestaat! Merk op dat: Tevens geldt (maar minder belangrijk voor dit verhaal): De formule van Binet luidt als volgt: En zo levert bijvoorbeeld B(3)=2 op en B(7)=13 en B(0)=0 en B(-4)=-3 etc. Wat een prachtige formule. Maar wat zou er nu gebeuren als we deze formule eens gaan beschouwen met reële getallen in plaats van gehele getallen? Kortom: wat is dan bijvoorbeeld B(1,5), of B(-π)? We lopen echter wel meteen tegen een probleem aan. Op school hebben we geleerd dat machtsverheffen herhaald vermenigvuldigen is. Dus xn=x.x.x. … x., en dat n keer. Verder hebben we geleerd dat x0=1. En tot slot de volgende twee regels: Om kort te gaan moet de exponent (n) uit de verzameling ℕ∪{0}, de verzameling van de gehele getallen met nul, komen. Willen we de exponent toch uit ℝ laten komen dan krijgen we antwoorden uit de Binet formule die zogenaamd complex zijn, ofwel uit de verzameling ℂ komen (zie ook het artikel Formule van Euler). Wanneer we een en ander in Excel willen doen dan lukt dat niet voor de reële getallen. De beperkt aantal complexe functies in Excel is niet toereikend. Zo is B(1,5)≈0.920442065259926+0.21728689675164012i en We gaan eerst eens kijken naar: ofwel naar de positieve reële getallen met 0. De grafiek van de “positieve” kant van Binet ziet er als volgt uit: Een mooie rustige kringelende grafiek. Merk op dat punt 1 twee maal wordt doorkruist. Precies wat je zou verwachten, niet waar? Maar hoe ziet de “negatieve” kant van de grafiek er nu uit? De (laatste) grafiek uit de vorige paragraaf doet vermoeden dat er iets van een zaagtand uitkomt. Maar niets is minder waar: Er komt een prachtige spiraal uit die keurig krult tussen de afwisselende positieve en negatieve Fibonacci getallen bij een negatieve index. En beide grafieken gecombineerd ziet er als volgt uit: De rij van Lucas (vernoemd naar de 19e-eeuwse Fransman François Lucas) volgt dezelfde regel als de rij van Fibonacci maar begint de rij met 2, 1 (in plaats van 0, 1). Let op: De 2 is dus de 0e positie. Het blijkt dat wanneer de natuur afwijkt van een Fibonacci getal het dan wel vaak een Lucas getal is. De rij begint als volgt: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, … Gaan de fracties van de opeenvolgende getallen weer naar een limiet toe? Het antwoord is jawel en dat is dezelfde limiet als bij de Fibonacci getallen, namelijk de gulden snede Φ. En als we de Lucas rij in negatieve richting uitbreiden dan zien we (beginnend met index 0 en daarna aflopend): 2, -1, 3, -4, 7, -11, 18, -29, 47, -76, … En de fracties van opeenvolgende getallen (aan de negatieve kant) is inderdaad φ. Is dit nu toeval? Nee, dat is het niet. Laten we eens kijken naar het voorschrift. Die zijn voor beide rijen (Fibonacci en Lucas) hetzelfde: Rn = Rn-1 + Rn-1. De fracties de we vervolgens bekijken ook: Rn+1 / Rn. Eén en ander substitueren levert op: Rn+1 / Rn = Rn+1 / (Rn-1+Rn-2) => Rn+1(Rn-1+Rn-2)=Rn.Rn+1 => Rn=Rn-1+Rn-2, wat natuurlijk het voorschrift is! Het voorschrift Rn = Rn-1 + Rn-1 leidt tot de zogenaamde karakteristieke vergelijking r2-r-1=0. En die vergelijking zijn we al eerder tegengekomen en de uitkomsten daarvan zijn bekend, nl.: r=φ of r=Φ. Het maakt dus niet uit welke startwaarden er worden genomen, de fracties zullen altijd leiden naar φ (bij negatieve index) of naar Φ (bij positieve index). Verder gelden er nog allerlei verbanden tussen de rijen (n≥0): Ln=Fn-1+Fn+1 Bestaat er voor de rij van Lucas ook iets als een formule van Binet? Het antwoord is jawel. Sterker nog: Voor iedere twee beginwaardes bestaat er een Binet formule. Uit het voorschrift Fn=Fn-1+Fn-2 volgt de karakteristieke vergelijking r2-r-1=0, zoals we hierboven al gezien hebben, met oplossingen r=φ of r=Φ. Hieruit volgt de generieke vergelijking (zonder dat ik hier de achterliggende wiskunde verklaar): Als an=an-1+an-2 dan an=αr1n+βr2n. Hierboven hebben we r1 en r2 al uitgerekend, dus krijgen we: We krijgen dus een stelsel van 2 vergelijkingen met 2 onbekenden: En dit stelsel is oplosbaar. Oplossing We lossen dit op door middel van matrices. Vooraf merk op dat: Φ – φ = √5 Verder vanaf de laatste: In de verschillende stappen werken we naar de eenheidsmatrix toe. De laatste matrix is de eenheidsmatrix en levert onze waarde voor α en β op. De oplossingen zijn: α = 1 en β = 1. De Binet formule voor Lucas luidt nu als volgt: In deze paragraaf gaan we kijken naar de Fibonacci getallen modulus een bepaald getal. Modulus rekenen is niets anders dan klokrekenen. En klokrekenen kunnen we natuurlijk allemaal. Kijk maar: Het is nu tien over negen (9:10). Hoe laat is het over 55 minuten? Niemand zal zeggen 65 over negen (9:65), maar vijf over tien (10:05). We kijken eerst naar de hele uren, gaat de tijd daar over heen, zoals in het voorbeeld, dan kijken we vervolgens hoeveel (minuten) er nog over zijn en tellen die weer bij het hele uur op. En dat is precies wat het is. Bij modulo rekenen kijken we naar de rest die over blijft bij een deling. Een paar voorbeeldjes: Wat is 7 mod 4? Dit betekent: Wat is de rest wanneer je 7 door 4 deelt. Welnu: 4 kan (geheel) 1 keer in 7; en dan blijft er 3 over. En zo is 7 ≡ 1 (mod 3), want 3 past 2 keer (geheel) in 7 en dan blijft er 1 over. Merk op: Bij klokrekenen kan de rest nooit groter zijn dan de deler. En dat gaan we nu eens toepassen op de Fibonacci getallen. Laten we eerst eens kijken naar Fib mod 4, ofwel wat zijn de “resten” als we de Fibonacci getallen delen door 4: De resten zijn inderdaad allemaal kleiner dan 4. Verder zien we dat de sequentie van resten zich herhalen na 6 Fibonacci getallen: 0, 1, 1, 2, 3, 1 en dat patroon wordt daarna herhaald. Laten we eens kijken naar Fib mod 2: Dan herhaalt de rest sequentie zich al na 3 keer: 0, 1, 1. En tot slot kijken we hier naar Fib mod 3: Hoewel we hier te weinig data hebben om de herhaling te zien vertel ik dat de rest sequentie hier 8 is. Wanneer we naar de tabellen kijken dat kan het opvallen dat iedere sequentie begint met 0, 1, en dat is ook zo. Dus in de laatste tabel zien we dat 0, 1 weer terug komt vanaf n=8, dus is de rest sequentie 8 (n begint bij 0). De lengte van de rest sequentie noemen we het Pisano getal (uiteraard weer vernoemd naar Leonardo van Pisa). Hieronder een tabelletje met wat Pisano getallen: Wat misschien nog niet is opgevallen is dat de resten ook de Fibonacci regel volgt alleen steeds gecorrigeerd met de modulus. Kijk maar eens naar de eerste tabel (mod 4): De resten zijn: Na al deze getalletjes weer eens wat plaatjes. Met bovenstaande kunnen we leuke afbeeldingen maken. We gaan eerst wat cirkels met lijnen maken en wel als volgt: Teken een cirkel. Zet op de cirkel op even grote afstand van elkaar het aantal stippen van de modulus. Trek vervolgens lijnen tussen de stippen volgens de resten. We krijgen dan deze figuur: Laten we nog eens wat cirkeltjes bekijken: Onder de cirkels staat ook nog het aantal nullen dat in de rest sequentie voorkomt. Het blijkt dat er altijd 1, 2 of 4 nullen zijn. Verder valt op dat wanneer het aantal nullen 1 is de figuur asymmetrisch is (behalve bij mod 2), als het aantal nullen 4 is de figuur symmetrisch is en bij 2 nullen beide varianten voorkomen. We kunnen met die resten ook nog andere plaatjes maken. Ook dan krijg je hele spannende plaatjes. Opvallend: Als we beginnen met mod 1, dan krijg je dus gewoon de Fibonacci getallen dan krijg je dit figuur: Een grote plus; hoe toepasselijk. Een paar andere voorbeelden: Een aantal figuren keert terug. Sommige figuren zijn keurig symmetrisch terwijl andere “wild” tekeer gaan. Ze hebben wel allemaal wat fractalachtigs. De bijschriften vertellen welke modulus gebruikt is, hoe vaak een rest-sequentie gebruikt is en onder welke hoek er is gedraaid. Bij het wijzigen van de hoek ontstaan ook spannende plaatjes (hier wat variaties op mod 9): We weten dat Φ ≈ 1,618033989… . Laten we eens kijken naar Φ2. Op de rekenmachine levert dit op: Φ2 ≈ 2,618033989… . Als we goed naar al deze uitkomsten kijken dan lijkt het erop dat: 1/Φ = Φ – 1 en Φ2 = Φ + 1. Dat zou een opmerkelijk resultaat zijn. Laten we eens kijken of er inderdaad een getal bestaat waarvan het kwadraat het getal vermeerderd met 1 oplevert. We noemen dat getal maar even x (origineel, niet waar?). Dus x2=x+1 ofwel x2-x-1=0. Maar die zijn we, inderdaad, al eerder tegengekomen. En de uitkomst was dat x=φ of x=Φ. En als we kijken naar de reciproke, dan krijgen we: De opmerkelijke resultaten van hierboven zijn dus juist. Tevens is Φ het enige getal met deze eigenschappen. Overigens is het natuurlijk altijd mogelijk om een getal te vinden waarvan het kwadraat gelijk is aan het getal zelf plus een bepaalde constante omdat de vergelijking x2-x-c=0 nu eenmaal altijd een oplossing heeft, ook al is deze wellicht complex. Maar dan is de reciproke niet gelijk aan dat getal minus 1. Maar het wordt nog veel leuker! Wat zou Φ3 zijn? We weten dat Φ2 = Φ+1. Welnu: Φ3 = Φ.Φ2 = Φ(Φ+1) = Φ2+Φ = (Φ+1)+Φ = 2Φ+1. Laten we eens kijken naar wat meer (opeenvolgende) machten: Φ4 = Φ.Φ3 = Φ(2Φ+1) = 2Φ2+Φ = 2(Φ+1)+Φ = 3Φ+2. Er ontvouwt zich een patroon. Als we bovenstaande opeenvolgende machten doorzetten dan blijkt inderdaad: Φ7 = … = 13Φ + 8 Ziet u in de resultaten van de verschillende machten de Fibonacci getallen ook terugkomen? Er geldt dus de volgende opmerkelijke regel: Φn = FnΦ+Fn-1, voor n≥0. Voor n<0 geldt: φn=-Fnφ-Fn+1. Hoe mooi! Met al het bovenstaande kunnen we nu wat nader ingaan op beide bekende rijen. We kijken nog even naar de rij van Lucas: Vanaf index 2 wordt het interessant. Het lijkt erop dat [Φn] gelijk is aan Ln, en dat is ook zo! Dus: ∀ n∈ℕ, n>1 geldt: Ln = [Φn]. We weten ook dat Fn =FnΦ + Fn-1. En volgens de definitie is Fn = Fn-1 + Fn-2. Merk op dat Fn = Φ.Fn-1; zo zijn we immers aan Φ gekomen. Om niet in de war te geraken met indexen gaan we uit van onderstaande tabel: De onderste regel (L/F) komt zo aan de orde. We gaan nu de bovenstaande formules combineren. Ln = [Φn] =FnΦ + Fn-1 = Fn+1 + Fn-1. Dus Ln = Fn-1 + Fn+1. En dit is toch een aardig verband tussen Fibonacci en Lucas. Kijken we tot slot nog even naar de verhouding tussen Lucas en Fibonacci. De onderste regel van bovenstaande tabel geeft Ln / Fn aan. De vraag is of deze verhouding naar een limiet gaat. En dat is zo. De limiet van L/F is √5. Hoe fraai. En zo kunnen we nog een formule maken: We kunnen de Fibonacci getallen ook willekeurig genereren door een muntje op te gooien: Je krijgt dan iets dat er als volgt uit kan zien: In de laatste kolom staat weer de factor van twee voorgaande getallen. Daar is veel aan gerekend. Opmerkelijk is dat deze factor ook een limiet heeft, namelijk: 1,1319882487943…, het getal van Visnath. Het duurt echter heel lang voordat deze limiet wordt bereikt. Met de rij van Fibonacci kun je ook getallen raden. Kijk maar eens op deze pagina (opent in een nieuwe tab). Benieuwd hoe dit gaat? Of heeft u het al in de gaten? Oplossing Maak 7 kaarten als volgt: Het eerste getal van iedere kaart is een Fibonacci getal. Dit heeft te maken met het feit dat je ieder natuurlijk getal kunt schrijven als een som van Fibonacci getallen. Begin je bij de Fibonacci rij met twee vaste waarden, bij een Tribonacci rij begin je met drie vaste waarden. De regel daarna is dat de volgende term de som van voorgaande drie termen is. Beginnen we de rij met 1, 1, 1 dan is de 4e term 1+1+1=3. En ook de fracties Tn/Tn-1 gaan weer naar een limiet die gegeven wordt door de oplossing van de vergelijking x3-x2-x-1=0. Deze limiet is (ongeveer) 1,839287. Berekening Voor het oplossen van een derdegraads vergelijking bestaan meerdere methodes. We gaan uit van de standaard vorm: ax3+bx2+cx+d=0. Een oplossing krijg je door de volgende (abcd-) formule: De voorwaarde voor bovenstaande formule is dat a (de factor voor x3) gelijk aan 1 is. Wanneer dat niet het geval is deel je alle factoren eerst door a. We zoeken hier een oplossing voor de vergelijking x3-x2-x-1=0, dus En dan is het een invuloefening geworden waaruit blijkt dat x ≈ 1,839287. De andere twee oplossingen vind je nu door de vergelijking te delen door (x-1,839287). Je houdt dan een tweedegraads vergelijking over en die is op te lossen met de gewone abc-formule. Een Fibonacci gedicht is een gedicht dat uit een aantal regels bestaat. Het aantal woorden per regel is een (oplopend) Fibonacci getal, dus regel 1 en regel 2 bestaan uit 1 woord, regel 3 bestaat uit 2 woorden etc. Een mooi (Engels) voorbeeld: I Ook in de bekende driehoek van Pascal zitten de Fibonacci getallen. De driehoek van Pascal wordt als volgt opgebouwd: Begin bovenaan met een 1, Je krijgt dan: De bovenste regel heeft index 0. De getallen op de (horizontale) regels zijn de coëfficiënten van (x+y)n. Bijvoorbeeld: (x+y)2=x2+2xy+y2, en (x+y)3=x3+3x2y+3xy2+y3. En nu de driehoek met de Fibonacci getallen (gekleurd): Werkend van boven naar onder en van links naar rechts; kleur het witte vierkantje, ga 1 naar onder en 3 naar rechts, geeft het vierkantje dezelfde kleur. Herhaal totdat de driehoek verlaten is. Tel de getallen van de gekleurde vierkantjes bij elkaar op. Als n een deler van m is dan is Fn een deler van Fm. En omgekeerd gaat ook op, dus: Het laatste cijfer van Fn ≡ Fn mod 10 als n<100. De notatie voor Pisano getallen is π(n). Met de mediant wordt een “foutieve” optelling van breuken bedoeld, namelijk tellers optellen en noemers optellen. Het symbool is ⊕. Kijk nu eens naar de volgende serie breuken: Dit levert de volgende rij breuken op: Zie je de Fibonacci getallen terug komen in zowel de tellers als de noemers? Wanneer je een willekeurig Fibonacci getal optelt bij het Fibonacci getal dat 4 plaatsen verderop staat en deze som deelt door het Fibonacci getal dat 2 plaatsen verderop staat is dit quotiënt altijd deelbaar door 3. Dus 3|(Fn+Fn+4)/Fn+2. Bewijs Noem willekeurig Fibonacci getal a. Zie het artikel daarover. Er is een regel waarmee je kunt bepalen of een willekeurig geheel getal een Fibonacci getal is, ofwel of de voorkomt in de (standaard) rij van Fibonacci; de regel staat bekend onder de naam: De regel van Ira Gessel. Neem een willekeurig getal q. Voorbeelden: Neem q=144, dan is √(5*1442+4) = 322 geheel en dus is 144 een Fibonacci getal. De GGD(Fn, Fm) = FGGD(n, m), met F1 = F2 = 1. De GGD(Fn, Fn+1) = 1 ofwel Fn en Fn+1 zijn altijd co-priem. Kijk eens naar de volgende som: 0.0 Bij iedere stap komt er één decimaal bij. De cijfers die erbij komen volgen de rij van Fibonacci . De som is precies 1/89. Leonardo van Pisa is omstreeks 1170 in Pisa geboren en circa 1250 overleden. De bijnaam Fibonacci betekent de zoon van Bonaccio, de bijnaam van zijn vader dat “goedzak” betekent. Een andere, oude, naam voor Pisa is Pisano. Leonardo was een wiskundige die tijdens zijn studie vele reizen maakten waaronder naar het oosten. Daar kwam hij in aanraking met de Indische manier van rekenen en de Arabisch-Indische cijfernotatie. François Lucas is op 4 April 1842 geboren in Amiens en is op 3 Oktober 1891 gestorven. Hij was een wiskundige. Buiten het feit dat hij zich bezig hield met serieuze wiskunde, waaronder onderzoek naar Diofantische vergelijkingen, en primaliteiten was hij ook recreatief wiskundige. De bekende Torens van Hanoi komen uit zijn koker. Jacques Binet is geboren on Rennes op 2 Februari 1786 en in Parijs gestorven op 12 Mei 1856. Hij was een wiskundige en astronoom. Hij hield zich, onder andere, bezig met de matrixtheorie waar hij de regel voor matrixvermenigvuldigingen vaststelde. En natuurlijk is hij bekend van de formule van Binet, waarvan gezegd moet worden dat deze al een eeuw eerder was gepubliceerd door de Moivre. Blaise Pascal is geboren op 19 Juni 1623 in Clermont-Ferrand en gestorven op 19 Augustus 1662 in Parijs. Hij was (heeft u even?) een wiskundige, natuurkundige, filosoof, en ingenieur. Verder hield hij zich actief bezig met de Christelijk leer. Hij is bovenal bekend door zijn baanbrekende werk op het gebied van de kansrekening. Maar ook onderscheidde hij zich op het gebied van de integraalleer, projectieve meetkunde, hydrostatica, hydrodynamica en combinatoriek. In dat laatste vakgebied ontstond de driehoek van Pascal. Hij bouwde ook de eerste mechanische rekenmachine, de Pascaline, die kon optellen en aftrekken. En “last but not least” is er natuurlijk de Wet van Pascal: De druk die op een vloeistof wordt uitgeoefend plant zich in alle richtingen met dezelfde grootte voort. De volgende programma’s heb ik gebruikt: Code Excel functies (VBA) Function BinetInt(ByVal n As Integer) As Double w5 = 5 ^ 0.5 Function BinetLucasInt(ByVal n As Integer) As Double w5 = 5 ^ 0.5 Function MyMod(ByVal a As Double, ByVal b As Double) As Double mm = a – (b * Int(a / b)) Function Pisano(ByVal m As Long) As Long If m > 2 Then Binet grafieken (Python) Pisano figuren (Q&D; kan/moet verbeterd worden) (Python) Getal raden (PHP) <?php <html> <?php include ‘functions.php’; ?> <?php $kaart1 = array(1, 4, 6, 9, 14, 17, 19, 22, 25, 27, 30); function ToonKaart($nr) if ($nr == 1) function Speel() if (isset($_GET[‘beurt’])) <body> Bijen: https://yoo.rs/wetenschap-wiskunde-in-de-natuur-fibonacci-reeks-1630249277.html Youtube Pisano: https://www.youtube.com/watch?v=Nu-lW-Ifyec&t=4s&ab_channel=Numberphile Inleiding
Een simpele rij getallen die op de meest opmerkelijke plekken opduikt. Zo vinden we deze getallen in de natuur, in de kunst, in het menselijk lichaam. Maar ook meer abstract. Zo vind ik het opmerkelijk dat een formule met irrationale getallen de rij kan voortbrengen. En dat deze formule een opmerkelijke grafiek voortbrengt.
De getallen vormen ook de basis voor de zogenaamde gulden snede en zijn terug te vinden in de driehoek van Pascal.De rij van Fibonacci
Dat ik de nul tussen haakjes heb staan is om aan te geven dat het 0de element 0 is.
In maand 2 hebben we nog steeds 1 paar.
In maand 3 komt er 1 paar konijnen bij omdat het eerste paar heeft geproduceerd, dus er zijn nu 2 paar.
In maand 4 komt er weer een paar bij omdat het eerste paar weer heeft geproduceerd, dus een totaal van 3 paar.
In maand 5 komen er 2 paar bij, 1 paar van het eerste paar maar nu ook van het tweede paar omdat deze nu ook geslachtsrijp zijn, een totaal van 5 paar.
En zo voort… (het is bij de konijnen af!)Fibonacci en de natuur

We hebben 5 zintuigen: Zien, horen, voelen, ruiken en proeven.
Maar ook in ons diepste wezen: Een DNA-streng is 34 ångström lang en 21 ångström breed; 1 ångström = 10-10m ofwel 0,1 nanometer (1 miljardste meter) of 100 picometer (1 biljoenste meter) en wordt gebruikt om de grootte van een atoom aan te geven (0,5Å<atoom<6Å).
Een bij kan ontstaan uit een bevrucht of onbevrucht eitje. Uit een onbevrucht eitje komt een dar (een mannetje) en uit een bevrucht eitje komt een werkster (vrouwtje). Dit betekent dus dat een Dar slechts 1 ouder heeft (een moeder) en een werkster 2 ouders (vader en moeder).
Beginnen we nu met één werkster (W) en één dar (D) dan zien de eerste 4 generaties van hun stamboom er als volgt uit: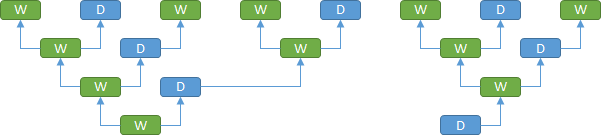
De gulden ratio
n
Fibn
Fibn+1/Fibn
1
1
2
1
1
3
2
2
4
3
1,5
5
5
1,666666667
6
8
1,6
7
13
1,625
8
21
1,615384615
9
34
1,619047619
10
55
1,617647059
11
89
1,618181818
12
144
1,617977528
13
233
1,618055556
14
377
1,618025751
15
610
1,618037135
16
987
1,618032787
17
1597
1,618034448
18
2584
1,618033813
19
4181
1,618034056
20
6765
1,618033963
![]()

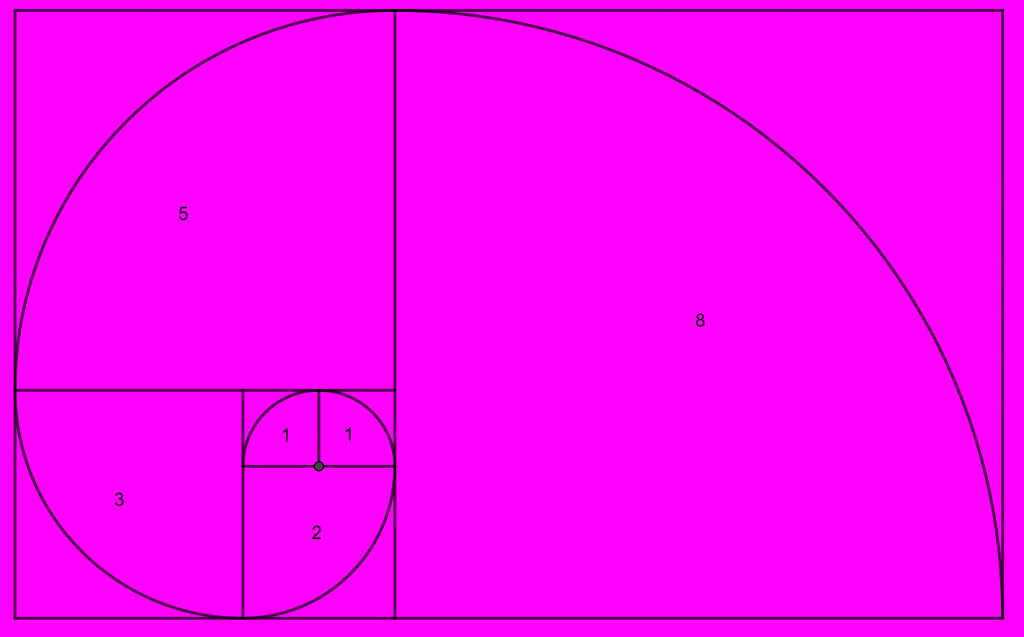
Uitbreiding van de rij
F-2=F0-F-1=0-1=-1
F-3=F-1-F-2=1–1=2
F-4=F-2-F-3=-1-2=-3
n
Fibn
Fibn+1/Fibn
2
1
1
1
1
0
0
0
-1
1
bn
-2
-1
-1
-3
2
-2
-4
-3
-1,5
-5
5
-1,666666667
-6
-8
-1,6
-7
13
-1,625
-8
-21
-1,615384615
-9
34
-1,619047619
-10
-55
-1,617647059
-11
89
-1,618181818
-12
-144
-1,617977528
-13
233
-1,618055556
-14
-377
-1,618025751
-15
610
-1,618037135
-16
-987
-1,618032787
-17
1597
-1,618034448
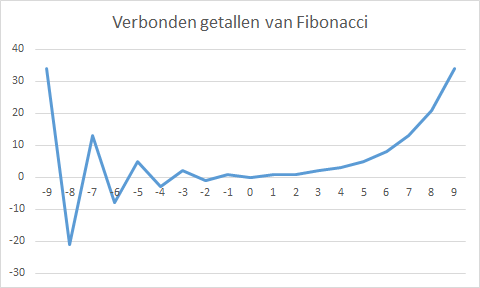
De formule van Binet
Dus maar even Python erbij gepakt.
B(-π)≈1.9292695604395613-0.8726530431453033i.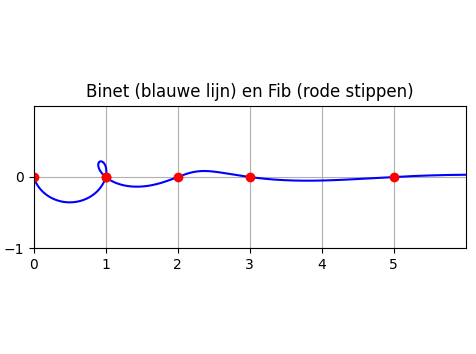
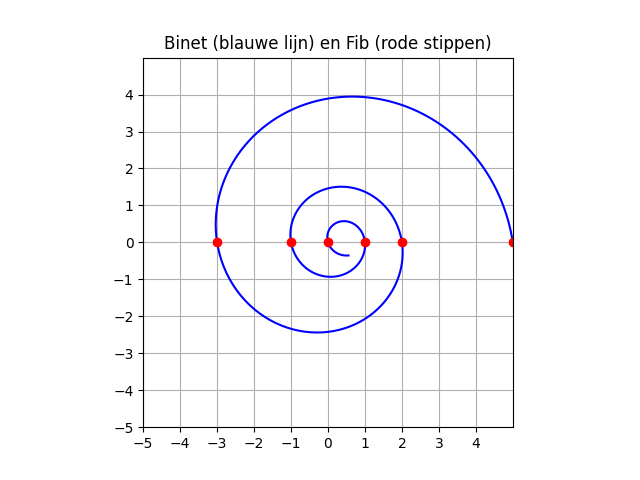
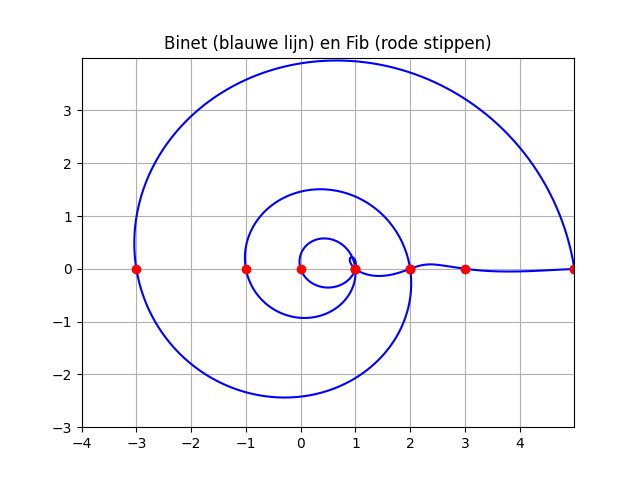
De rij van Lucas
F2n=Ln*Fn
Ln=Fn+2Fn-1
an=αφn+βΦn. Ook weten we wat a0 is en wat a1 is, namelijk a0=2 en a1=1.
φ – Φ = -√5
φ + Φ = 1
en uit bovenstaande volgt:
1 -2φ = φ + Φ – 2φ = Φ – φ = √5 (heb ik later nodig)
Met I worden de elementen van de bovenste regel bedoeld en met II de elementen van de onderste regel, steeds van links naar rechts.
In stap1 haal je dus van II, φ maal de waarde van I af.
In stap2 deel je II door √5 en
in stap 3 haal je II van I af.Klokrekenen
Wat we hier dus eigenlijk doen is rekenen met een klok van 12 uur en 60 minuten.
In wiskundige termen rekenen we hier modulo 12.
Dus 7 mod 4 = 3.
Notatie: 7 mod 4 = 3 of 7 ≡ 3 (mod 4).
Dus a mod b kan nooit groter zijn dan b, sterker nog a mod b is altijd kleiner dan b.
n
fn
fn mod 4
0
0
0
1
1
1
2
1
1
3
2
2
4
3
3
5
5
1
6
8
0
7
13
1
8
21
1
9
34
2
10
55
3
11
89
1
12
144
0
13
233
1
14
377
1
n
fn
fn mod 2
0
0
0
1
1
1
2
1
1
3
2
0
4
3
1
5
5
1
6
8
0
7
13
1
8
21
1
9
34
0
10
55
1
n
fn
fn mod 3
0
0
0
1
1
1
2
1
1
3
2
2
4
3
0
5
5
2
6
8
2
7
13
1
8
21
0
9
34
1
10
55
1
11
89
2
12
144
0
mod
Pisano
2
3
3
8
4
6
5
20
6
24
7
16
8
12
9
24
10
60
11
10
12
24
13
28
14
48
15
40
16
24
0, 1, 1, 2, 3, 1
maar dat is:
0, 1, (0+1) mod 4≡1, (1+1) mod 4≡2, (1+2) mod 4≡3, (2+3) mod 4≡1
De eerste twee resten (0 en 1) zijn de startgetallen en daarna is het weer de som van de voorgaande twee getallen, alleen nu modulo 4.
Dus als we bijvoorbeeld modulo 4 rekenen dan hebben we een cirkel met 4 stippen (0 t/m 3), elk 90° van elkaar verwijderd en trekken we de volgende lijnen: van 0 naar 1, van 1 naar 1, van 1 naar 2, van 2 naar 3 en van 3 naar 1 (want de resten zijn 0, 1, 1, 2, 3, 1).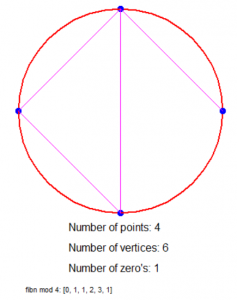
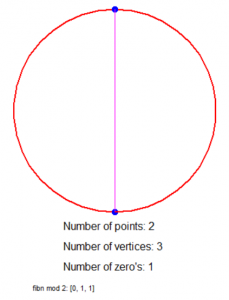
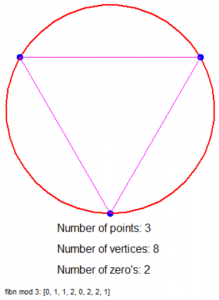

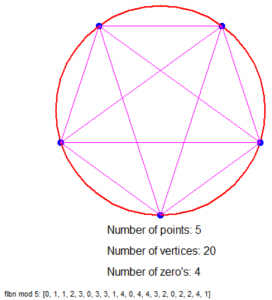
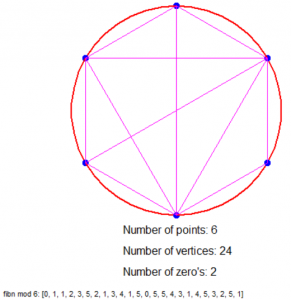
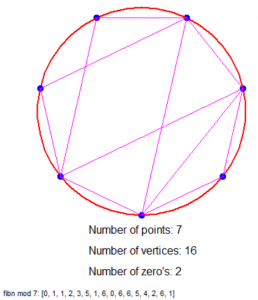
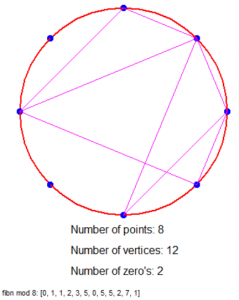
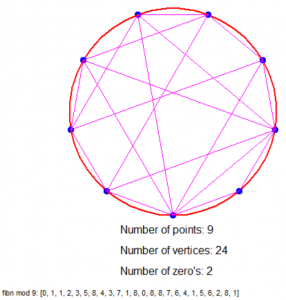
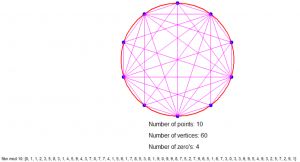
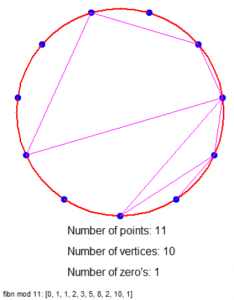
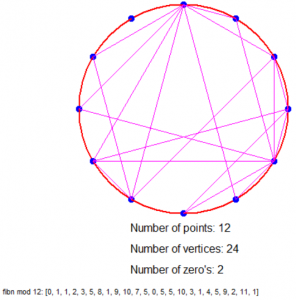
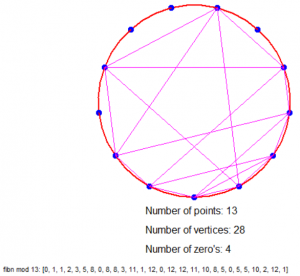
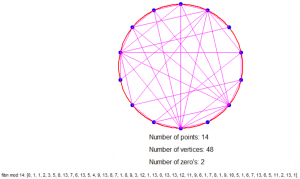
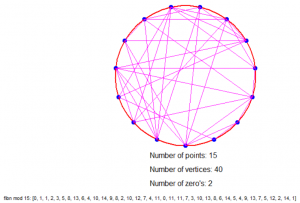
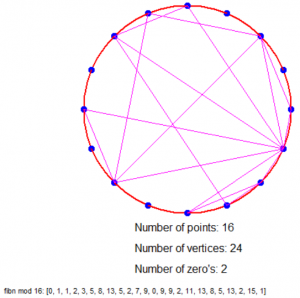
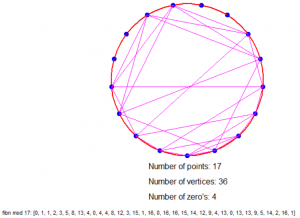
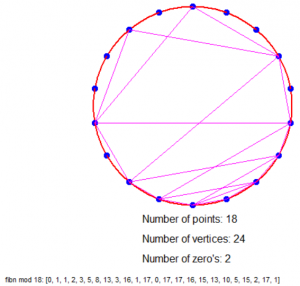
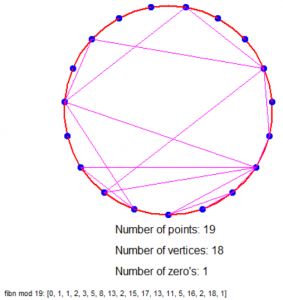
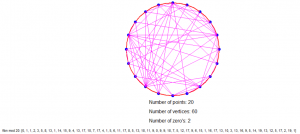
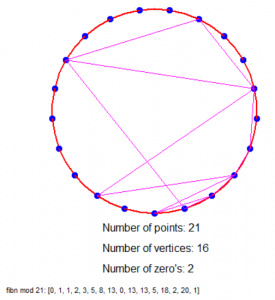
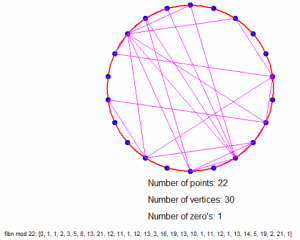
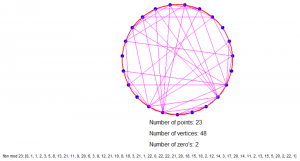
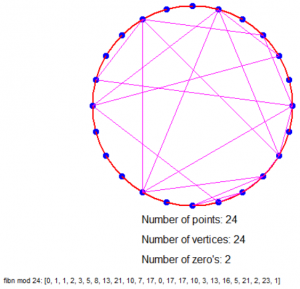
Is dat nu niet geinig?
Laten we de volgende regels afspreken:
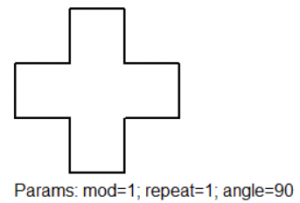

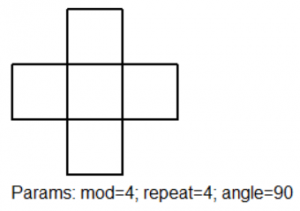
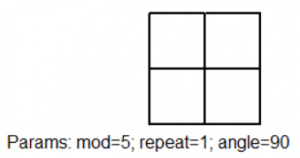
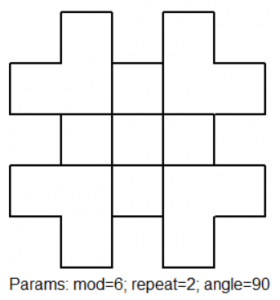
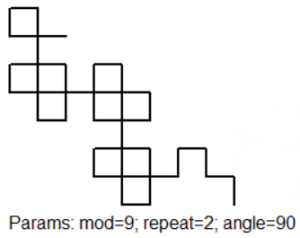
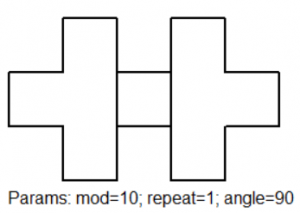
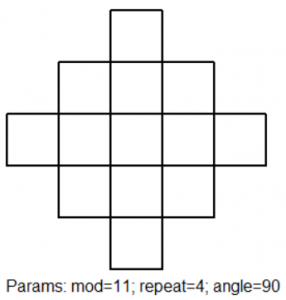
Machtsverheffen
We weten ook dat 1/Φ ≈ 0,618033988… .
1/Φ = Φ – 1 ⇒ (beide zijden met Φ vermenigvuldigen) 1 = Φ2 – Φ ⇒ Φ2 – Φ -1 = 0, en dat is dus hetzelfde als x2-x-1=0.
(We moeten de antwoorden nog wel invullen in de originele vergelijking om er zeker van te zijn dat 1/Φ geen deling door nul oplevert; maar dat doet het niet!)
Dus de derde macht van Φ is 2 keer Φ plus 1.
Φ5 = Φ.Φ4 = Φ(3Φ+2) = 3Φ2+2Φ = 3(Φ+1)+2Φ = 5Φ+3.
Φ6 = Φ.Φ5 = Φ(5Φ+3) = 5Φ2+3Φ = 5(Φ+1)+3Φ = 8Φ+5.
Φ8 = … = 21Φ + 13
…Fibonacci en Lucas
index
Lucasindex
Φindex
0
2
∼
1
1
∼
2
3
2,618…
3
4
4,236
4
7
6,854
5
11
11,090…
De blokhaken ( […] ) betekenen dat de waarde tussen de blokhaken moet worden afgerond naar een geheel getal.
i
0
1
2
3
4
5
6
7
8
L
2
1
3
4
7
11
18
29
47
F
0
1
1
2
3
5
8
13
21
L/F
∼
1
3
2
2.33…
2.2
2.25
2.23…
2.23…
Variaties op een thema
Random Fibonacci
We beginnen weer met 1 en 1.
Daarna gooien we een muntje op:
Valt de munt op “kop” dan tellen we de twee voorgaande getallen bij elkaar op,
valt de munt op “munt” dan trekken we de twee voorgaande getallen van elkaar af.
n
rn=rn-1+/-rn-2
rn+1/rn
1
1
2
1
1
3
2
2
4
3
1,5
5
5
1,666667
6
-2
-0,4
7
7
-3,5
8
-9
-1,28571
9
-2
0,222222
10
-11
5,5
11
9
-0,81818
12
-2
-0,22222
Raad getal
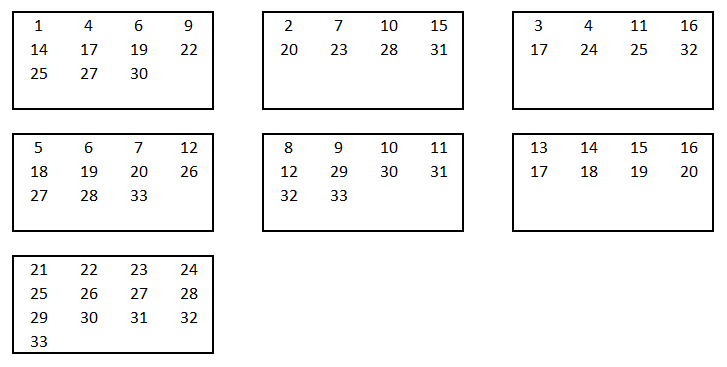
Begin met een som = 0.
Wanneer het gekozen getal op de kaart staat tel je het eerste getal bij de som op.
Na de 7e kaart is de som het gekozen getal.Tribonacci
We krijgen dus: 1, 1, 1, 3, 5, 9, 17, 31, …
Wij gaan hier gebruik maken van de zogenaamde abcd-formule (naar analogie van de abc-formule voor tweedegraads vergelijkingen).
a=1, b=-1, c=-1 en d=-1.
In ons voorbeeld zijn er geen andere reële oplossingen meer.Fibonacci gedicht
wrote
a poem
on a page
but then each line grew
by the word sum of the previous two
until I started to worry at all these words coming with such frequency
because, as you can see, it can be easy to run out of space when a poem gets all Fibonacci sequency.Driehoek van Pascal
op de tweede regel links van de 1 weer een 1 en rechts van de 1 ook een 1,
de derde regel begint weer links van de tweede regel met een 1, daarna de som van de bovenstaande getallen en eindigend met een 1,
alle regels daaronder volgen de vorige regel.
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
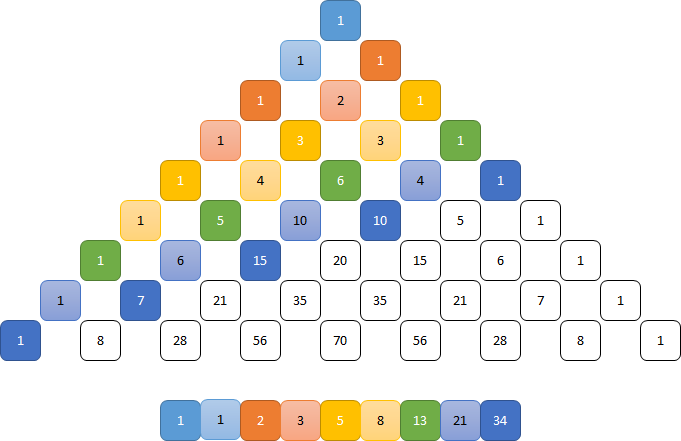
De restjes…
Deelbaarheid
Laatste cijfers
De laatste 2 cijfers van Fn ≡ Fn mod 100 als n<1000.Pisano
Zo is π(2)=3, π(3)=8, π(4)=6 etc.
π(n) is even voor n>2
Als de GGD van m en n gelijk is aan 1 dan is π(mn) gelijk aan de KGV van π(m) en π(n).Mediant
Dus de mediant van twee breuken is:Deelbaar door 3
Voorbeeld: .., 3, 5, 8, 13, 21, … (3+21)/8 = 3 en dus deelbaar door 3.
Het Fibonacci getal daarna noemen we b.
Dan krijgen we de volgende 5 Fibonacci getallen: a, b, a+b, a+2b, 2a+3b.
En daaruit volgt, volgens bovenstaande regel:Fibonacci sommen
Is een willekeurig geheel getal een Fibonacci getal?
Wanneer √(5q2+4) of √(5q2-4) een geheel getal oplevert, dan is q een Fibonacci getal.
Neem q=88 dan zijn √(5*882+4) ≈ 88,023 en √(5*882-4) ≈ 89,977 beide niet geheel en is 88 dus geen Fibonacci getal.Grootste Gemene Deler (GGD)
één negenentachtigste (1/89)
0.01
0.001
0.000 2
0.000 03
0.000 005
0.000 000 8
0.000 000 13
0.000 000 021
0.000 000 003 4
0.000 000 000 55
0.000 000 000 08 9
0.000 000 000 01 44
.
.
.
_____________________+
0.011 235 955 056… = 1/89Korte biografieën
Leonardo van Pisa
In zijn beroemde boek Liber Abaci (letterlijk: Boek van het telraam) zette hij deze Indische methode uiteen, wat voor Europa een geheel nieuwe manier van rekenen betekende.François Édouard Anatole Lucas
Jacques Philippe Marie Binet
Blaise Pascal
Programma’s
Dim w5 As Double
Dim phi As Double
Dim m1dphi As Double
phi = 0.5 + 0.5 * w5
m1dphi = (-1 / phi)
BinetInt = (phi ^ n – m1dphi ^ n) / w5
End Function
Dim w5 As Double
Dim phi As Double
Dim m1dphi As Double
phi = 0.5 + 0.5 * w5
m1dphi = (-1 / phi)
BinetLucasInt = phi ^ n + m1dphi ^ n
End Function
Dim mm As Variant
MyMod = CInt(mm)
End Function
Dim i As Long
Dim v As Double, h As Double
i = 2
v = 1
h = 1
Do
v = h
i = i + 1
h = MyMod(BinetInt(i), m)
Loop Until (v = 0 And h = 1)
Pisano = i – 1
ElseIf m = 2 Then
Pisano = 3
Else
Pisano = -1
End If
End Function
session_start();
$_SESSION[‘beurt’] = 0;
$_SESSIOM[‘som’] = 0;
$_SESSION[‘antwoord’] = ‘nee’;
?>
<head>
<link rel=”stylesheet” href=”wiskunst.css”>
<title>Ik raad uw getal</title>
</head>
$kaart2 = array(2, 7, 10, 15, 20, 23, 28, 31);
$kaart3 = array(3, 4, 11, 16, 17, 24, 25, 32);
$kaart4 = array(5, 6, 7, 12, 18, 19, 20, 26, 27, 28, 33);
$kaart5 = array(8, 9, 10, 11, 12, 29, 30, 31, 32, 33);
$kaart6 = array(13, 14, 15, 16, 17, 18, 19, 20);
$kaart7 = array(21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33);
$fib = array(1, 1, 2, 3, 5, 8, 13, 21);
{
global $kaart1, $kaart2, $kaart3, $kaart4, $kaart5, $kaart6, $kaart7;
{
$a = count($kaart1);
$kaart = $kaart1;
};
if ($nr == 2)
{
$a = count($kaart2);
$kaart = $kaart2;
};
if ($nr == 3)
{
$a = count($kaart3);
$kaart = $kaart3;
};
if ($nr == 4)
{
$a = count($kaart4);
$kaart = $kaart4;
};
if ($nr == 5)
{
$a = count($kaart5);
$kaart = $kaart5;
};
if ($nr == 6)
{
$a = count($kaart6);
$kaart = $kaart6;
};
if ($nr == 7)
{
$a = count($kaart7);
$kaart = $kaart7;
};
echo “<table border=’0′ cols=’4′ rows=’4′ width=’65%’>”;
echo “<tr height=’15px;’>”;
for ($i=0; $i<$a; $i++)
{
echo “<td width=’5%’ align=’right’>” . $kaart[$i] . “</td>”;
if (($i + 1) % 4 == 0) {
echo “</tr>”;
echo “<tr height=’15px;’>”;
}
};
echo “</table>”;
};
{
global $fib;
{
$beurt = htmlspecialchars($_GET[‘beurt’]);
};
if (isset($_GET[‘som’]))
{
$som = htmlspecialchars($_GET[‘som’]);
};
if (isset($_GET[‘antwoord’]))
{
$antwoord = htmlspecialchars($_GET[‘antwoord’]);
};
if ($beurt<1)
{
myprint(“Ik raad uw getal”);
myprint(“”);
myprint(“Kies een getal tussen 1 en 33, beide mogen meedoen.”);
myprint(“Naar aanleiding van uw antwoorden zal ik dat getal raden.”);
myprint(“”);
echo “<a href=’raadfib.php?beurt=1&som=0&antwoord=nee’>Start spel</a>”;
};
if ($beurt>=1 && $beurt<=7)
{
$g = ToonKaart($beurt);
if ($antwoord == ‘ja’)
{
$som += $fib[$beurt-1];
};
myprint(“”);
if ($beurt < 8)
{
echo “<table border=’0′ cols=’2′ rows=’1′ width=’65%’>”;
echo “<tr height=’15px;’>”;
echo “<td width=’5%’ align=’right’><a href=’raadfib.php?beurt=” . ($beurt+1) . “&som=” . $som . “&antwoord=ja’>Ja, mijn getal staat er bij</a></td>”;
echo “<td width=’5%’ align=’right’><a href=’raadfib.php?beurt=” . ($beurt+1) . “&som=” . $som . “&antwoord=nee’>Nee, mijn getal staat er niet bij</a></td>”;
echo “</tr></table>”;
};
};
if ($beurt >= 8)
{
if ($antwoord == ‘ja’)
{
$som += $fib[7];
}
myprint(“U had ” . $som . ” gekozen.”);
myprint(“”);
echo “<a href=’raadfib.php?beurt=1&som=0&antwoord=nee’>Nog eens spelen. (Anders kunt u dit venster sluiten)</a>”;
};
};
?>
<div class=”header”>
<?php myheader(“<div class=’headerfont’>Ik raad uw getal</div>”); ?>
</div>
<p>
<?php
Speel();
?>
</p>
</body>
</html>Bronnen
Lucas: https://stringfixer.com/nl/Lucas_number
Leonardo van Pisa: https://nl.wikipedia.org/wiki/Fibonacci
Fibonacci: https://nl.wikipedia.org/wiki/Rij_van_Fibonacci
Liber Abaci: https://en.wikipedia.org/wiki/Liber_Abaci
Binet: https://nl.wikipedia.org/wiki/Jacques_Philippe_Marie_Binet
Pascal: https://nl.wikipedia.org/wiki/Blaise_Pascal
Pisano figuren: https://www.youtube.com/watch?v=o1eLKODSCqw&ab_channel=JacobYatsko
Random Fibonacci: https://www.youtube.com/watch?v=ELA8gNNMHoU&ab_channel=Numberphile
Grafieken: https://www.youtube.com/watch?v=ghxQA3vvhsk&t=361s&ab_channel=Stand-upMaths
Tribonacci: https://www.youtube.com/watch?v=fMJflV_GUpU&ab_channel=Numberphile
Over bloemetjes en bijtjes
\left\{\begin{matrix}F_{1}=F_{2}=1\\F_{n}=F_{n\text{ - }1}+F_{n\text{ - }2}, \forall n>2\end{matrix}\right.
\left\{\begin{matrix}F_{0}=0, F_{1}=1\\F_{n}=F_{n\text{ - }1}+F_{n\text{ - }2}, \forall n>1\end{matrix}\right.
\frac{a}{b}=\frac{a+b}{a}\Rightarrow b(a+b)=a^{2}
a^{2}=a+1 \Rightarrow a^{2}\text{ - }a\text{ - }1=0
a=\frac{1}{2}\text{ - }\frac{1}{2}\sqrt{5}\; \vee a=\frac{1}{2}+\frac{1}{2}\sqrt{5}
\frac{1}{2}\text{ - }\frac{1}{2}\sqrt{5}
\varphi =\frac{1}{2}\text{ - }\frac{1}{2}\sqrt{5}\; en\; \phi =\frac{1}{2}+\frac{1}{2}\sqrt{5}
\varphi =\text{ - }\frac{1}{\phi }
\phi +\varphi =1\; en\; \phi \text{ - }\varphi =\sqrt{5}
B(n)=\frac{\phi ^{n}\text{ - }\varphi ^{n}}{\sqrt{5}}
x^{\text{ - }n}=\frac{1}{x^{n}}\\x^{\frac{1}{n}}=\sqrt[n]{x}
B(x), \; x\in \mathbb{R}^{+}\cup {\left \{ 0 \right \}}
\left\{\begin{matrix}a_{0}=2=\alpha \varphi ^{0}+\beta \Phi ^{0}=\alpha +\beta \\a_{1}=1=\alpha \varphi ^{1}+\beta \Phi ^{1}=\alpha \varphi +\beta \Phi \end{matrix}\right.
\left (\begin{array}{rr|r}1 & 1 & 1 \\ \varphi & \phi & -1 \\\end{array}\right ) \Rightarrow (stap1:II\text{ - }\varphi I) \left (\begin{array}{rr|r}1 & 1\;\;\;\;\; \;\;\; & 2 \;\;\;\;\;\;\\ 0 & \varphi\text{ - }\phi=\sqrt{5} & 1\text{ - }2\phi=\sqrt{5} \\\end{array}\right )
\left (\begin{array}{rr|r}1 & 1 & 2 \\ 0 & \sqrt{5} & \sqrt{5} \\\end{array}\right ) \Rightarrow (stap2:\frac{II}{\sqrt{5}}) \left (\begin{array}{rr|r}1 & 1 & 2 \\ 0 & 1 & 1\\\end{array}\right ) \Rightarrow (stap3:I\text{ - }II) \left (\begin{array}{rr|r}1 & 0 & 1 \\ 0 & 1 & 1\\\end{array}\right )
B_{L}(n)=\varphi ^{n}+\phi ^{n}=\left ( \frac{1\text{ - }\sqrt{5}}{2} \right )^{n}+\left ( \frac{1+\sqrt{5}}{2} \right )^{n}
F_{n}=\left [ \frac{\Phi ^{n}}{\sqrt{5}} \right ]=\left [ \frac{L_{n}}{\sqrt{5}} \right ]
x=\sqrt[3]{\frac{\text{ - }q+\sqrt{q^{2}+\frac{4}{27}p^{3}}}{2}}+\sqrt[3]{\frac{\text{ - }q\text{ - }\sqrt{q^{2}+\frac{4}{27}p^{3}}}{2}}\text{ - }\frac{b}{3a},\; met\; p=\frac{c}{a}\text{ - }\frac{b^{2}}{3a^{2}}\; en\; q=\frac{2b^{3}}{27a^{3}}\text{ - }\frac{bc}{3a^{2}}+\frac{d}{a}
n|m\Leftrightarrow F_{n}|F_{m}
\frac{a}{b}\oplus \frac{c}{d}=\frac{a+c}{b+d}
\frac{0}{1}\oplus\frac{1}{2}=\frac{1}{3};\frac{1}{2}\oplus\frac{1}{3}=\frac{2}{5};\frac{1}{3}\oplus\frac{2}{5}=\frac{3}{8};\frac{2}{5}\oplus\frac{3}{8}=\frac{5}{13}
\frac{0}{1},\frac{1}{2},\frac{1}{3},\frac{2}{5},\frac{3}{8},\frac{5}{13},...
3\mid \frac{a+(2a+3b)}{a+b}=\frac{3a+3b}{a+b}=\frac{3(a+b)}{a+b}=3
#Binet grafieken
import math
import matplotlib.pyplot as plt
wortel5 = math.sqrt(5)
phi = 0.5 + 0.5*wortel5
def Binet(x):
return (phi**x – (-1/phi)**x)/wortel5
def BinetLucas(x):
return phi**x + (-1/phi)**x
rfi=[]
ifi=[]
rlu=[]
ilu=[]
fib=[]
luc=[]
yas=[]
xs=-5
xe=5
for x in range(xs,xe+1):
fib.append(Binet(x))
luc.append(BinetLucas(x))
yas.append(0)
f=100
for x in range(xs*f,int((xe+0.5)*f)):
zb=Binet(x/f)
zl=BinetLucas(x/f)
rfi.append(zb.real)
ifi.append(zb.imag)
rlu.append(zl.real)
ilu.append(zl.imag)
fig, ax = plt.subplots()
#ax.set_title(‘Binet (blauwe lijn) en Fib (rode stippen)’)
#ax.set_title(‘Binet (cyane lijn) en Luc (magenta driehoekjes)’)
ax.set_title(‘Fib (blauwe lijn, rode stippen); Luc (cyaan lijn, magenta driehoekjes)’)
#ax.set_xlim(-4,4)
#ax.set_ylim(-4,4)
ax.set_xlim(-5,5)
ax.set_ylim(-4,6)
#ticks=[n for n in range(-5,9)]
ticksx=[n for n in range(-5,5)]
ticksy=[n for n in range(-4,6)]
ax.set_xticks(ticksx)
ax.set_yticks(ticksy)
ax.set_box_aspect(0.9)
ax.plot(rfi,ifi,’b’)
ax.plot(fib,yas,’ro’)
ax.plot(rlu,ilu,’c’)
ax.plot(luc,yas,’m’,marker=’^’)
ax.grid(True)
#plt.plot(r,i)
#plt.plot(fib,yas,’ro’)
#plt.grid(True)
plt.show()
print(“klaar.”)
#Pisano figuren
#bron: https://www.youtube.com/watch?v=o1eLKODSCqw&t=325s&ab_channel=JacobYatsko
import turtle as sp
import math
import random
from PIL import Image, ImageEnhance
from PIL import EpsImagePlugin
s=sp.Screen()
t=sp.Turtle()
t.hideturtle()
t.pensize(2)
t.pendown()
t.speed(0)
wortel5 = math.sqrt(5)
phi = 0.5 + 0.5*wortel5
def Binet(n):
return int((phi**n – (-1/phi)**n)/wortel5)
fnmods=[]
def MakeRange(m):
global fnmods
fnmods=[0,1]
i=1
h=1
while True:
v=h
i=i+1
h=int(Binet(i) % m)
fnmods.append(h)
if v==0 and h==1:
fnmods.pop()
fnmods.pop()
break
def DrawVertices(number):
#trek lijnen tussen hoekpunten (vertices)
a=number
h=360/a
punten=[]
numzero=0
for i in range(a+1):
t.color(‘red’)
t.circle(150,h)
t.color(‘blue’)
t.dot(10)
punten.append(t.pos())
t.color(‘magenta’)
t.pensize(1)
t.penup()
t.goto(punten[0])
t.pendown()
MakeRange(number)
for i in range(len(fnmods)):
if fnmods[i] == 0:
numzero = numzero + 1
t.goto(punten[fnmods[i]])
t.color(‘black’)
t.penup()
t.goto(-75,-30)
t.write(“Number of points: “+str(number),font=(‘Arial’,12,’normal’))
t.goto(-75,-60)
t.write(“Number of vertices: “+str(len(fnmods)),align=’left’, font=(‘Arial’,12,’normal’))
t.goto(-75,-90)
t.write(“Number of zero’s: “+str(numzero),align=’left’, font=(‘Arial’,12,’normal’))
#4 nullen: symetrisch; 1 nul: asymetrisch; 2 nullen: beide
t.goto(-75,-120)
t.write(“fibn mod “+str(number)+”: “+str(fnmods),align=’center’, font=(‘Arial’,8,’normal’))
#ts=sp.getscreen()
def DrawLines(number, step=25, repeat=1, angle=90):
#regels:
#als 0 -> doe niets
#als even -> naar rechts, vooruit
#als oneven -> naar links, vooruit
lx=0
ly=0
while angle == 0:
angle = random.uniform(-180,180)
t.color(‘black’)
t.pendown
if number > 1:
MakeRange(number)
for j in range(repeat):
for i in range(len(fnmods)):
if fnmods[i] != 0:
if fnmods[i] % 2 == 0:
t.right(angle)
t.forward(step)
else:
t.left(angle)
t.forward(step)
tx,ty=t.position()
if tx<lx:
lx=tx
if ty<ly:
ly=ty
else: #speel met Fibonacci rij
for j in range(repeat):
for i in range(13):
f = Binet(i)
if f != 0:
if f % 2 == 0:
t.right(angle)
t.forward(step)
else:
t.left(angle)
t.forward(step)
#s.delay(250)
tx,ty=t.position()
if tx<lx:
lx=tx
if ty<ly:
ly=ty
t.penup()
s=”Params: mod=”+str(number)+’; repeat=’+str(repeat)+’; angle=’+str(angle)
#print(lx,ly,len(s))
t.goto(lx,ly-25)
t.write(s,align=’left’, font=(‘Arial’,12,’normal’))
DrawVertices(19)
#DrawLines(1,repeat=1,angle=90,step=50) #align=left
#DrawLines(2,repeat=2,angle=90,step=50) #align=center
#DrawLines(3,repeat=4,angle=90,step=50) #align=left
#DrawLines(4,repeat=4,angle=90,step=50) #align=left
#DrawLines(5,repeat=1,angle=90,step=50) #align=center
#DrawLines(6,repeat=2,angle=90,step=50) #align=left
#DrawLines(7,repeat=3,angle=90,step=50) #align=left
#DrawLines(8,repeat=2,angle=90,step=50) #align=left
#DrawLines(9,repeat=2,angle=90,step=25) #align=left
#DrawLines(9,repeat=3,angle=100,step=25) #align=left
#DrawLines(10,repeat=1,angle=90,step=50) #align=left
#DrawLines(11,repeat=4,angle=90,step=50) #align=left
#DrawLines(12,repeat=2,angle=90,step=50) #align=left
#DrawLines(13,repeat=2,angle=90,step=25) #align=left
#DrawLines(14,repeat=2,angle=90,step=50) #align=left
#DrawLines(15,repeat=3,angle=90,step=25) #align=left
#DrawLines(16,repeat=2,angle=90,step=50) #align=left
#DrawLines(17,repeat=2,angle=90,step=25) #align=left
#DrawLines(18,repeat=2,angle=90,step=50) #align=left
#DrawLines(19,repeat=4,angle=90,step=25) #align=left
#DrawLines(20,repeat=2,angle=90,step=50) #align=left
#DrawLines(21,repeat=3,angle=90,step=50) #align=left
#DrawLines(22,repeat=4,angle=90,step=50) #align=left
#DrawLines(23,repeat=2,angle=90,step=25) #align=left
#DrawLines(24,repeat=2,angle=90,step=50) #align=left
sp.done()