Inhoud De driehoek van Pascal is een wiskundige curiositeit maar tevens ook een (zeer) handige tool bij het bepalen van kansen. Net zoals de stelling van Pythagoras niet door Pythagoras is ontdekt is de Driehoek van Pascal niet door Pascal ontdekt. In dit artikel gaan we kijken naar hoe de driehoek wordt gemaakt en welke zaken we in de driehoek allemaal kunnen terugvinden. Om de driehoek te maken beginnen we bovenaan, in de top dus, met het noteren van een 1: 1 Daaronder zetten we links van de 1 weer een 1 en rechts daarvan ook weer een 1: 1 De derde regel zetten we weer een regel lager en beginnen weer met een 1, daarna steeds de som van de twee bovenliggende getallen (eentje links daarboven een eentje rechts daarboven, om weer met een 1 te eindigen: 1 En zo verder: 1 Afspraken: Merk op dat de driehoek symmetrisch is. Er loopt als het ware een verticale lijn door het midden dat beide kanten spiegelt. In willekeurige volgorde volgen een aantal eigenschappen van de driehoek van Pascal Veel plezier. Wanneer je van iedere rij de som van de getallen bepaalt dan zie je, hopelijk, bekende uitkomsten: 1, 2, 4, 8, 16, 32… Inderdaad, allemaal machten van 2. Meer bepaald: 2 tot de macht rij-nummer: Dus de som van de getallen op rij n = 2n. In formulevorm: Als je van iedere rij de getallen achter elkaar zet en dit ziet als een nieuw getal, dan is dat een macht van 11. Kijk maar Rij 0: 1 = 110 Bij rij 5 gaat dit ook op, mits je de getallen beperkt tot 1 cijfer en daar waar nodig, dus bij 2 cijfers, het eerste cijfer “overhaalt” naar links. Dus rij 5: 15(10)(10)51 wordt dan 161051. Van de eerste (linker) 10 wordt de 1 naar links overgehaald waardoor de 5 dus een 6 wordt. De 0 blijft achter. Echter de tweede 10 moet ook weer naar links worden overgehaald, dus de 0 wordt een 1, waarna er een 0 overblijft gevolgd door de laatste 51. Etcetera. De buitenste diagonalen bestaan louter uit 1-en. Op de een-na-buitenste diagonalen staan de natuurlijke getallen: We mogen dus concluderen dat alle natuurlijke getallen voorkomen in de driehoek! Gaan we weer een diagonaal naar binnen, dan krijgen we de zogenaamde driehoeksgetallen: 1, 3, 6, 10, 15, 21, …: Een driehoeksgetal geeft aan hoeveel stippen je nodig hebt om een driehoek met basis n (stippen) te maken. o heeft dus 10 stippen. Nog een diagonaal naar binnen levert de zogenaamde tetraëdrische getallen op: 1, 4, 10, 20, 35, 56, …: Een teraëdrisch getal geeft aan hoeveel “knikkers” je nodig hebt om een piramide met zijde n (knikkers) te bouwen. Ook de Fibonacci getallen zitten in de driehoek (zie ook het artikel Over bloemetjes en bijtjes): 1, 1, 2, 3, 5, 8, 13, …: Wanneer je een aantal getallen op een diagonaal (beginnend bij de rand, dus bij 1) van links boven naar rechts onder bij elkaar optelt dan is de som het getal dat er 1 positie naar links onder staat: Dus in bovenstaande afbeelding: 1+2+3 = 6 en 1+5+15+35 = 56. Je krijgt dus een soort hockeystick als figuur. De andere kant op, dus van rechtsboven naar links onder en dan eentje naar rechts onder werkt natuurlijk ook omdat de driehoek symmetrisch is. Op de middelbare school, bij het vak wiskunde, heeft u ongetwijfeld te maken gehad met zogenaamde merkwaardige producten. Eén daarvan luidde: (a+b)2 en zonder dat uit te werken moest u dan weten dat de uitkomst hiervan a2+2ab+b2 is. Maar laten we eens een stapje verder gaan. Om te beginnen met uitwerkingen: (a+b)3 = (a+b)(a+b)2 = (a+b)(a2+2ab+b2) = a3+2a2b+ab2+ba2+2ab2+b3 = a3+3a2b+3ab2+b3. En als u nog geen patroon ziet ontstaan dan nodig ik u van harte uit om zelf (a+b)5 met de hand uit te rekenen. Kijken we naar de factoren van (a+b)3 dan zien we 1, 3, 3 en 1. En die van (a+b)4 zijn 1, 4, 6, 4, 1. En dit zijn precies de getallen uit de driehoek van respectievelijk rij 3 en rij 4. Tevens zien we dat de exponenten van a aflopen van n naar nul en die van b oplopen van 0 tot n. Als we bovenstaande, letterlijk, toepassen op (a+b)5 dan krijgen we: (a+b)5 = 1a5b0 + 5a4b1 + 10a3b2 + 10a2b3 + 5a1b4 + 1a0b5, en omdat we de factor 1 en de macht 1 altijd weglaten en iets tot de macht 0 altijd 1 is (behalve 00) krijgen we dus: (a+b)5 = a5 +5a4b + 10a3b2 + 10a2b3 +5ab4 + b5. De algemene formule voor bovenstaande volgt in de volgende paragraaf. We beginnen met een voorbeeld: Op hoeveel manieren kunnen een directeur en een onderdirecteur worden gekozen uit 5 gekwalificeerde mensen? Stel dat de mensen respectievelijk Anton, Bea, Christine, Dirk en Eveline heten dan zijn de volgende combinaties mogelijk: Anton – Bea, Merk op dat het niet uitmaakt of we het hebben over Anton – Dirk of Dirk – Anton. Er zijn dus 10 combinaties mogelijk en dat is precies P5,2. En dat is ook juist: Het aantal combinaties van x elementen uit totaal y mogelijkheden is Px,y. Het aantal combinaties wordt Binomiaal coëfficiënt genoemd en heeft een formele notatie en een formule: en spreek je uit als “n boven k”. Opgemerkt moet worden dat n ≥ k is. n! spreek je uit als “n faculteit” en is niets anders dan het product van 1 t/m n. Dus 5! = 1 x 2 x 3 x 4 x 5 = 120. Het leuke is dus dat:Inleiding
Geschriften uit de 10e eeuw uit India en Perzië (Iran) en uit de 13e eeuw uit China maken al melding van de driehoek.
In de 16e eeuw wordt door de Duitser Peter Apian de driehoek genoemd.
En in de 17e eeuw maakt Pascal gebruik van de driehoek on zijn verhandelingen over kansberekening.
In de 18e eeuw werd de driehoek, door onder andere de Moivre vernoemd naar Pascal.
Overigens vindt je in Zuid Europa ook de naam: Driehoek van Tartaglia (o.a. in Italië), omdat hij de driehoek ook gebruikte.
Bewijzen laat ik achterwege. Op het internet zijn er genoeg te vinden…De driehoek maken
1 1
1 1
1 2 1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
…
En in z’n algemeenheid: Pn,0=Pn,n=1 en Pn,m=Pn-1,m-1+Pn-1,m, voor 1 ≤ n,m ≤ n-1.Som van de rijen
rij
som
0
1
1
1
1
1
2
2
1
2
1
4
3
1
3
3
1
8
4
1
4
6
4
1
16
5
1
5
10
10
5
1
32
6
1
6
15
20
15
6
1
64
7
1
7
21
35
35
21
7
1
128
8
1
8
28
56
70
56
28
8
1
256
9
1
9
36
84
126
126
84
36
9
1
512
Machten van 11
Rij 1: 11 = 111
Rij 2: 121 = 112
Rij 3: 1331 = 113
Rij 4: 14641 = 114
En ook dit getal, 161051 is een macht van 11, namelijk 115.Diagonalen
Natuurlijke getallen
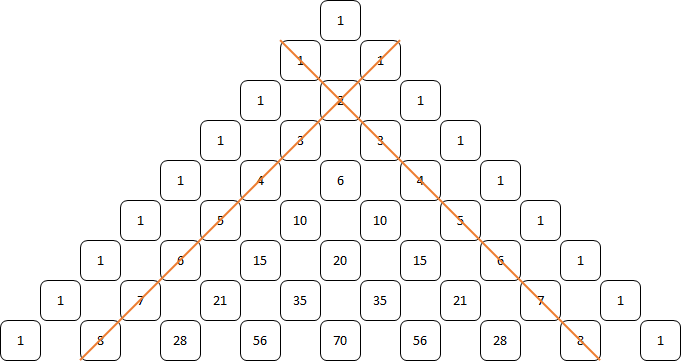
Driehoeks getallen
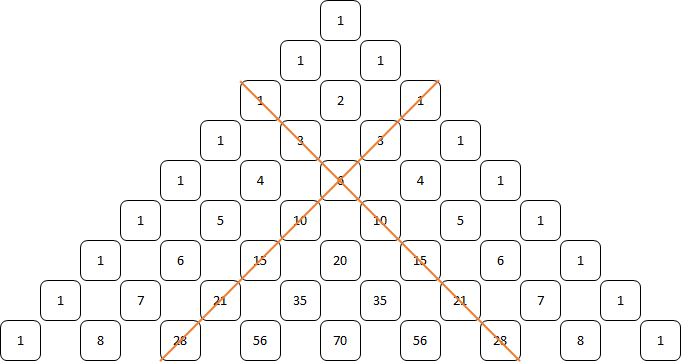
Bijvoorbeeld een driehoek met basis 4:
o o
o o o
o o o oTetraëdrische getallen
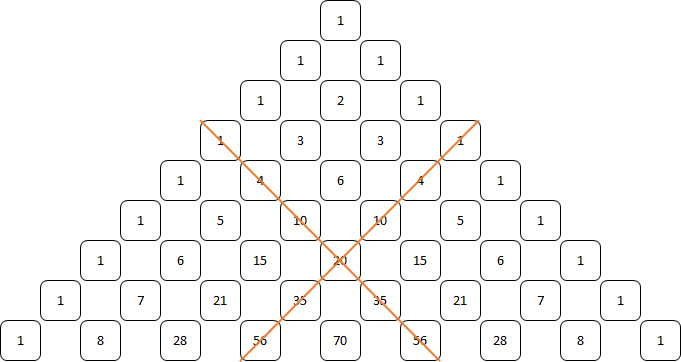
Fibonacci getallen
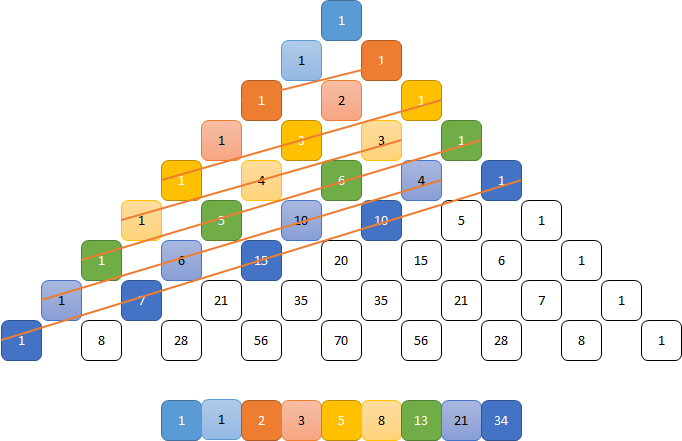
Hockeystick
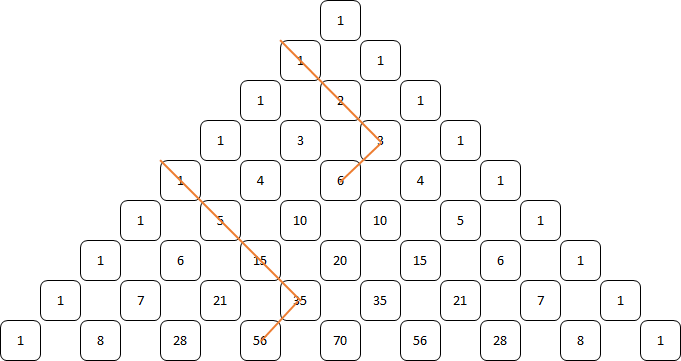
Merkwaardige producten
(a+b)4 = (a+b)(a+b)3 = (a+b)(a3+3a2b+3ab2+b3) = … = a4+4a3b+6a2b2+4ab3+b4.Binomiaal coëfficiënten
Anton – Christine,
Anton – Dirk,
Anton – Eveline,
Bea – Christine,
Bea – Dirk,
Bea – Eveline,
Christine – Dirk,
Christine – Eveline,
Dirk en Eveline.
Dus kan de driehoek nu ook als volgt worden geschreven:
Nog even terugkomend op de vorige paragraaf. De coëfficiënten van de ontwikkeling van (a+b)n vinden we dus terug in de ne rij van de driehoek. Maar de getallen die daar staan kunnen dus ook worden gevormd door de binomiaal coëfficiënten. En daarmee verkrijgen we dan de volgende formule:
Sierpinski
Sierpinski is, buiten een naam van Poolse wiskundige (19e/20e eeuw), de naam van een fractalachtige figuur bestaande uit zichzelf herhalende driehoeken.
En jawel, deze fractal zit in de driehoek.
Wanneer je alle even getallen verwijderd en alle oneven getallen vervangt door een symbool (bijvoorbeeld een o) dan krijg je onderstaande figuur:

Hierboven dus een representatie van de eerste 32 rijen met alleen de oneven getallen.
Priemen
Wanneer het eerste element van een rij van de driehoek een priemgetal is, dan zijn alle andere getallen van die rij een veelvoud van dat priemgetal:
| 1 | ||||||||||||||||||||||
| 1 | 1 | |||||||||||||||||||||
| 1 | 2 | 1 | ||||||||||||||||||||
| 1 | 3 | 3 | 1 | |||||||||||||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||||||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||||||||||||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |||||||||||||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | ||||||||||||
| 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 |
Het eerste getal van rij 3 is een 3, het volgende getal, ook 3, is dus deelbaar door 3, namelijk 3 = 1×3.
Het eerste getal van rij 5 is een 5. Alle volgende getallen zijn deelbaar door 5: 10=2×5, 10=2×5, 5=1×5.
Het eerste getal van rij 7 is een 7. En dus 21=3×7, 35=5×7, 35=5×7, 21=3×7, 7=1×7.
En voor rij 11: 55=5×11, 165=15×11, 330=30×11, 462=42×11 etc.
In formule vorm:
Om te kijken of een getal priem is kun je nu ook gebruik maken van bovenstaande kennis.
Neem een getal Pn,1. Als alle andere getallen op die regel deelbaar zijn door Pn,1 dan is Pn,1 priem, anders niet. Dus wanneer je ook maar één getal op die regel vindt die niet deelbaar is door Pn,1, dan is Pn,1 niet priem!
π
Het getal π is ook terug te vinden in de driehoek.
We gebruiken daarvoor de diagonaal van de driehoeksgetallen (zie hierboven), dat zijn: 1, 3, 6, 10, 15, 21, 28, 36, 45, …
Als we deze getallen omzetten in hun reciproke (dus 1 gedeeld door dat getal) en tellen ze paarsgewijs op en daarna paarsgewijs af dan krijg je een limiet die naar π-2 gaat. Dus:
Deze prachtige ontdekking is gedaan door Jonas Castillo Toloza in 2007.
Met behulp van Excel ben ik tot rij 124 gegaan (7626) en dan is de uitkomst (van de limiet tot daartoe) 3,141594…
Er bestaan ook nog andere manieren om vanuit de driehoek π te verkrijgen of te benaderen, maar dit is tot nog toe wel de mooiste!
e
Ook het getal van Euler, e, zit in de driehoek verscholen. In dit geval wel goed verscholen!
Wanneer En het product is van de getallen van rij n van de driehoek dan:
En er geldt dat:
Samengestelde rente
Wat is het eindsaldo bij een eerste inleg van € 1000,= tegen 10% per jaar (waar zijn de tijden gebleven???) met een looptijd van 2 jaar?
Dat is een vrij eenvoudige opgaven maar dit is even puur ter illustratie.
In een tabelletje is dit zo uitgerekend:
| jaar | bedrag |
| 0 | 1000 |
| 1 | 1000+100=1100 |
| 2 | 1000+110=1210 |
Maar dit kunnen we ook als volgt met de driehoek berekenen.
De looptijd is 2 jaar dus pakken we de getallen van rij 2 van de driehoek:
1 2 1
Onder het eerste getal zetten we de inleg. Onder de volgende getallen de opeenvolgende rentes van het vorige getal:
1 2 1
1000 100(=10%x1000) 10(=10%x100)
Op de volgende regel vermenigvuldigen we de getallen die daarboven staan:
1 2 1
1000 100 10
1000(=1×1000) 200(=2×100) 10(=1×10)
Tot slot tellen we de getallen van de onderste regel bij elkaar op:
1 2 1
1000 100 10
1000+200+10 = 1210
En voilà, daar is ons eindbedrag!
Nog een voorbeeld: Wat is het eindbedrag na 3 jaar bij een inleg van € 8000 tegen 5% rente per jaar?
We nemen de getallen van rij 3 van de driehoek en rekenen daarmee als volgt:
1 3 3 1
8000 400(5%x8000) 20(5%x400) 1(5%x20)
8000 + 1200 + 60 + 1 = 9261
Dus het eindbedrag is € 9261
Overige feitjes
Kijken we nog even naar de eerste 4 rijen van de driehoek:
| rij | ||||||||
| 0 | 1 | |||||||
| 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 1 | |||||
| 3 | 1 | 3 | 3 | 1 | ||||
Zoals we eerder hebben opgemerkt is de driehoek symmetrisch, dus Pn,m = Pm,n-m.
Maar dan geldt dus ook:
De som van twee opeenvolgende driehoeksgetallen is gelijk aan het kwadraat van het rijnummer van het kleinste van de twee.
Dus Pn,2+Pn+1,2=n2.
Maar dan geldt ook:
Nog een leuk feitje: De som van de kwadraten van de getallen op rij n is gelijk aan het getal in het “midden” van rij 2n:
| n | ||||||||||||||||||
| 0 | 1 | |||||||||||||||||
| 1 | 1 | 1 | ||||||||||||||||
| 2 | 1 | 2 | 1 | |||||||||||||||
| 3 | 1 | 3 | 3 | 1 | ||||||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | |||||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | ||||||||||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | |||||||||||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||||||||
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Hierboven geldt: 12+42+62+42+12=70.
In formule vorm:
ofwel:
Statistieken
Even/oneven
Wanneer je een beetje willekeurig naar de driehoek kijkt dan valt het wellicht op dat er meer even getallen dan oneven getallen zijn.
Met een simpel Python programmaatje ben ik dat eens nagegaan en heb me daarna afgevraagd of de verhouding tussen even en oneven getallen wellicht naar een limiet gaan.
De conclusies (tot zover en slechts proefondervindelijk verkregen) zijn dat er inderdaad (veel!) meer even getallen dan oneven getallen voorkomen en dat de verhouding tussen beiden niet naar een limiet gaan:
| aantal rijen | aantal even | aantal oneven | oneven/even |
| 100 | 3799 | 1250 | 0,329033956 |
| 250 | 25582 | 5792 | 0,226409194 |
| 500 | 107871 | 17378 | 0,161099832 |
| 750 | 251796 | 29828 | 0,118460976 |
| 1000 | 448363 | 52136 | 0,116280781 |
| 1250 | 713544 | 68330 | 0,095761439 |
| 1500 | 1036263 | 89486 | 0,086354526 |
| 1750 | 1417354 | 114770 | 0,080974831 |
| 2000 | 1844589 | 156410 | 0,084793957 |
| 3000 | 4233039 | 268460 | 0,063420157 |
| 4000 | 7532767 | 469232 | 0,062292117 |
| 5000 | 11887521 | 614978 | 0,051733074 |
Deze resultaten en conclusies gelden alleen voor eindige driehoeken, dus driehoeken met een eindig aantal regels.
Voor een oneindige driehoek (wat de driehoek van Pascal eigenlijk ook is) geldt dit natuurlijk niet, dan zijn er evenveel even als oneven getallen. Net zoveel als de natuurlijke getallen (zie ook het artikel over Oneindig).
3003
Wanneer je gaat kijken naar de frequentie van getallen in de driehoek, dus hoe vaak een getal voorkomt in de driehoek, dan bestaat het vermoeden dat 3003 de hoogste frequentie heeft, namelijk 8.
Wederom met een simpel Python programma ben ik dit eens gaan onderzoeken, wederom proefondervindelijk.
Het programma genereert 3004 rijen en bepaalt van ieder getal hoe vaak het voorkomt in die rijen; voor zover dat getal niet een vooraf bepaald maximum (250 miljoen) overschrijdt. Dit laatste is wel een belangrijke voorwaarde, want het grootste getal dat in die 3004 rijen voorkomt bestaat uit maar liefst 903(!) cijfers.
monstrueus getal 143261974742825012529446926926548620661312654537132560320169979562365220187395844626213110169343685299650199875444071207392680132395177197815113409624662878255522728672874938324862088179712426356789244447018069250678924719811385762422784504049852576988205635141739508753459298970283808261514861429033355502909981208946101894931444994335134219729420021759926977181758445750934230561649030976709030679154571938285589217399164017822577932214232902139712625959817126591623858846188665130841746478202901971774267333133640853244550438177803782176867102861761982322066279299010181628608490400619818611255938735211537632872401028635674129310156970848110240493807691915241458482223746141295452420084632642377088715673689694885365910732898545179163729879790114315197628129684999981930621180361914428022014835228729837556586311786826305087849671118761032902185886367564857653834803737224398246102109149179583811968
Het programma toon ook een frequentie tabel (tot 250 miljoen) en daaruit blijkt dat de meeste getallen 2 maal voorkomen.
frequenties (tot 250 miljoen) 2 1; 3 2; 4 2; 5 2; 6 3; 7 2; 8 2; 9 2; 10 4; 11 2; 12 2; 13 2; 14 2; 15 4; 16 2; 17 2; 18 2; 19 2; 20 3; 21 4; 22 2; 23 2; 24 2; 25 2; 26 2; 27 2; 28 4; 29 2; 30 2; 31 2; 32 2; 33 2; 34 2; 35 4; 36 4; 37 2; 38 2; 39 2; 40 2; 41 2; 42 2; 43 2; 44 2; 45 4; 46 2; 47 2; 48 2; 49 2; 50 2; 51 2; 52 2; 53 2; 54 2; 55 4; 56 4; 57 2; 58 2; 59 2; 60 2; 61 2; 62 2; 63 2; 64 2; 65 2; 66 4; 67 2; 68 2; 69 2; 70 3; 71 2; 72 2; 73 2; 74 2; 75 2; 76 2; 77 2; 78 4; 79 2; 80 2; 81 2; 82 2; 83 2; 84 4; 85 2; 86 2; 87 2; 88 2; 89 2; 90 2; 91 4; 92 2; 93 2; 94 2; 95 2; 96 2; 97 2; 98 2; 99 2; 100 2; 101 2; 102 2; 103 2; 104 2; 105 4; 106 2; 107 2; 108 2; 109 2; 110 2; 111 2; 112 2; 113 2; 114 2; 115 2; 116 2; 117 2; 118 2; 119 2; 120 6; 121 2; 122 2; 123 2; 124 2; 125 2; 126 4; 127 2; 128 2; 129 2; 130 2; 131 2; 132 2; 133 2; 134 2; 135 2; 136 4; 137 2; 138 2; 139 2; 140 2; 141 2; 142 2; 143 2; 144 2; 145 2; 146 2; 147 2; 148 2; 149 2; 150 2; 151 2; 152 2; 153 4; 154 2; 155 2; 156 2; 157 2; 158 2; 159 2; 160 2; 161 2; 162 2; 163 2; 164 2; 165 4; 166 2; 167 2; 168 2; 169 2; 170 2; 171 4; 172 2; 173 2; 174 2; 175 2; 176 2; 177 2; 178 2; 179 2; 180 2; 181 2; 182 2; 183 2; 184 2; 185 2; 186 2; 187 2; 188 2; 189 2; 190 4; 191 2; 192 2; 193 2; 194 2; 195 2; 196 2; 197 2; 198 2; 199 2; 200 2; 201 2; 202 2; 203 2; 204 2; 205 2; 206 2; 207 2; 208 2; 209 2; 210 6; 211 2; 212 De getallen die vaker voorkomen zijn: 6 (komt 3 keer voor), 10 (komt 4 keer voor), 120 (komt 6 keer voor) en inderdaad 3003 komt 8 keer voor. Merk op dat de frequenties van 6, 10, 120 en 3003 ook de daadwerkelijke waardes zijn, want een getal n kan slechts voorkomen tot en met de ne regel in de driehoek. Met deze pagina kunt u een driehoek van Pascal genereren.
2; 213 2; 214 2; 215 2; 216 2; 217 2; 218 2; 219 2; 220 4; 221 2; 222 2; 223 2; 224 2; 225 2; 226 2; 227 2; 228 2; 229 2; 230 2; 231 4; 232 2; 233 2; 234 2; 235 2; 236 2;
237 2; 238 2; 239 2; 240 2; 241 2; 242 2; 243 2; 244 2; 245 2; 246 2; 247 2; 248 2; 249 2; 250 2; 251 2; 252 3; 253 4; 254 2; 255 2; 256 2; 257 2; 258 2; 259 2; 260 2; 261 2; 262 2; 263 2; 264 2; 265 2; 266 2; 267 2; 268 2; 269 2; 270 2; 271 2; 272 2; 273 2; 274 2; 275 2; 276 4; 277 2; 278 2; 279 2; 280 2; 281 2; 282 2; 283 2; 284 2; 285 2; 286 4; 287 2; 288 2; 289 2; 290 2; 291 2; 292 2; 293 2; 294 2; 295 2; 296 2; 297 2; 298 2; 299 2; 300 4; 301 2; 302 2; 303 2; 304 2; 305 2; 306 2; 307 2; 308 2; 309 2; 310 2; 311 2; 312 2; 313 2; 314 2; 315 2; 316 2; 317 2; 318 2; 319 2; 320 2; 321 2; 322 2; 323 2; 324 2; 325 4; 326 2; 327 2; 328 2; 329 2; 330 4; 331 2; 332 2; 333 2; 334 2; 335 2; 336 2; 337 2; 338 2; 339 2; 340 2; 341 2; 342 2; 343 2; 344 2; 345 2; 346 2; 347 2; 348 2; 349 2; 350 2; 351 4; 352 2; 353 2; 354 2; 355 2; 356 2; 357 2; 358 2; 359 2; 360 2; 361 2; 362 2; 363 2; 364 4; 365 2; 366 2; 367 2; 368 2; 369 2; 370 2; 371 2; 372 2; 373 2; 374 2; 375 2; 376 2; 377 2; 378 4; 379 2; 380 2; 381 2; 382 2; 383
2; 384 2; 385 2; 386 2; 387 2; 388 2; 389 2; 390 2; 391 2; 392 2; 393 2; 394 2; 395 2; 396 2; 397 2; 398 2; 399 2; 400 2; 401 2; 402 2; 403 2; 404 2; 405 2; 406 4; 407 2;
408 2; 409 2; 410 2; 411 2; 412 2; 413 2; 414 2; 415 2; 416 2; 417 2; 418 2; 419 2; 420 2; 421 2; 422 2; 423 2; 424 2; 425 2; 426 2; 427 2; 428 2; 429 2; 430 2; 431 2; 432 2; 433 2; 434 2; 435 4; 436 2; 437 2; 438 2; 439 2; 440 2; 441 2; 442 2; 443 2; 444 2; 445 2; 446 2; 447 2; 448 2; 449 2; 450 2; 451 2; 452 2; 453 2; 454 2; 455 4; 456 2; 457 2; 458 2; 459 2; 460 2; 461 2; 462 4; 463 2; 464 2; 465 4; 466 2; 467 2; 468 2; 469 2; 470 2; 471 2; 472 2; 473 2; 474 2; 475 2; 476 2; 477 2; 478 2; 479 2; 480 2; 481 2; 482 2; 483 2; 484 2; 485 2; 486 2; 487 2; 488 2; 489 2; 490 2; 491 2; 492 2; 493 2; 494 2; 495 4; 496 4; 497 2; 498 2; 499 2; 500 2; 501 2; 502 2; 503 2; 504 2; 505 2; 506 2; 507 2; 508 2; 509 2; 510 2; 511 2; 512 2; 513 2; 514 2; 515 2; 516 2; 517 2; 518 2; 519 2; 520 2; 521 2; 522 2; 523 2; 524 2; 525 2; 526 2; 527 2; 528 4; 529 2; 530 2; 531 2; 532 2; 533 2; 534 2; 535 2; 536 2; 537 2; 538 2; 539 2; 540 2; 541 2; 542 2; 543 2; 544 2; 545 2; 546 2; 547 2; 548 2; 549 2; 550 2; 551 2; 552 2; 553 2; 554
2; 555 2; 556 2; 557 2; 558 2; 559 2; 560 4; 561 4; 562 2; 563 2; 564 2; 565 2; 566 2; 567 2; 568 2; 569 2; 570 2; 571 2; 572 2; 573 2; 574 2; 575 2; 576 2; 577 2; 578 2;
579 2; 580 2; 581 2; 582 2; 583 2; 584 2; 585 2; 586 2; 587 2; 588 2; 589 2; 590 2; 591 2; 592 2; 593 2; 594 2; 595 4; 596 2; 597 2; 598 2; 599 2; 600 2; 601 2; 602 2; 603 2; 604 2; 605 2; 606 2; 607 2; 608 2; 609 2; 610 2; 611 2; 612 2; 613 2; 614 2; 615 2; 616 2; 617 2; 618 2; 619 2; 620 2; 621 2; 622 2; 623 2; 624 2; 625 2; 626 2; 627 2; 628 2; 629 2; 630 4; 631 2; 632 2; 633 2; 634 2; 635 2; 636 2; 637 2; 638 2; 639 2; 640 2; 641 2; 642 2; 643 2; 644 2; 645 2; 646 2; 647 2; 648 2; 649 2; 650 2; 651 2; 652 2; 653 2; 654 2; 655 2; 656 2; 657 2; 658 2; 659 2; 660 2; 661 2; 662 2; 663 2; 664 2; 665 2; 666 4; 667 2; 668 2; 669 2; 670 2; 671 2; 672 2; 673 2; 674 2; 675 2; 676 2; 677 2; 678 2; 679 2; 680 4; 681 2; 682 2; 683 2; 684 2; 685 2; 686 2; 687 2; 688 2; 689 2; 690 2; 691 2; 692 2; 693 2; 694 2; 695 2; 696 2; 697 2; 698 2; 699 2; 700 2; 701 2; 702 2; 703 4; 704 2; 705 2; 706 2; 707 2; 708 2; 709 2; 710 2; 711 2; 712 2; 713 2; 714 2; 715 4; 716 2; 717 2; 718 2; 719 2; 720 2; 721 2; 722 2; 723 2; 724 2; 725
2; 726 2; 727 2; 728 2; 729 2; 730 2; 731 2; 732 2; 733 2; 734 2; 735 2; 736 2; 737 2; 738 2; 739 2; 740 2; 741 4; 742 2; 743 2; 744 2; 745 2; 746 2; 747 2; 748 2; 749 2;
750 2; 751 2; 752 2; 753 2; 754 2; 755 2; 756 2; 757 2; 758 2; 759 2; 760 2; 761 2; 762 2; 763 2; 764 2; 765 2; 766 2; 767 2; 768 2; 769 2; 770 2; 771 2; 772 2; 773 2; 774 2; 775 2; 776 2; 777 2; 778 2; 779 2; 780 4; 781 2; 782 2; 783 2; 784 2; 785 2; 786 2; 787 2; 788 2; 789 2; 790 2; 791 2; 792 4; 793 2; 794 2; 795 2; 796 2; 797 2; 798 2; 799 2; 800 2; 801 2; 802 2; 803 2; 804 2; 805 2; 806 2; 807 2; 808 2; 809 2; 810 2; 811 2; 812 2; 813 2; 814 2; 815 2; 816 4; 817 2; 818 2; 819 2; 820 4; 821 2; 822 2; 823 2; 824 2; 825 2; 826 2; 827 2; 828 2; 829 2; 830 2; 831 2; 832 2; 833 2; 834 2; 835 2; 836 2; 837 2; 838 2; 839 2; 840 2; 841 2; 842 2; 843 2; 844 2; 845 2; 846 2; 847 2; 848 2; 849 2; 850 2; 851 2; 852 2; 853 2; 854 2; 855 2; 856 2; 857 2; 858 2; 859 2; 860 2; 861 4; 862 2; 863 2; 864 2; 865 2; 866 2; 867 2; 868 2; 869 2; 870 2; 871 2; 872 2; 873 2; 874 2; 875 2; 876 2; 877 2; 878 2; 879 2; 880 2; 881 2; 882 2; 883 2; 884 2; 885 2; 886 2; 887 2; 888 2; 889 2; 890 2; 891 2; 892 2; 893 2; 894 2; 895 2; 896
2; 897 2; 898 2; 899 2; 900 2; 901 2; 902 2; 903 4; 904 2; 905 2; 906 2; 907 2; 908 2; 909 2; 910 2; 911 2; 912 2; 913 2; 914 2; 915 2; 916 2; 917 2; 918 2; 919 2; 920 2;
921 2; 922 2; 923 2; 924 3; 925 2; 926 2; 927 2; 928 2; 929 2; 930 2; 931 2; 932 2; 933 2; 934 2; 935 2; 936 2; 937 2; 938 2; 939 2; 940 2; 941 2; 942 2; 943 2; 944 2; 945 2; 946 4; 947 2; 948 2; 949 2; 950 2; 951 2; 952 2; 953 2; 954 2; 955 2; 956 2; 957 2; 958 2; 959 2; 960 2; 961 2; 962 2; 963 2; 964 2; 965 2; 966 2; 967 2; 968 2; 969 4; 970 2; 971 2; 972 2; 973 2; 974 2; 975 2; 976 2; 977 2; 978 2; 979 2; 980 2; 981 2; 982 2; 983 2; 984 2; 985 2; 986 2; 987 2; 988 2; 989 2; 990 4; 991 2; 992 2; 993 2; 994 2; 995 2; 996 2; 997 2; 998 2; 999 2; 1000 2; 1001 4; 1002 2; 1003 2; 1004 2; 1005 2; 1006 2; 1007 2; 1008 2; 1009 2; 1010 2; 1011 2; 1012 2; 1013 2; 1014 2; 1015 2; 1016 2; 1017 2; 1018 2; 1019 2; 1020 2; 1021 2; 1022 2; 1023 2; 1024 2; 1025 2; 1026 2; 1027 2; 1028 2; 1029 2; 1030 2; 1031 2; 1032 2; 1033 2; 1034 2; 1035 4; 1036 2; 1037 2; 1038 2; 1039 2; 1040 2; 1041 2; 1042 2; 1043 2; 1044 2; 1045 2; 1046 2; 1047 2; 1048 2; 1049 2; 1050 2; 1051 2; 1052 2; 1053 2; 1054 2; 1055 2; 1056 2; 1057 2; 1058 2; 1059 2; 1060 2; 1061 2; 1062 2; 1063 2; 1064 2; 1065 2; 1066 2; 1067 2; 1068 2; 1069 2; 1070 2; 1071 2; 1072 2; 1073 2; 1074 2; 1075 2; 1076 2; 1077 2; 1078 2; 1079 2; 1080 2; 1081 4; 1082 2; 1083 2; 1084 2; 1085 2; 1086 2; 1087 2; 1088 2; 1089 2; 1090 2; 1091 2; 1092 2; 1093 2; 1094 2; 1095 2; 1096 2; 1097 2; 1098 2; 1099 2; 1100 2; 1101 2; 1102 2; 1103 2; 1104 2; 1105 2; 1106 2; 1107 2; 1108 2; 1109 2; 1110 2; 1111 2; 1112 2; 1113 2; 1114 2; 1115 2; 1116 2; 1117 2; 1118 2; 1119 2; 1120 2; 1121 2; 1122 2; 1123 2; 1124 2; 1125 2; 1126 2; 1127 2; 1128 4; 1129 2; 1130 2; 1131 2; 1132 2; 1133 2; 1134 2; 1135 2; 1136 2; 1137 2; 1138 2; 1139 2; 1140 4; 1141 2; 1142 2; 1143 2; 1144
2; 1145 2; 1146 2; 1147 2; 1148 2; 1149 2; 1150 2; 1151 2; 1152 2; 1153 2; 1154 2; 1155 2; 1156 2; 1157 2; 1158 2; 1159 2; 1160 2; 1161 2; 1162 2; 1163 2; 1164 2; 1165 2;
1166 2; 1167 2; 1168 2; 1169 2; 1170 2; 1171 2; 1172 2; 1173 2; 1174 2; 1175 2; 1176 4; 1177 2; 1178 2; 1179 2; 1180 2; 1181 2; 1182 2; 1183 2; 1184 2; 1185 2; 1186 2; 1187 2; 1188 2; 1189 2; 1190 2; 1191 2; 1192 2; 1193 2; 1194 2; 1195 2; 1196 2; 1197 2; 1198 2; 1199 2; 1200 2; 1201 2; 1202 2; 1203 2; 1204 2; 1205 2; 1206 2; 1207 2; 1208 2; 1209 2; 1210 2; 1211 2; 1212 2; 1213 2; 1214 2; 1215 2; 1216 2; 1217 2; 1218 2; 1219 2; 1220 2; 1221 2; 1222 2; 1223 2; 1224 2; 1225 4; 1226 2; 1227 2; 1228 2; 1229 2; 1230 2; 1231 2; 1232 2; 1233 2; 1234 2; 1235 2; 1236 2; 1237 2; 1238 2; 1239 2; 1240 2; 1241 2; 1242 2; 1243 2; 1244 2; 1245 2; 1246 2; 1247 2; 1248 2; 1249 2; 1250 2; 1251 2; 1252 2; 1253 2; 1254 2; 1255 2; 1256 2; 1257 2; 1258 2; 1259 2; 1260 2; 1261 2; 1262 2; 1263 2; 1264 2; 1265 2; 1266 2; 1267 2; 1268 2; 1269 2; 1270 2; 1271 2; 1272 2; 1273 2; 1274 2; 1275 4; 1276 2; 1277 2; 1278 2; 1279 2; 1280 2; 1281 2; 1282 2; 1283 2; 1284 2; 1285 2; 1286 2; 1287 4; 1288 2; 1289 2; 1290 2; 1291 2; 1292 2; 1293 2; 1294 2; 1295 2; 1296 2; 1297 2; 1298 2; 1299 2; 1300 2; 1301 2; 1302 2; 1303 2; 1304 2; 1305 2; 1306 2; 1307 2; 1308 2; 1309 2; 1310 2; 1311 2; 1312 2; 1313 2; 1314 2; 1315
2; 1316 2; 1317 2; 1318 2; 1319 2; 1320 2; 1321 2; 1322 2; 1323 2; 1324 2; 1325 2; 1326 4; 1327 2; 1328 2; 1329 2; 1330 4; 1331 2; 1332 2; 1333 2; 1334 2; 1335 2; 1336 2;
1337 2; 1338 2; 1339 2; 1340 2; 1341 2; 1342 2; 1343 2; 1344 2; 1345 2; 1346 2; 1347 2; 1348 2; 1349 2; 1350 2; 1351 2; 1352 2; 1353 2; 1354 2; 1355 2; 1356 2; 1357 2; 1358 2; 1359 2; 1360 2; 1361 2; 1362 2; 1363 2; 1364 2; 1365 4; 1366 2; 1367 2; 1368 2; 1369 2; 1370 2; 1371 2; 1372 2; 1373 2; 1374 2; 1375 2; 1376 2; 1377 2; 1378 4; 1379 2; 1380 2; 1381 2; 1382 2; 1383 2; 1384 2; 1385 2; 1386 2; 1387 2; 1388 2; 1389 2; 1390 2; 1391 2; 1392 2; 1393 2; 1394 2; 1395 2; 1396 2; 1397 2; 1398 2; 1399 2; 1400 2; 1401 2; 1402 2; 1403 2; 1404 2; 1405 2; 1406 2; 1407 2; 1408 2; 1409 2; 1410 2; 1411 2; 1412 2; 1413 2; 1414 2; 1415 2; 1416 2; 1417 2; 1418 2; 1419 2; 1420 2; 1421 2; 1422 2; 1423 2; 1424 2; 1425 2; 1426 2; 1427 2; 1428 2; 1429 2; 1430 2; 1431 4; 1432 2; 1433 2; 1434 2; 1435 2; 1436 2; 1437 2; 1438 2; 1439 2; 1440 2; 1441 2; 1442 2; 1443 2; 1444 2; 1445 2; 1446 2; 1447 2; 1448 2; 1449 2; 1450 2; 1451 2; 1452 2; 1453 2; 1454 2; 1455 2; 1456 2; 1457 2; 1458 2; 1459 2; 1460 2; 1461 2; 1462 2; 1463 2; 1464 2; 1465 2; 1466 2; 1467 2; 1468 2; 1469 2; 1470 2; 1471 2; 1472 2; 1473 2; 1474 2; 1475 2; 1476 2; 1477 2; 1478 2; 1479 2; 1480 2; 1481 2; 1482 2; 1483 2; 1484 2; 1485 4; 1486
2; 1487 2; 1488 2; 1489 2; 1490 2; 1491 2; 1492 2; 1493 2; 1494 2; 1495 2; 1496 2; 1497 2; 1498 2; 1499 2; 1500 2; 1501 2; 1502 2; 1503 2; 1504 2; 1505 2; 1506 2; 1507 2;
1508 2; 1509 2; 1510 2; 1511 2; 1512 2; 1513 2; 1514 2; 1515 2; 1516 2; 1517 2; 1518 2; 1519 2; 1520 2; 1521 2; 1522 2; 1523 2; 1524 2; 1525 2; 1526 2; 1527 2; 1528 2; 1529 2; 1530 2; 1531 2; 1532 2; 1533 2; 1534 2; 1535 2; 1536 2; 1537 2; 1538 2; 1539 2; 1540 6; 1541 2; 1542 2; 1543 2; 1544 2; 1545 2; 1546 2; 1547 2; 1548 2; 1549 2; 1550 2; 1551 2; 1552 2; 1553 2; 1554 2; 1555 2; 1556 2; 1557 2; 1558 2; 1559 2; 1560 2; 1561 2; 1562 2; 1563 2; 1564 2; 1565 2; 1566 2; 1567 2; 1568 2; 1569 2; 1570 2; 1571 2; 1572 2; 1573 2; 1574 2; 1575 2; 1576 2; 1577 2; 1578 2; 1579 2; 1580 2; 1581 2; 1582 2; 1583 2; 1584 2; 1585 2; 1586 2; 1587 2; 1588 2; 1589 2; 1590 2; 1591 2; 1592 2; 1593 2; 1594 2; 1595 2; 1596 4; 1597 2; 1598 2; 1599 2; 1600 2; 1601 2; 1602 2; 1603 2; 1604 2; 1605 2; 1606 2; 1607 2; 1608 2; 1609 2; 1610 2; 1611 2; 1612 2; 1613 2; 1614 2; 1615 2; 1616 2; 1617 2; 1618 2; 1619 2; 1620 2; 1621 2; 1622 2; 1623 2; 1624 2; 1625 2; 1626 2; 1627 2; 1628 2; 1629 2; 1630 2; 1631 2; 1632 2; 1633 2; 1634 2; 1635 2; 1636 2; 1637 2; 1638 2; 1639 2; 1640 2; 1641 2; 1642 2; 1643 2; 1644 2; 1645 2; 1646 2; 1647 2; 1648 2; 1649 2; 1650 2; 1651 2; 1652 2; 1653 4; 1654 2; 1655 2; 1656 2; 1657
2; 1658 2; 1659 2; 1660 2; 1661 2; 1662 2; 1663 2; 1664 2; 1665 2; 1666 2; 1667 2; 1668 2; 1669 2; 1670 2; 1671 2; 1672 2; 1673 2; 1674 2; 1675 2; 1676 2; 1677 2; 1678 2;
1679 2; 1680 2; 1681 2; 1682 2; 1683 2; 1684 2; 1685 2; 1686 2; 1687 2; 1688 2; 1689 2; 1690 2; 1691 2; 1692 2; 1693 2; 1694 2; 1695 2; 1696 2; 1697 2; 1698 2; 1699 2; 1700 2; 1701 2; 1702 2; 1703 2; 1704 2; 1705 2; 1706 2; 1707 2; 1708 2; 1709 2; 1710 2; 1711 4; 1712 2; 1713 2; 1714 2; 1715 2; 1716 4; 1717 2; 1718 2; 1719 2; 1720 2; 1721 2; 1722 2; 1723 2; 1724 2; 1725 2; 1726 2; 1727 2; 1728 2; 1729 2; 1730 2; 1731 2; 1732 2; 1733 2; 1734 2; 1735 2; 1736 2; 1737 2; 1738 2; 1739 2; 1740 2; 1741 2; 1742 2; 1743 2; 1744 2; 1745 2; 1746 2; 1747 2; 1748 2; 1749 2; 1750 2; 1751 2; 1752 2; 1753 2; 1754 2; 1755 2; 1756 2; 1757 2; 1758 2; 1759 2; 1760 2; 1761 2; 1762 2; 1763 2; 1764 2; 1765 2; 1766 2; 1767 2; 1768 2; 1769 2; 1770 4; 1771 4; 1772 2; 1773 2; 1774 2; 1775 2; 1776 2; 1777 2; 1778 2; 1779 2; 1780 2; 1781 2; 1782 2; 1783 2; 1784 2; 1785 2; 1786 2; 1787 2; 1788 2; 1789 2; 1790 2; 1791 2; 1792 2; 1793 2; 1794 2; 1795 2; 1796 2; 1797 2; 1798 2; 1799 2; 1800 2; 1801 2; 1802 2; 1803 2; 1804 2; 1805 2; 1806 2; 1807 2; 1808 2; 1809 2; 1810 2; 1811 2; 1812 2; 1813 2; 1814 2; 1815 2; 1816 2; 1817 2; 1818 2; 1819 2; 1820 4; 1821 2; 1822 2; 1823 2; 1824 2; 1825 2; 1826 2; 1827 2; 1828
2; 1829 2; 1830 4; 1831 2; 1832 2; 1833 2; 1834 2; 1835 2; 1836 2; 1837 2; 1838 2; 1839 2; 1840 2; 1841 2; 1842 2; 1843 2; 1844 2; 1845 2; 1846 2; 1847 2; 1848 2; 1849 2;
1850 2; 1851 2; 1852 2; 1853 2; 1854 2; 1855 2; 1856 2; 1857 2; 1858 2; 1859 2; 1860 2; 1861 2; 1862 2; 1863 2; 1864 2; 1865 2; 1866 2; 1867 2; 1868 2; 1869 2; 1870 2; 1871 2; 1872 2; 1873 2; 1874 2; 1875 2; 1876 2; 1877 2; 1878 2; 1879 2; 1880 2; 1881 2; 1882 2; 1883 2; 1884 2; 1885 2; 1886 2; 1887 2; 1888 2; 1889 2; 1890 2; 1891 4; 1892 2; 1893 2; 1894 2; 1895 2; 1896 2; 1897 2; 1898 2; 1899 2; 1900 2; 1901 2; 1902 2; 1903 2; 1904 2; 1905 2; 1906 2; 1907 2; 1908 2; 1909 2; 1910 2; 1911 2; 1912 2; 1913 2; 1914 2; 1915 2; 1916 2; 1917 2; 1918 2; 1919 2; 1920 2; 1921 2; 1922 2; 1923 2; 1924 2; 1925 2; 1926 2; 1927 2; 1928 2; 1929 2; 1930 2; 1931 2; 1932 2; 1933 2; 1934 2; 1935 2; 1936 2; 1937 2; 1938 2; 1939 2; 1940 2; 1941 2; 1942 2; 1943 2; 1944 2; 1945 2; 1946 2; 1947 2; 1948 2; 1949 2; 1950 2; 1951 2; 1952 2; 1953 4; 1954 2; 1955 2; 1956 2; 1957 2; 1958 2; 1959 2; 1960 2; 1961 2; 1962 2; 1963 2; 1964 2; 1965 2; 1966 2; 1967 2; 1968 2; 1969 2; 1970 2; 1971 2; 1972 2; 1973 2; 1974 2; 1975 2; 1976 2; 1977 2; 1978 2; 1979 2; 1980 2; 1981 2; 1982 2; 1983 2; 1984 2; 1985 2; 1986 2; 1987 2; 1988 2; 1989 2; 1990 2; 1991 2; 1992 2; 1993 2; 1994 2; 1995 2; 1996 2; 1997 2; 1998 2; 1999
2; 2000 2; 2001 2; 2002 4; 2003 2; 2004 2; 2005 2; 2006 2; 2007 2; 2008 2; 2009 2; 2010 2; 2011 2; 2012 2; 2013 2; 2014 2; 2015 2; 2016 4; 2017 2; 2018 2; 2019 2; 2020 2;
2021 2; 2022 2; 2023 2; 2024 4; 2025 2; 2026 2; 2027 2; 2028 2; 2029 2; 2030 2; 2031 2; 2032 2; 2033 2; 2034 2; 2035 2; 2036 2; 2037 2; 2038 2; 2039 2; 2040 2; 2041 2; 2042 2; 2043 2; 2044 2; 2045 2; 2046 2; 2047 2; 2048 2; 2049 2; 2050 2; 2051 2; 2052 2; 2053 2; 2054 2; 2055 2; 2056 2; 2057 2; 2058 2; 2059 2; 2060 2; 2061 2; 2062 2; 2063 2; 2064 2; 2065 2; 2066 2; 2067 2; 2068 2; 2069 2; 2070 2; 2071 2; 2072 2; 2073 2; 2074 2; 2075 2; 2076 2; 2077 2; 2078 2; 2079 2; 2080 4; 2081 2; 2082 2; 2083 2; 2084 2; 2085 2; 2086 2; 2087 2; 2088 2; 2089 2; 2090 2; 2091 2; 2092 2; 2093 2; 2094 2; 2095 2; 2096 2; 2097 2; 2098 2; 2099 2; 2100 2; 2101 2; 2102 2; 2103 2; 2104 2; 2105 2; 2106 2; 2107 2; 2108 2; 2109 2; 2110 2; 2111 2; 2112 2; 2113 2; 2114 2; 2115 2; 2116 2; 2117 2; 2118 2; 2119 2; 2120 2; 2121 2; 2122 2; 2123 2; 2124 2; 2125 2; 2126 2; 2127 2; 2128 2; 2129 2; 2130 2; 2131 2; 2132 2; 2133 2; 2134 2; 2135 2; 2136 2; 2137 2; 2138 2; 2139 2; 2140 2; 2141 2; 2142 2; 2143 2; 2144 2; 2145 4; 2146 2; 2147 2; 2148 2; 2149 2; 2150 2; 2151 2; 2152 2; 2153 2; 2154 2; 2155 2; 2156 2; 2157 2; 2158 2; 2159 2; 2160 2; 2161 2; 2162 2; 2163 2; 2164 2; 2165 2; 2166 2; 2167 2; 2168 2; 2169 2; 2170
2; 2171 2; 2172 2; 2173 2; 2174 2; 2175 2; 2176 2; 2177 2; 2178 2; 2179 2; 2180 2; 2181 2; 2182 2; 2183 2; 2184 2; 2185 2; 2186 2; 2187 2; 2188 2; 2189 2; 2190 2; 2191 2;
2192 2; 2193 2; 2194 2; 2195 2; 2196 2; 2197 2; 2198 2; 2199 2; 2200 2; 2201 2; 2202 2; 2203 2; 2204 2; 2205 2; 2206 2; 2207 2; 2208 2; 2209 2; 2210 2; 2211 4; 2212 2; 2213 2; 2214 2; 2215 2; 2216 2; 2217 2; 2218 2; 2219 2; 2220 2; 2221 2; 2222 2; 2223 2; 2224 2; 2225 2; 2226 2; 2227 2; 2228 2; 2229 2; 2230 2; 2231 2; 2232 2; 2233 2; 2234 2; 2235 2; 2236 2; 2237 2; 2238 2; 2239 2; 2240 2; 2241 2; 2242 2; 2243 2; 2244 2; 2245 2; 2246 2; 2247 2; 2248 2; 2249 2; 2250 2; 2251 2; 2252 2; 2253 2; 2254 2; 2255 2; 2256 2; 2257 2; 2258 2; 2259 2; 2260 2; 2261 2; 2262 2; 2263 2; 2264 2; 2265 2; 2266 2; 2267 2; 2268 2; 2269 2; 2270 2; 2271 2; 2272 2; 2273 2; 2274 2; 2275 2; 2276 2; 2277 2; 2278 4; 2279 2; 2280 2; 2281 2; 2282 2; 2283 2; 2284 2; 2285 2; 2286 2; 2287 2; 2288 2; 2289 2; 2290 2; 2291 2; 2292 2; 2293 2; 2294 2; 2295 2; 2296 2; 2297 2; 2298 2; 2299 2; 2300 4; 2301 2; 2302 2; 2303 2; 2304 2; 2305 2; 2306 2; 2307 2; 2308 2; 2309 2; 2310 2; 2311 2; 2312 2; 2313 2; 2314 2; 2315 2; 2316 2; 2317 2; 2318 2; 2319 2; 2320 2; 2321 2; 2322 2; 2323 2; 2324 2; 2325 2; 2326 2; 2327 2; 2328 2; 2329 2; 2330 2; 2331 2; 2332 2; 2333 2; 2334 2; 2335 2; 2336 2; 2337 2; 2338 2; 2339 2; 2340 2; 2341
2; 2342 2; 2343 2; 2344 2; 2345 2; 2346 4; 2347 2; 2348 2; 2349 2; 2350 2; 2351 2; 2352 2; 2353 2; 2354 2; 2355 2; 2356 2; 2357 2; 2358 2; 2359 2; 2360 2; 2361 2; 2362 2;
2363 2; 2364 2; 2365 2; 2366 2; 2367 2; 2368 2; 2369 2; 2370 2; 2371 2; 2372 2; 2373 2; 2374 2; 2375 2; 2376 2; 2377 2; 2378 2; 2379 2; 2380 4; 2381 2; 2382 2; 2383 2; 2384 2; 2385 2; 2386 2; 2387 2; 2388 2; 2389 2; 2390 2; 2391 2; 2392 2; 2393 2; 2394 2; 2395 2; 2396 2; 2397 2; 2398 2; 2399 2; 2400 2; 2401 2; 2402 2; 2403 2; 2404 2; 2405 2; 2406 2; 2407 2; 2408 2; 2409 2; 2410 2; 2411 2; 2412 2; 2413 2; 2414 2; 2415 4; 2416 2; 2417 2; 2418 2; 2419 2; 2420 2; 2421 2; 2422 2; 2423 2; 2424 2; 2425 2; 2426 2; 2427 2; 2428 2; 2429 2; 2430 2; 2431 2; 2432 2; 2433 2; 2434 2; 2435 2; 2436 2; 2437 2; 2438 2; 2439 2; 2440 2; 2441 2; 2442 2; 2443 2; 2444 2; 2445 2; 2446 2; 2447 2; 2448 2; 2449 2; 2450 2; 2451 2; 2452 2; 2453 2; 2454 2; 2455 2; 2456 2; 2457 2; 2458 2; 2459 2; 2460 2; 2461 2; 2462 2; 2463 2; 2464 2; 2465 2; 2466 2; 2467 2; 2468 2; 2469 2; 2470 2; 2471 2; 2472 2; 2473 2; 2474 2; 2475 2; 2476 2; 2477 2; 2478 2; 2479 2; 2480 2; 2481 2; 2482 2; 2483 2; 2484 2; 2485 4; 2486 2; 2487 2; 2488 2; 2489 2; 2490 2; 2491 2; 2492 2; 2493 2; 2494 2; 2495 2; 2496 2; 2497 2; 2498 2; 2499 2; 2500 2; 2501 2; 2502 2; 2503 2; 2504 2; 2505 2; 2506 2; 2507 2; 2508 2; 2509 2; 2510 2; 2511 2; 2512
2; 2513 2; 2514 2; 2515 2; 2516 2; 2517 2; 2518 2; 2519 2; 2520 2; 2521 2; 2522 2; 2523 2; 2524 2; 2525 2; 2526 2; 2527 2; 2528 2; 2529 2; 2530 2; 2531 2; 2532 2; 2533 2;
2534 2; 2535 2; 2536 2; 2537 2; 2538 2; 2539 2; 2540 2; 2541 2; 2542 2; 2543 2; 2544 2; 2545 2; 2546 2; 2547 2; 2548 2; 2549 2; 2550 2; 2551 2; 2552 2; 2553 2; 2554 2; 2555 2; 2556 4; 2557 2; 2558 2; 2559 2; 2560 2; 2561 2; 2562 2; 2563 2; 2564 2; 2565 2; 2566 2; 2567 2; 2568 2; 2569 2; 2570 2; 2571 2; 2572 2; 2573 2; 2574 2; 2575 2; 2576 2; 2577 2; 2578 2; 2579 2; 2580 2; 2581 2; 2582 2; 2583 2; 2584 2; 2585 2; 2586 2; 2587 2; 2588 2; 2589 2; 2590 2; 2591 2; 2592 2; 2593 2; 2594 2; 2595 2; 2596 2; 2597 2; 2598 2; 2599 2; 2600 4; 2601 2; 2602 2; 2603 2; 2604 2; 2605 2; 2606 2; 2607 2; 2608 2; 2609 2; 2610 2; 2611 2; 2612 2; 2613 2; 2614 2; 2615 2; 2616 2; 2617 2; 2618 2; 2619 2; 2620 2; 2621 2; 2622 2; 2623 2; 2624 2; 2625 2; 2626 2; 2627 2; 2628 4; 2629 2; 2630 2; 2631 2; 2632 2; 2633 2; 2634 2; 2635 2; 2636 2; 2637 2; 2638 2; 2639 2; 2640 2; 2641 2; 2642 2; 2643 2; 2644 2; 2645 2; 2646 2; 2647 2; 2648 2; 2649 2; 2650 2; 2651 2; 2652 2; 2653 2; 2654 2; 2655 2; 2656 2; 2657 2; 2658 2; 2659 2; 2660 2; 2661 2; 2662 2; 2663 2; 2664 2; 2665 2; 2666 2; 2667 2; 2668 2; 2669 2; 2670 2; 2671 2; 2672 2; 2673 2; 2674 2; 2675 2; 2676 2; 2677 2; 2678 2; 2679 2; 2680 2; 2681 2; 2682 2; 2683
2; 2684 2; 2685 2; 2686 2; 2687 2; 2688 2; 2689 2; 2690 2; 2691 2; 2692 2; 2693 2; 2694 2; 2695 2; 2696 2; 2697 2; 2698 2; 2699 2; 2700 2; 2701 4; 2702 2; 2703 2; 2704 2;
2705 2; 2706 2; 2707 2; 2708 2; 2709 2; 2710 2; 2711 2; 2712 2; 2713 2; 2714 2; 2715 2; 2716 2; 2717 2; 2718 2; 2719 2; 2720 2; 2721 2; 2722 2; 2723 2; 2724 2; 2725 2; 2726 2; 2727 2; 2728 2; 2729 2; 2730 2; 2731 2; 2732 2; 2733 2; 2734 2; 2735 2; 2736 2; 2737 2; 2738 2; 2739 2; 2740 2; 2741 2; 2742 2; 2743 2; 2744 2; 2745 2; 2746 2; 2747 2; 2748 2; 2749 2; 2750 2; 2751 2; 2752 2; 2753 2; 2754 2; 2755 2; 2756 2; 2757 2; 2758 2; 2759 2; 2760 2; 2761 2; 2762 2; 2763 2; 2764 2; 2765 2; 2766 2; 2767 2; 2768 2; 2769 2; 2770 2; 2771 2; 2772 2; 2773 2; 2774 2; 2775 4; 2776 2; 2777 2; 2778 2; 2779 2; 2780 2; 2781 2; 2782 2; 2783 2; 2784 2; 2785 2; 2786 2; 2787 2; 2788 2; 2789 2; 2790 2; 2791 2; 2792 2; 2793 2; 2794 2; 2795 2; 2796 2; 2797 2; 2798 2; 2799 2; 2800 2; 2801 2; 2802 2; 2803 2; 2804 2; 2805 2; 2806 2; 2807 2; 2808 2; 2809 2; 2810 2; 2811 2; 2812 2; 2813 2; 2814 2; 2815 2; 2816 2; 2817 2; 2818 2; 2819 2; 2820 2; 2821 2; 2822 2; 2823 2; 2824 2; 2825 2; 2826 2; 2827 2; 2828 2; 2829 2; 2830 2; 2831 2; 2832 2; 2833 2; 2834 2; 2835 2; 2836 2; 2837 2; 2838 2; 2839 2; 2840 2; 2841 2; 2842 2; 2843 2; 2844 2; 2845 2; 2846 2; 2847 2; 2848 2; 2849 2; 2850 4; 2851 2; 2852 2; 2853 2; 2854
2; 2855 2; 2856 2; 2857 2; 2858 2; 2859 2; 2860 2; 2861 2; 2862 2; 2863 2; 2864 2; 2865 2; 2866 2; 2867 2; 2868 2; 2869 2; 2870 2; 2871 2; 2872 2; 2873 2; 2874 2; 2875 2;
2876 2; 2877 2; 2878 2; 2879 2; 2880 2; 2881 2; 2882 2; 2883 2; 2884 2; 2885 2; 2886 2; 2887 2; 2888 2; 2889 2; 2890 2; 2891 2; 2892 2; 2893 2; 2894 2; 2895 2; 2896 2; 2897 2; 2898 2; 2899 2; 2900 2; 2901 2; 2902 2; 2903 2; 2904 2; 2905 2; 2906 2; 2907 2; 2908 2; 2909 2; 2910 2; 2911 2; 2912 2; 2913 2; 2914 2; 2915 2; 2916 2; 2917 2; 2918 2; 2919 2; 2920 2; 2921 2; 2922 2; 2923 2; 2924 2; 2925 4; 2926 4; 2927 2; 2928 2; 2929 2; 2930 2; 2931 2; 2932 2; 2933 2; 2934 2; 2935 2; 2936 2; 2937 2; 2938 2; 2939 2; 2940 2; 2941 2; 2942 2; 2943 2; 2944 2; 2945 2; 2946 2; 2947 2; 2948 2; 2949 2; 2950 2; 2951 2; 2952 2; 2953 2; 2954 2; 2955 2; 2956 2; 2957 2; 2958 2; 2959 2; 2960 2; 2961 2; 2962 2; 2963 2; 2964 2; 2965 2; 2966 2; 2967 2; 2968 2; 2969 2; 2970 2; 2971 2; 2972 2; 2973 2; 2974 2; 2975 2; 2976 2; 2977 2; 2978 2; 2979 2; 2980 2; 2981 2; 2982 2; 2983 2; 2984 2; 2985 2; 2986 2; 2987 2; 2988 2; 2989 2; 2990 2; 2991 2; 2992 2; 2993 2; 2994 2; 2995 2; 2996 2; 2997 2; 2998 2; 2999 2; 3000 2; 3001 2; 3002 2; 3003 8; 3060 2; 3081 2; 3160 2; 3240 2; 3276 2; 3321 2; 3403 2; 3432 1; 3486 2; 3570 2; 3654 2; 3655 2; 3741 2; 3828 2; 3876 2; 3916 2; 4005 2; 4060 2; 4095 2; 4186 2; 4278 2; 4368
2; 4371 2; 4465 2; 4495 2; 4560 2; 4656 2; 4753 2; 4845 2; 4851 2; 4950 2; 4960 2; 5005 2; 5050 2; 5151 2; 5253 2; 5356 2; 5456 2; 5460 2; 5565 2; 5671 2; 5778 2; 5886 2;
5984 2; 5985 2; 5995 2; 6105 2; 6188 2; 6216 2; 6328 2; 6435 2; 6441 2; 6545 2; 6555 2; 6670 2; 6786 2; 6903 2; 7021 2; 7140 4; 7260 2; 7315 2; 7381 2; 7503 2; 7626 2; 7750 2; 7770 2; 7875 2; 8001 2; 8008 2; 8128 2; 8256 2; 8385 2; 8436 2; 8515 2; 8568 2; 8646 2; 8778 2; 8855 2; 8911 2; 9045 2; 9139 2; 9180 2; 9316 2; 9453 2; 9591 2; 9730 2; 9870 2; 9880 2; 10011 2; 10153 2; 10296 2; 10440 2; 10585 2; 10626 2; 10660 2; 10731 2; 10878 2; 11026 2; 11175 2; 11325 2; 11440 2; 11476 2; 11480 2; 11628 4; 11781 2;
11935 2; 12090 2; 12246 2; 12341 2; 12376 2; 12403 2; 12561 2; 12650 2; 12720 2; 12870 1; 12880 2; 13041 2; 13203 2; 13244 2; 13366 2; 13530 2; 13695 2; 13861 2; 14028 2;
14190 2; 14196 2; 14365 2; 14535 2; 14706 2; 14878 2; 14950 2; 15051 2; 15180 2; 15225 2; 15400 2; 15504 2; 15576 2; 15753 2; 15931 2; 16110 2; 16215 2; 16290 2; 16471 2;
16653 2; 16836 2; 17020 2; 17205 2; 17296 2; 17391 2; 17550 2; 17578 2; 17766 2; 17955 2; 18145 2; 18336 2; 18424 2; 18528 2; 18564 2; 18721 2; 18915 2; 19110 2; 19306 2;
19448 2; 19503 2; 19600 2; 19701 2; 19900 2; 20100 2; 20301 2; 20349 2; 20475 2; 20503 2; 20706 2; 20825 2; 20910 2; 21115 2; 21321 2; 21528 2; 21736 2; 21945 2; 22100 2;
22155 2; 22366 2; 22578 2; 22791 2; 23005 2; 23220 2; 23426 2; 23436 2; 23653 2; 23751 2; 23871 2; 24090 2; 24310 4; 24531 2; 24753 2; 24804 2; 24976 2; 25200 2; 25425 2;
25651 2; 25878 2; 26106 2; 26235 2; 26334 2; 26335 2; 26565 2; 26796 2; 27028 2; 27132 2; 27261 2; 27405 2; 27495 2; 27720 2; 27730 2; 27966 2; 28203 2; 28441 2; 28680 2;
28920 2; 29161 2; 29260 2; 29403 2; 29646 2; 29890 2; 30135 2; 30381 2; 30628 2; 30856 2; 30876 2; 31125 2; 31375 2; 31465 2; 31626 2; 31824 2; 31878 2; 32131 2; 32385 2;
32509 2; 32640 2; 32896 2; 33153 2; 33411 2; 33649 2; 33670 2; 33930 2; 34191 2; 34220 2; 34453 2; 34716 2; 34980 2; 35245 2; 35511 2; 35778 2; 35960 2; 35990 2; 36046 2;
36315 2; 36585 2; 36856 2; 37128 2; 37401 2; 37675 2; 37820 2; 37950 2; 38226 2; 38503 2; 38760 2; 38781 2; 39060 2; 39340 2; 39621 2; 39711 2; 39903 2; 40186 2; 40470 2;
40755 2; 40920 2; 41041 2; 41328 2; 41616 2; 41664 2; 41905 2; 42195 2; 42486 2; 42504 2; 42778 2; 43071 2; 43365 2; 43660 2; 43680 2; 43758 2; 43956 2; 44253 2; 44551 2;
44850 2; 45150 2; 45451 2; 45753 2; 45760 2; 46056 2; 46360 2; 46376 2; 46665 2; 46971 2; 47278 2; 47586 2; 47895 2; 47905 2; 48205 2; 48516 2; 48620 1; 48828 2; 49141 2;
49455 2; 49770 2; 50086 2; 50116 2; 50388 2; 50403 2; 50721 2; 51040 2; 51360 2; 51681 2; 52003 2; 52326 2; 52360 2; 52394 2; 52650 2; 52975 2; 53130 2; 53301 2; 53628 2;
53956 2; 54264 2; 54285 2; 54615 2; 54740 2; 54946 2; 55278 2; 55611 2; 55945 2; 56280 2; 56616 2; 56953 2; 57155 2; 57291 2; 57630 2; 57970 2; 58311 2; 58653 2; 58905 2;
58996 2; 59340 2; 59640 2; 59685 2; 60031 2; 60378 2; 60726 2; 61075 2; 61425 2; 61776 2; 62128 2; 62196 2; 62481 2; 62835 2; 63190 2; 63546 2; 63903 2; 64261 2; 64620 2;
64824 2; 64980 2; 65341 2; 65703 2; 65780 2; 66045 2; 66066 2; 66430 2; 66795 2; 67161 2; 67525 2; 67528 2; 67896 2; 68265 2; 68635 2; 69006 2; 69378 2; 69751 2; 70125 2;
70300 2; 70500 2; 70876 2; 71253 2; 71631 2; 72010 2; 72390 2; 72771 2; 73150 2; 73153 2; 73536 2; 73815 2; 73920 2; 74305 2; 74613 2; 74691 2; 75078 2; 75466 2; 75582 2;
75855 2; 76076 2; 76245 2; 76636 2; 77028 2; 77421 2; 77520 2; 77815 2; 78210 2; 78606 2; 79003 2; 79079 2; 79401 2; 79800 2; 80200 2; 80601 2; 80730 2; 81003 2; 81406 2;
81810 2; 82160 2; 82215 2; 82251 2; 82621 2; 83028 2; 83436 2; 83845 2; 84255 2; 84666 2; 85078 2; 85320 2; 85491 2; 85905 2; 86320 2; 86736 2; 87153 2; 87571 2; 87990 2;
88410 2; 88560 2; 88831 2; 89253 2; 89676 2; 90100 2; 90525 2; 90951 2; 91378 2; 91390 2; 91806 2; 91881 2; 92235 2; 92378 2; 92665 2; 93096 2; 93528 2; 93961 2; 94395 2;
94830 2; 95266 2; 95284 2; 95703 2; 96141 2; 96580 2; 97020 2; 97461 2; 97903 2; 98280 2; 98346 2; 98770 2; 98790 2; 99235 2; 99681 2; 100128 2; 100576 2; 100947 2; 101025 2; 101270 2; 101475 2; 101926 2; 102340 2; 102378 2; 102831 2; 103285 2; 103740 2; 104196 2; 104653 2; 105111 2; 105570 2; 105995 2; 106030 2; 106491 2; 106953 2; 107416
2; 107880 2; 108345 2; 108811 2; 109278 2; 109736 2; 109746 2; 110215 2; 110685 2; 111156 2; 111628 2; 111930 2; 112101 2; 112575 2; 113050 2; 113526 2; 113564 2; 114003 2; 114481 2; 114960 2; 115440 2; 115921 2; 116280 2; 116403 2; 116886 2; 117370 2; 117480 2; 117855 2; 118341 2; 118755 2; 118828 2; 119316 2; 119805 2; 120295 2; 120786 2; 121278 2; 121485 2; 121771 2; 122265 2; 122760 2; 123256 2; 123410 2; 123753 2; 124251 2; 124750 2; 125250 2; 125580 2; 125751 2; 125970 2; 126253 2; 126756 2; 127260 2;
127765 2; 128271 2; 128778 2; 129286 2; 129766 2; 129795 2; 130305 2; 130816 2; 131328 2; 131841 2; 132355 2; 132870 2; 133386 2; 133903 2; 134044 2; 134421 2; 134596 2; 134940 2; 135460 2; 135751 2; 135981 2; 136503 2; 137026 2; 137550 2; 138075 2; 138415 2; 138601 2; 139128 2; 139656 2; 140185 2; 140715 2; 141246 2; 141778 2; 142311 2; 142506 2; 142845 2; 142880 2; 143380 2; 143916 2; 144453 2; 144991 2; 145530 2; 146070 2; 146611 2; 147153 2; 147440 2; 147696 2; 148240 2; 148785 2; 148995 2; 149331 2; 149878 2; 150426 2; 150975 2; 151525 2; 152076 2; 152096 2; 152628 2; 153181 2; 153735 2; 154290 2; 154846 2; 155403 2; 155961 2; 156520 2; 156849 2; 157080 2; 157641 2; 158203 2; 158766 2; 159330 2; 159895 2; 160461 2; 161028 2; 161596 2; 161700 2; 162165 2; 162735 2; 163185 2; 163306 2; 163878 2; 164451 2; 165025 2; 165600 2; 166176 2; 166650 2; 166753 2; 167331 2; 167910 2; 167960 2; 168490 2; 169071 2; 169653 2; 169911 2; 170236 2; 170544 2; 170820 2; 171405 2; 171700 2; 171991 2; 172578 2; 173166 2; 173755 2; 174345 2; 174936 2; 175528 2; 176121 2; 176715 2; 176851 2; 177100 2; 177310 2; 177906 2; 178365 2; 178503 2; 179101 2; 179700 2; 180300 2; 180901 2; 181503 2; 182104
2; 182106 2; 182710 2; 183315 2; 183921 2; 184528 2; 184756 1; 185136 2; 185745 2; 186355 2; 186966 2; 187460 2; 187578 2; 188191 2; 188805 2; 189420 2; 190036 2; 190653 2; 191271 2; 191890 2; 192510 2; 192920 2; 193131 2; 193753 2; 194376 2; 194580 2; 195000 2; 195625 2; 196251 2; 196878 2; 197506 2; 198135 2; 198485 2; 198765 2; 199396 2; 200028 2; 200661 2; 201295 2; 201376 2; 201930 2; 202566 2; 203203 2; 203490 2; 203841 2; 204156 2; 204480 2; 205120 2; 205761 2; 206403 2; 207046 2; 207690 2; 208335 2;
208981 2; 209628 2; 209934 2; 210276 2; 210925 2; 211575 2; 211876 2; 212226 2; 212878 2; 213531 2; 214185 2; 214840 2; 215496 2; 215820 2; 216153 2; 216811 2; 217470 2; 218130 2; 218791 2; 219453 2; 220116 2; 220780 2; 221445 2; 221815 2; 222111 2; 222778 2; 223446 2; 224115 2; 224785 2; 225456 2; 226128 2; 226801 2; 227475 2; 227920 2; 228150 2; 228826 2; 229503 2; 230181 2; 230230 2; 230300 2; 230860 2; 231540 2; 232221 2; 232903 2; 233586 2; 234136 2; 234270 2; 234955 2; 235641 2; 236328 2; 237016 2; 237336 2; 237705 2; 238395 2; 239086 2; 239778 2; 240464 2; 240471 2; 241165 2; 241860 2; 242556 2; 243253 2; 243951 2; 244650 2; 245157 2; 245350 2; 246051 2; 246753 2; 246905 2; 247456 2; 248160 2; 248865 2; 249571 2; 249900 2; 250278 2; 250986 2; 251695 2; 252405 2; 253116 2; 253460 2; 253828 2; 254541 2; 255255 2; 255970 2; 256686 2; 257403 2; 258121 2; 258840 2; 259560 2; 260130 2; 260281 2; 261003 2; 261726 2; 262450 2; 263175 2; 263901 2; 264628 2; 265356 2; 266085 2; 266815 2; 266916 2; 267546 2; 268278 2; 269011 2; 269745 2; 270480 2; 270725 2; 271216 2; 271953 2; 272691 2; 273430 2; 273819 2; 274170 2; 274911 2; 275653 2; 276396 2; 277140 2; 277885 2; 278256 2; 278631
2; 279378 2; 280126 2; 280840 2; 280875 2; 281625 2; 282376 2; 283128 2; 283881 2; 284635 2; 285390 2; 286146 2; 286903 2; 287661 2; 287980 2; 288420 2; 289180 2; 289941 2; 290703 2; 291466 2; 292230 2; 292825 2; 292995 2; 293761 2; 293930 2; 294528 2; 295240 2; 295296 2; 296010 2; 296065 2; 296835 2; 297606 2; 298378 2; 299151 2; 299925 2; 300700 2; 301476 2; 302253 2; 302621 2; 303031 2; 303810 2; 304590 2; 305371 2; 306153 2; 306936 2; 307720 2; 308505 2; 309291 2; 310078 2; 310124 2; 310866 2; 311655 2;
312445 2; 313236 2; 314028 2; 314821 2; 315615 2; 316251 2; 316410 2; 317206 2; 317750 2; 318003 2; 318801 2; 319600 2; 319770 2; 320400 2; 321201 2; 322003 2; 322806 2; 323610 2; 324415 2; 324632 2; 325221 2; 325500 2; 326028 2; 326836 2; 327645 2; 328455 2; 329266 2; 330078 2; 330891 2; 331705 2; 332520 2; 333336 2; 333375 2; 334153 2; 334971 2; 335790 2; 336610 2; 337431 2; 338253 2; 339076 2; 339900 2; 340725 2; 341055 2; 341376 2; 341551 2; 342378 2; 343206 2; 344035 2; 344865 2; 345696 2; 346104 2; 346528 2; 347361 2; 348195 2; 349030 2; 349504 2; 349866 2; 350703 2; 351541 2; 352380 2; 352716 2; 353220 2; 354061 2; 354903 2; 355746 2; 356590 2; 357435 2; 357760 2; 358281 2; 359128 2; 359976 2; 360825 2; 361675 2; 362526 2; 363378 2; 364231 2; 365085 2; 365940 2; 366145 2; 366796 2; 367290 2; 367653 2; 368511 2; 369370 2; 370230 2; 371091 2; 371953 2; 372816 2; 373680 2; 374545 2; 374660 2; 375411 2; 376278 2; 376740 2; 376992 2; 377146 2; 378015 2; 378885 2; 379756 2; 380628 2; 381501 2; 382375 2; 383250 2; 383306 2; 384126 2; 385003 2; 385881 2; 386760 2; 387640 2; 388521 2; 389403 2; 390286 2; 391170 2; 392055 2; 392084 2; 392941 2; 393828 2; 394716 2; 395010 2; 395605
2; 396495 2; 397386 2; 398278 2; 399171 2; 400065 2; 400960 2; 400995 2; 401856 2; 402753 2; 403651 2; 404550 2; 405450 2; 406351 2; 407253 2; 408156 2; 409060 2; 409965 2; 410040 2; 410871 2; 411778 2; 412686 2; 413595 2; 414505 2; 415416 2; 416328 2; 417241 2; 418155 2; 419070 2; 419220 2; 419986 2; 420903 2; 421821 2; 422740 2; 423660 2; 424270 2; 424581 2; 425503 2; 426426 2; 427350 2; 428275 2; 428536 2; 429201 2; 430128 2; 431056 2; 431985 2; 432915 2; 433846 2; 434778 2; 435711 2; 435897 2; 436645 2;
437580 2; 437989 2; 438516 2; 439453 2; 440391 2; 441330 2; 442270 2; 443211 2; 444153 2; 445096 2; 446040 2; 446985 2; 447580 2; 447931 2; 448878 2; 449826 2; 450775 2; 451725 2; 452676 2; 453628 2; 454581 2; 455126 2; 455535 2; 456490 2; 457310 2; 457446 2; 458403 2; 459361 2; 460320 2; 461280 2; 462241 2; 463203 2; 464166 2; 465130 2; 466095 2; 467061 2; 467180 2; 468028 2; 468996 2; 469965 2; 470935 2; 471906 2; 472878 2; 473851 2; 474825 2; 475020 2; 475800 2; 476776 2; 477191 2; 477753 2; 478731 2; 479710 2; 480690 2; 480700 2; 481671 2; 482653 2; 483636 2; 484620 2; 485605 2; 486591 2; 487344 2; 487578 2; 487635 2; 488566 2; 489555 2; 490314 2; 490545 2; 491536 2; 492528 2; 493521 2; 494515 2; 495510 2; 496506 2; 497420 2; 497503 2; 497640 2; 498501 2; 499500 2; 500500 2; 501501 2; 501942 2; 502503 2; 503506 2; 504510 2; 505515 2; 506521 2; 507528 2; 508080 2; 508536 2; 509545 2; 510555 2; 511566 2; 512578 2; 513591 2; 514605 2; 515620 2; 516636 2; 517653 2; 518665 2; 518671 2; 519690 2; 520710 2; 521731 2; 521855 2; 522753 2; 523776 2; 524800 2; 525825 2; 526851 2; 527878 2; 528906 2; 529396 2; 529935 2; 530965 2; 531996 2; 533028 2; 534061 2; 535095 2; 536130 2; 537166
2; 538203 2; 539241 2; 540274 2; 540280 2; 541320 2; 542361 2; 543403 2; 544446 2; 545490 2; 546535 2; 547581 2; 548628 2; 549676 2; 550725 2; 551300 2; 551775 2; 552826 2; 553878 2; 554931 2; 555985 2; 557040 2; 557845 2; 558096 2; 559153 2; 560211 2; 561270 2; 562330 2; 562475 2; 563391 2; 564453 2; 565516 2; 566580 2; 567645 2; 568711 2; 569778 2; 570846 2; 571915 2; 572985 2; 573800 2; 574056 2; 575128 2; 575757 2; 576201 2; 577275 2; 578350 2; 579426 2; 580503 2; 581581 2; 582660 2; 583740 2; 584821 2;
585276 2; 585903 2; 586986 2; 588070 2; 589155 2; 590241 2; 591328 2; 592416 2; 593505 2; 593775 2; 594595 2; 595665 2; 595686 2; 596778 2; 596904 2; 597871 2; 598965 2; 600060 2; 601156 2; 602253 2; 603351 2; 604450 2; 605550 2; 606651 2; 607753 2; 608685 2; 608856 2; 609960 2; 611065 2; 612171 2; 613278 2; 614386 2; 615495 2; 616605 2; 617716 2; 618828 2; 619941 2; 620620 2; 621055 2; 622170 2; 623286 2; 624403 2; 625521 2; 626640 2; 627760 2; 628881 2; 630003 2; 631126 2; 632250 2; 632710 2; 633375 2; 634501 2; 635376 2; 635628 2; 636756 2; 637885 2; 639015 2; 640146 2; 641278 2; 642411 2; 643545 2; 644680 2; 644956 2; 645816 2; 646646 2; 646953 2; 648091 2; 649230 2; 650370 2; 651511 2; 652653 2; 653796 2; 654940 2; 656085 2; 657231 2; 657359 2; 657800 2; 658008 2; 658378 2; 659526 2; 660675 2; 661825 2; 662976 2; 664128 2; 665281 2; 666435 2; 667590 2; 668746 2; 669903 2; 669920 2; 671061 2; 672220 2; 673380 2; 674541 2; 675703 2; 676866 2; 677040 2; 678030 2; 679195 2; 680361 2; 681528 2; 682640 2; 682696 2; 683865 2; 685035 2; 686206 2; 687378 2; 688551 2; 689725 2; 690900 2; 692076 2; 693253 2; 694431 2; 695520 2; 695610 2; 696790 2; 697971 2; 699153 2; 700336 2; 701520
2; 702705 2; 703891 2; 705078 2; 705432 1; 706266 2; 707455 2; 708561 2; 708645 2; 709836 2; 711028 2; 712221 2; 713415 2; 714610 2; 715806 2; 717003 2; 718201 2; 719400 2; 720600 2; 720720 2; 721764 2; 721801 2; 723003 2; 724206 2; 725410 2; 726615 2; 727821 2; 729028 2; 730236 2; 731445 2; 732655 2; 733866 2; 735078 2; 735130 2; 735471 2; 736281 2; 736291 2; 737505 2; 738720 2; 739936 2; 741153 2; 742371 2; 743590 2; 744810 2; 746031 2; 747253 2; 748476 2; 748660 2; 749398 2; 749700 2; 750925 2; 752151 2;
753378 2; 754606 2; 755835 2; 757065 2; 758296 2; 759528 2; 760761 2; 761995 2; 762355 2; 763230 2; 764466 2; 765703 2; 766480 2; 766941 2; 768180 2; 769420 2; 770661 2; 771903 2; 773146 2; 774390 2; 775635 2; 776216 2; 776881 2; 778128 2; 779376 2; 780625 2; 781875 2; 783126 2; 784378 2; 785631 2; 786885 2; 788140 2; 789396 2; 790244 2; 790653 2; 791911 2; 793170 2; 794430 2; 795691 2; 796953 2; 798216 2; 799480 2; 800745 2; 802011 2; 803278 2; 804440 2; 804546 2; 805815 2; 807085 2; 808356 2; 809628 2; 810901 2; 812175 2; 813450 2; 814385 2; 814726 2; 816003 2; 817190 2; 817281 2; 818560 2; 818805 2; 819840 2; 821121 2; 822403 2; 823686 2; 824970 2; 826255 2; 827541 2; 828828 2; 830116 2; 831405 2; 832695 2; 833340 2; 833986 2; 835278 2; 836571 2; 837865 2; 839160 2; 840456 2; 841753 2; 843051 2; 844350 2; 845650 2; 846951 2; 848046 2; 848253 2; 849556 2; 850668 2; 850860 2; 852165 2; 853471 2; 854778 2; 856086 2; 857395 2; 858705 2; 860016 2; 861328 2; 862641 2; 862924 2; 863955 2; 864501 2; 865270 2; 866586 2; 867903 2; 869221 2; 870540 2; 871860 2; 873181 2; 874503 2; 875826 2; 877150 2; 877975 2; 878475 2; 879801 2; 881128 2; 882456 2; 883785 2; 885115 2; 886446 2; 887778
2; 888030 2; 889111 2; 890445 2; 891780 2; 893116 2; 893200 2; 894453 2; 895791 2; 897130 2; 898470 2; 899811 2; 901153 2; 902496 2; 903840 2; 905185 2; 906192 2; 906531 2; 907878 2; 908600 2; 909226 2; 910575 2; 911925 2; 913276 2; 914628 2; 915981 2; 916895 2; 917335 2; 918690 2; 920046 2; 921403 2; 922761 2; 924120 2; 924176 2; 925480 2; 926841 2; 928203 2; 929566 2; 930930 2; 932295 2; 933661 2; 935028 2; 936396 2; 937765 2; 939135 2; 939929 2; 940506 2; 941878 2; 943251 2; 944625 2; 946000 2; 947376 2;
948753 2; 950131 2; 951510 2; 952890 2; 954271 2; 955653 2; 955860 2; 957036 2; 958420 2; 959805 2; 961191 2; 962578 2; 962598 2; 963966 2; 965355 2; 966745 2; 968136 2; 969528 2; 970921 2; 971635 2; 971970 2; 972315 2; 973710 2; 975106 2; 976503 2; 977901 2; 979300 2; 980700 2; 982101 2; 983503 2; 984906 2; 986310 2; 987715 2; 988260 2; 989121 2; 990528 2; 991936 2; 993345 2; 994755 2; 996166 2; 997578 2; 998991 2; 1000405 2; 1001820 2; 1003236 2; 1004653 2; 1004731 2; 1006071 2; 1007490 2; 1008910 2; 1010331 2; 1011753 2; 1013176 2; 1014600 2; 1016025 2; 1017451 2; 1018878 2; 1020306 2; 1021384 2; 1021735 2; 1023165 2; 1024596 2; 1026028 2; 1027461 2; 1028790 2; 1028895 2;
1030330 2; 1031766 2; 1033203 2; 1034641 2; 1036080 2; 1037520 2; 1038220 2; 1038961 2; 1040403 2; 1041846 2; 1043290 2; 1044735 2; 1046181 2; 1047628 2; 1049076 2; 1050525 2; 1051975 2; 1053426 2; 1054878 2; 1055240 2; 1056331 2; 1057785 2; 1059240 2; 1060696 2; 1062153 2; 1063611 2; 1065070 2; 1066530 2; 1067991 2; 1069453 2; 1070916 2; 1072380 2; 1072445 2; 1073845 2; 1075311 2; 1076778 2; 1078246 2; 1079715 2; 1081185 2; 1081575 2; 1082656 2; 1084128 2; 1085601 2; 1086008 2; 1087075 2; 1088430 2; 1088550 2; 1089836 2; 1090026 2; 1091503 2; 1092981 2; 1094460 2; 1095940 2; 1097421 2; 1098903 2; 1100386 2; 1101870 2; 1103355 2; 1104841 2; 1106328 2; 1107414 2; 1107568 2; 1107816 2; 1109305 2; 1110795 2; 1112286 2; 1113778 2; 1115271 2; 1116765 2; 1118260 2; 1119756 2; 1121253 2; 1122751 2; 1124250 2; 1125180 2; 1125750 2; 1127251 2; 1128753
2; 1130256 2; 1131760 2; 1133265 2; 1134771 2; 1136278 2; 1137786 2; 1139295 2; 1140805 2; 1142316 2; 1143135 2; 1143828 2; 1144066 2; 1145341 2; 1146855 2; 1148370 2; 1149886 2; 1150626 2; 1151403 2; 1152921 2; 1154440 2; 1155960 2; 1157481 2; 1159003 2; 1160526 2; 1161280 2; 1162050 2; 1163575 2; 1165101 2; 1166628 2; 1168156 2; 1169685 2; 1171215 2; 1172746 2; 1174278 2; 1175811 2; 1177345 2; 1178880 2; 1179616 2; 1180416 2; 1181953 2; 1183491 2; 1184040 2; 1185030 2; 1186570 2; 1188111 2; 1189653 2; 1191196 2; 1192740 2; 1194285 2; 1195831 2; 1197378 2; 1198144 2; 1198926 2; 1200475 2; 1202025 2; 1203576 2; 1205128 2; 1206681 2; 1208235 2; 1209790 2; 1211346 2; 1212903 2; 1214461 2; 1215450 2; 1216020 2; 1216865 2; 1217580 2; 1219141 2; 1220703 2; 1221759 2; 1222266 2; 1223830 2; 1225395 2; 1226961 2; 1228528 2; 1230096 2; 1231665 2; 1233235 2; 1234806 2; 1235780 2; 1236378 2; 1237951 2; 1239525 2; 1241100 2; 1242676 2; 1244253 2; 1245831 2; 1247410 2; 1248990 2; 1250571 2; 1252153 2; 1253736 2; 1254890 2;
1255320 2; 1256905 2; 1258491 2; 1260078 2; 1261666 2; 1263255 2; 1264845 2; 1266436 2; 1268028 2; 1269621 2; 1271215 2; 1272810 2; 1274196 2; 1274406 2; 1276003 2; 1277601 2; 1279200 2; 1280800 2; 1282401 2; 1282975 2; 1284003 2; 1285606 2; 1287210 2; 1288815 2; 1290421 2; 1292028 2; 1293636 2; 1293699 2; 1295245 2; 1296855 2; 1298466 2; 1300078 2; 1301691 2; 1303305 2; 1304920 2; 1306536 2; 1307504 2; 1308153 2; 1309771 2; 1311390 2; 1313010 2; 1313400 2; 1314631 2; 1316253 2; 1317876 2; 1319500 2; 1321125 2; 1322751 2; 1324378 2; 1326006 2; 1327635 2; 1329265 2; 1330896 2; 1332528 2; 1333300 2; 1334161 2; 1335795 2; 1337430 2; 1339066 2; 1340703 2; 1342341 2; 1343980 2; 1344904 2; 1345620 2; 1347261 2; 1348903 2; 1350546 2; 1352078 2; 1352190 2; 1353275 2; 1353400 2; 1353835 2; 1355481 2; 1357128 2; 1358776 2; 1360425 2; 1362075 2; 1363726
2; 1365378 2; 1367031 2; 1368685 2; 1370340 2; 1370754 2; 1371996 2; 1373653 2; 1373701 2; 1375311 2; 1376970 2; 1378630 2; 1380291 2; 1381953 2; 1383616 2; 1385280 2; 1386945 2; 1388611 2; 1390278 2; 1391946 2; 1393615 2; 1394204 2; 1395285 2; 1396956 2; 1398628 2; 1400301 2; 1401975 2; 1403650 2; 1405326 2; 1407003 2; 1408681 2; 1410360 2; 1412040 2; 1413721 2; 1414910 2; 1415403 2; 1417086 2; 1418770 2; 1420455 2; 1422141 2; 1423828 2; 1425516 2; 1426425 2; 1427205 2; 1428895 2; 1430586 2; 1432278 2; 1433971 2; 1435665 2; 1435820 2; 1437360 2; 1439056 2; 1440753 2; 1442451 2; 1444150 2; 1445850 2; 1447551 2; 1449253 2; 1450956 2; 1452660 2; 1454365 2; 1456071 2; 1456935 2; 1457778 2; 1459486 2; 1461195 2; 1462905 2; 1464616 2; 1466328 2; 1468041 2; 1469755 2; 1471470 2; 1473186 2; 1474903 2; 1476621 2; 1478256 2; 1478340 2; 1480060 2; 1481781 2; 1483503 2; 1485226 2; 1486950 2; 1488675 2; 1490401 2; 1492128 2; 1493856 2; 1495585 2; 1497315 2; 1499046 2; 1499784 2; 1500778 2; 1502501 2; 1502511 2; 1504245 2;
1505980 2; 1507716 2; 1509453 2; 1511191 2; 1512930 2; 1514670 2; 1516411 2; 1518153 2; 1519896 2; 1521520 2; 1521640 2; 1523385 2; 1525131 2; 1526878 2; 1528626 2; 1530375 2; 1532125 2; 1533876 2; 1533939 2; 1535628 2; 1537381 2; 1539135 2; 1540890 2; 1542646 2; 1543465 2; 1544403 2; 1546161 2; 1547920 2; 1549680 2; 1551441 2; 1553203 2; 1554966 2; 1556730 2; 1558495 2; 1560261 2; 1560780 2; 1562028 2; 1562275 2; 1563796 2; 1565565 2; 1565620 2; 1567335 2; 1569106 2; 1570878 2; 1572651 2; 1574425 2; 1576200 2; 1577976 2; 1579753 2; 1581531 2; 1581580 2; 1583310 2; 1585090 2; 1586871 2; 1587986 2; 1588653 2; 1590436 2; 1592220 2; 1594005 2; 1595791 2; 1597578 2; 1599366 2; 1601155 2; 1602945 2; 1604736 2; 1606528 2; 1608321 2; 1610115 2; 1610564 2; 1611910 2; 1613706 2; 1615503 2; 1617301 2; 1619100 2; 1620900 2; 1622701 2; 1623160 2; 1624503
2; 1626306 2; 1628110 2; 1629915 2; 1631721 2; 1633355 2; 1633528 2; 1635336 2; 1637145 2; 1638955 2; 1640766 2; 1642578 2; 1644391 2; 1646205 2; 1648020 2; 1649836 2; 1651653 2; 1653471 2; 1655290 2; 1656360 2; 1657110 2; 1658931 2; 1660753 2; 1662576 2; 1663740 2; 1664400 2; 1666225 2; 1668051 2; 1669878 2; 1671706 2; 1673535 2; 1675365 2; 1677196 2; 1679028 2; 1679580 2; 1680861 2; 1682695 2; 1684530 2; 1686366 2; 1688203 2; 1690041 2; 1691880 2; 1693720 2; 1695561 2; 1697403 2; 1699246 2; 1701090 2; 1702935 2; 1703016 2; 1704781 2; 1706628 2; 1708476 2; 1710325 2; 1712175 2; 1712304 2; 1714026 2; 1715878 2; 1717731 2; 1719585 2; 1721440 2; 1723296 2; 1725153 2; 1726669 2; 1727011 2; 1728870 2; 1730730 2; 1732591 2; 1734453 2; 1736316 2; 1738180 2; 1740045 2; 1741911 2; 1743778 2; 1745646 2; 1747515 2; 1749060 2; 1749385 2; 1750540 2; 1751256 2; 1753128 2; 1755001 2; 1756875 2; 1758750 2; 1760626 2; 1762503 2; 1764381 2; 1766260 2; 1768140 2; 1770021 2; 1771903 2; 1773786 2; 1774630 2; 1775670 2; 1777555 2;
1779441 2; 1781328 2; 1783216 2; 1785105 2; 1786995 2; 1788886 2; 1790778 2; 1792671 2; 1794565 2; 1796460 2; 1798356 2; 1798940 2; 1800253 2; 1802151 2; 1804050 2; 1805950 2; 1807851 2; 1809753 2; 1811656 2; 1813560 2; 1815465 2; 1817371 2; 1819278 2; 1821186 2; 1823095 2; 1823471 2; 1825005 2; 1826916 2; 1828828 2; 1830741 2; 1832655 2; 1834570 2; 1836486 2; 1837620 2; 1838403 2; 1840321 2; 1842240 2; 1844160 2; 1846081 2; 1848003 2; 1848224 2; 1849926 2; 1851850 2; 1853775 2; 1855701 2; 1857628 2; 1859556 2; 1861485 2; 1863415 2; 1865346 2; 1867278 2; 1869211 2; 1871145 2; 1873080 2; 1873200 2; 1875016 2; 1876953 2; 1878891 2; 1880830 2; 1882770 2; 1884711 2; 1886653 2; 1888596 2; 1890540 2; 1892485 2; 1894431 2; 1896378 2; 1898326 2; 1898400 2; 1900275 2; 1902225 2; 1904176 2; 1906128 2; 1906884 2; 1908081 2; 1910035 2; 1911990 2; 1913946
2; 1915903 2; 1917861 2; 1919820 2; 1921780 2; 1923741 2; 1923825 2; 1925703 2; 1927666 2; 1929501 2; 1929630 2; 1931595 2; 1933561 2; 1935528 2; 1937496 2; 1939465 2; 1941435 2; 1943406 2; 1945378 2; 1947351 2; 1947792 2; 1949325 2; 1949476 2; 1951300 2; 1953276 2; 1955253 2; 1957231 2; 1959210 2; 1961190 2; 1961256 2; 1963171 2; 1965153 2; 1967136 2; 1969120 2; 1971105 2; 1973091 2; 1975078 2; 1975354 2; 1977066 2; 1979055 2; 1981045 2; 1983036 2; 1985028 2; 1987021 2; 1989015 2; 1991010 2; 1993006 2; 1995003 2; 1997001 2; 1999000 2; 2001000 2; 2001460 2; 2003001 2; 2005003 2; 2007006 2; 2009010 2; 2011015 2; 2013021 2; 2015028 2; 2017036 2; 2019045 2; 2021055 2; 2023066 2; 2024785 2; 2025078 2; 2027091 2; 2027795 2; 2029105 2; 2031120 2; 2033136 2; 2035153 2; 2035800 2; 2037171 2; 2039190 2; 2041210 2; 2042975 2; 2043231 2; 2045253 2; 2047276 2; 2049300 2; 2051325 2; 2053351 2; 2054360 2; 2055378 2; 2057406 2; 2059435 2; 2061465 2; 2063496 2; 2065528 2; 2067561 2; 2069595 2; 2071630 2; 2073666 2; 2075703 2;
2077741 2; 2079780 2; 2081156 2; 2081820 2; 2083861 2; 2085903 2; 2087946 2; 2089990 2; 2092035 2; 2094081 2; 2096128 2; 2098176 2; 2100225 2; 2102275 2; 2104326 2; 2106378 2; 2108184 2; 2108431 2; 2110485 2; 2112540 2; 2114596 2; 2116653 2; 2118711 2; 2118760 2; 2120770 2; 2122830 2; 2123555 2; 2124891 2; 2126953 2; 2129016 2; 2131080 2; 2133145 2; 2135211 2; 2135445 2; 2137278 2; 2139346 2; 2141415 2; 2143485 2; 2145556 2; 2147628 2; 2149701 2; 2151775 2; 2153850 2; 2155926 2; 2158003 2; 2160081 2; 2162160 2; 2162940 2; 2164240 2; 2166321 2; 2168403 2; 2170486 2; 2172570 2; 2174655 2; 2176741 2; 2178828 2; 2180916 2; 2183005 2; 2185095 2; 2187186 2; 2189278 2; 2190670 2; 2191371 2; 2193465 2; 2195560 2; 2197656 2; 2199753 2; 2201851 2; 2203950 2; 2206050 2; 2208151 2; 2210253 2; 2212356 2; 2214460 2; 2216565 2; 2218636 2; 2218671 2; 2220075
2; 2220778 2; 2222886 2; 2224995 2; 2225895 2; 2227105 2; 2229216 2; 2231328 2; 2233441 2; 2235555 2; 2237670 2; 2239786 2; 2241903 2; 2244021 2; 2246140 2; 2246839 2; 2248260 2; 2250381 2; 2252503 2; 2254626 2; 2256750 2; 2258875 2; 2261001 2; 2263128 2; 2265256 2; 2267385 2; 2269515 2; 2271646 2; 2273778 2; 2275280 2; 2275911 2; 2278045 2; 2280180 2; 2282316 2; 2284453 2; 2286591 2; 2288730 2; 2290870 2; 2293011 2; 2295153 2; 2297296 2; 2299440 2; 2301585 2; 2303731 2; 2303960 2; 2305878 2; 2308026 2; 2310175 2; 2312325 2; 2314476 2; 2316628 2; 2318781 2; 2320935 2; 2323090 2; 2324784 2; 2325246 2; 2327403 2; 2329561 2; 2331720 2; 2331890 2; 2332880 2; 2333880 2; 2336041 2; 2338203 2; 2340366 2; 2342530 2; 2344695 2; 2346861 2; 2349028 2; 2349060 2; 2351196 2; 2353365 2; 2355535 2; 2357706 2; 2359878 2; 2362041 2; 2362051 2; 2364225 2; 2366400 2; 2368576 2; 2370753 2; 2372931 2; 2375110 2; 2377290 2; 2379471 2; 2381653 2; 2383836 2; 2386020 2; 2388205 2; 2390391 2; 2391444 2; 2392578 2; 2394766 2; 2396955 2;
2399145 2; 2401336 2; 2403528 2; 2405721 2; 2407915 2; 2410110 2; 2412306 2; 2414503 2; 2416701 2; 2418900 2; 2421090 2; 2421100 2; 2423301 2; 2425503 2; 2427706 2; 2429910 2; 2432115 2; 2434321 2; 2436528 2; 2438736 2; 2440945 2; 2441626 2; 2443155 2; 2445366 2; 2447578 2; 2449791 2; 2450980 2; 2452005 2; 2454220 2; 2456436 2; 2458653 2; 2460871 2; 2463090 2; 2465310 2; 2467531 2; 2469753 2; 2471976 2; 2474200 2; 2476425 2; 2478651 2; 2480878 2; 2481115 2; 2483106 2; 2485335 2; 2487565 2; 2489796 2; 2492028 2; 2494261 2; 2496144 2; 2496495 2; 2498730 2; 2500966 2; 2503203 2; 2505441 2; 2507680 2; 2509920 2; 2511496 2; 2512161 2; 2514403 2; 2516646 2; 2518890 2; 2521135 2; 2523381 2; 2525628 2; 2527876 2; 2530125 2; 2532375 2; 2534626 2; 2536878 2; 2539131 2; 2541385 2; 2542124 2; 2543640 2; 2545896 2; 2548153 2; 2550411 2; 2552670 2; 2554930
2; 2555190 2; 2557191 2; 2559453 2; 2561716 2; 2563980 2; 2566245 2; 2568511 2; 2570778 2; 2573000 2; 2573046 2; 2575315 2; 2577585 2; 2579856 2; 2582128 2; 2584401 2; 2586675 2; 2588950 2; 2591226 2; 2593503 2; 2595781 2; 2598060 2; 2598960 2; 2600340 2; 2602621 2; 2604125 2; 2604903 2; 2607186 2; 2609470 2; 2611755 2; 2614041 2; 2616328 2; 2618616 2; 2620905 2; 2623195 2; 2625486 2; 2627778 2; 2629575 2; 2630071 2; 2632365 2; 2634660 2; 2635500 2; 2636956 2; 2639253 2; 2641551 2; 2643850 2; 2646150 2; 2648451 2; 2650753 2; 2653056 2; 2655360 2; 2657665 2; 2659971 2; 2662278 2; 2664586 2; 2666895 2; 2667126 2; 2669205 2; 2671516 2; 2672670 2; 2673828 2; 2676141 2; 2678455 2; 2680770 2; 2683086 2; 2685403 2; 2687721 2; 2690040 2; 2692360 2; 2694681 2; 2697003 2; 2699004 2; 2699326 2; 2701650 2; 2703975 2; 2704156 1; 2706301 2; 2708628 2; 2710956 2; 2713285 2; 2715615 2; 2717946 2; 2720278 2; 2722611 2; 2724945 2; 2727280 2; 2729616 2; 2731135 2; 2731953 2; 2734291 2; 2736630 2; 2738970 2; 2741311 2; 2743653 2;
2745996 2; 2748340 2; 2750685 2; 2753031 2; 2755378 2; 2757726 2; 2760075 2; 2760681 2; 2762425 2; 2763520 2; 2764776 2; 2767128 2; 2769481 2; 2771835 2; 2774190 2; 2776546 2; 2778903 2; 2781261 2; 2783620 2; 2785980 2; 2788341 2; 2790703 2; 2793066 2; 2794155 2; 2795430 2; 2796160 2; 2797795 2; 2800161 2; 2802528 2; 2804896 2; 2807265 2; 2809635 2; 2812006 2; 2814378 2; 2816751 2; 2819125 2; 2821500 2; 2823876 2; 2826253 2; 2828631 2; 2829056 2; 2831010 2; 2833390 2; 2835771 2; 2838153 2; 2840536 2; 2842920 2; 2845305 2; 2847691 2; 2850078 2; 2852466 2; 2854855 2; 2857245 2; 2859636 2; 2862028 2; 2862209 2; 2864421 2; 2866815 2; 2869210 2; 2869685 2; 2871606 2; 2874003 2; 2876401 2; 2878800 2; 2881200 2; 2883601 2; 2886003 2; 2888406 2; 2890810 2; 2893215 2; 2895620 2; 2895621 2; 2898028 2; 2900436 2; 2902845 2; 2905255 2; 2907666 2; 2910078
2; 2912491 2; 2914905 2; 2917320 2; 2919735 2; 2919736 2; 2922153 2; 2924571 2; 2926990 2; 2929290 2; 2929410 2; 2931831 2; 2934253 2; 2936676 2; 2939100 2; 2941525 2; 2943951 2; 2946378 2; 2948806 2; 2951235 2; 2953665 2; 2956096 2; 2958528 2; 2960961 2; 2963220 2; 2963395 2; 2965830 2; 2968266 2; 2970703 2; 2973141 2; 2975580 2; 2978020 2; 2980461 2; 2982903 2; 2985346 2; 2987790 2; 2990235 2; 2992681 2; 2995128 2; 2997411 2; 2997576 2; 3000025 2; 3002475 2; 3004926 2; 3007378 2; 3009831 2; 3012285 2; 3014740 2; 3017196 2; 3019653 2; 3022111 2; 3024570 2; 3027030 2; 3029491 2; 3031864 2; 3031953 2; 3034416 2; 3036880 2; 3039345 2; 3041811 2; 3044278 2; 3046746 2; 3049215 2; 3049501 2; 3051685 2; 3054156 2; 3056628 2; 3059101 2; 3061575 2; 3064050 2; 3066526 2; 3066580 2; 3069003 2; 3071481 2; 3073960 2; 3076440 2; 3078921 2; 3081403 2; 3083886 2; 3086370 2; 3088855 2; 3091341 2; 3093828 2; 3096316 2; 3098805 2; 3101295 2; 3101560 2; 3103786 2; 3106278 2; 3108105 2; 3108771 2; 3111265 2; 3113760 2; 3116256 2;
3118753 2; 3121251 2; 3123750 2; 3124550 2; 3126250 2; 3128751 2; 3131253 2; 3133756 2; 3136260 2; 3136805 2; 3138765 2; 3141271 2; 3143778 2; 3146286 2; 3148795 2; 3151305 2; 3153816 2; 3156328 2; 3158841 2; 3161355 2; 3162510 2; 3163870 2; 3166386 2; 3168903 2; 3171421 2; 3172316 2; 3173940 2; 3176460 2; 3178981 2; 3181503 2; 3183545 2; 3184026 2; 3186550 2; 3189075 2; 3191601 2; 3194128 2; 3196656 2; 3199185 2; 3201715 2; 3204246 2; 3206778 2; 3208094 2; 3209311 2; 3211845 2; 3214380 2; 3216916 2; 3219453 2; 3221991 2; 3224530 2; 3227070 2; 3229611 2; 3232153 2; 3234696 2; 3237240 2; 3239785 2; 3242331 2; 3244140 2; 3244878 2; 3247426 2; 3249975 2; 3252525 2; 3255076 2; 3257628 2; 3260181 2; 3262623 2; 3262735 2; 3265290 2; 3267846 2; 3268760 2; 3270403 2; 3272961 2; 3275520 2; 3278080 2; 3280455 2; 3280641 2; 3283203 2; 3285766 2; 3288330
2; 3290895 2; 3293461 2; 3296028 2; 3298596 2; 3301165 2; 3303735 2; 3306306 2; 3308878 2; 3311451 2; 3314025 2; 3316600 2; 3317040 2; 3319176 2; 3321753 2; 3321960 2; 3324331 2; 3326910 2; 3329490 2; 3332071 2; 3334653 2; 3337236 2; 3339820 2; 3342405 2; 3344991 2; 3347578 2; 3350166 2; 3352755 2; 3353896 2; 3355345 2; 3357936 2; 3360528 2; 3363121 2; 3365715 2; 3365856 2; 3368310 2; 3370906 2; 3373503 2; 3376101 2; 3378700 2; 3381300 2; 3383901 2; 3386503 2; 3389106 2; 3391024 2; 3391710 2; 3394315 2; 3396921 2; 3399528 2; 3402136 2; 3404745 2; 3407355 2; 3409966 2; 3412578 2; 3415191 2; 3417805 2; 3420420 2; 3423036 2; 3425653 2; 3428271 2; 3428425 2; 3430890 2; 3433510 2; 3436131 2; 3438753 2; 3441376 2; 3444000 2; 3446625 2; 3449251 2; 3451878 2; 3454506 2; 3457135 2; 3459765 2; 3462396 2; 3464840 2; 3465028 2; 3466100 2; 3467661 2; 3470295 2; 3472930 2; 3475566 2; 3478203 2; 3478761 2; 3480841 2; 3483480 2; 3486120 2; 3488761 2; 3491403 2; 3494046 2; 3496690 2; 3499335 2; 3501981 2; 3504050 2; 3504628 2;
3507276 2; 3509925 2; 3512575 2; 3515226 2; 3517878 2; 3520531 2; 3523185 2; 3525840 2; 3528496 2; 3531153 2; 3533811 2; 3536470 2; 3539130 2; 3541791 2; 3542276 2; 3544453 2; 3547116 2; 3549780 2; 3552445 2; 3555111 2; 3557778 2; 3560446 2; 3563115 2; 3565785 2; 3568456 2; 3571128 2; 3573801 2; 3576475 2; 3579150 2; 3580779 2; 3581826 2; 3584503 2; 3587181 2; 3589860 2; 3592540 2; 3595221 2; 3597903 2; 3600586 2; 3603270 2; 3605955 2; 3608641 2; 3611328 2; 3612280 2; 3614016 2; 3616705 2; 3619395 2; 3619560 2; 3622086 2; 3624778 2; 3627471 2; 3630165 2; 3632860 2; 3635556 2; 3638253 2; 3640951 2; 3643650 2; 3646350 2; 3649051 2; 3651753 2; 3654456 2; 3657160 2; 3658620 2; 3659865 2; 3662571 2; 3665278 2; 3667986 2; 3670695 2; 3673405 2; 3676116 2; 3678828 2; 3681541 2; 3684255 2; 3686970 2; 3689686 2; 3692403 2; 3695121 2; 3697840 2; 3697960
2; 3700560 2; 3703281 2; 3706003 2; 3708726 2; 3711450 2; 3714175 2; 3716901 2; 3719628 2; 3722356 2; 3725085 2; 3727815 2; 3730546 2; 3733278 2; 3736011 2; 3737581 2; 3738745 2; 3741480 2; 3744216 2; 3746953 2; 3749691 2; 3752430 2; 3755170 2; 3757911 2; 3760653 2; 3763396 2; 3764376 2; 3766140 2; 3768885 2; 3771631 2; 3774378 2; 3777126 2; 3777484 2; 3779875 2; 3782625 2; 3785376 2; 3788128 2; 3790881 2; 3793635 2; 3796390 2; 3799146 2; 3801903 2; 3804661 2; 3807420 2; 3810180 2; 3812941 2; 3815703 2; 3817670 2; 3818466 2; 3819816 2; 3821230 2; 3823995 2; 3826761 2; 3829528 2; 3832296 2; 3835065 2; 3837835 2; 3838380 2; 3840606 2; 3843378 2; 3846151 2; 3848925 2; 3851700 2; 3854476 2; 3857253 2; 3858140 2; 3860031 2; 3862810 2; 3865590 2; 3868371 2; 3871153 2; 3873936 2; 3876720 2; 3879505 2; 3882291 2; 3885078 2; 3887866 2; 3890655 2; 3893445 2; 3896236 2; 3898895 2; 3899028 2; 3901821 2; 3904615 2; 3907410 2; 3910206 2; 3913003 2; 3915801 2; 3918600 2; 3921225 2; 3921400 2; 3924201 2; 3927003 2; 3929806 2;
3932610 2; 3935415 2; 3938221 2; 3939936 2; 3941028 2; 3943836 2; 3946645 2; 3949455 2; 3952266 2; 3955078 2; 3957891 2; 3960705 2; 3963520 2; 3966336 2; 3969153 2; 3971971 2; 3974790 2; 3977610 2; 3980431 2; 3981264 2; 3983253 2; 3986076 2; 3988900 2; 3991725 2; 3994551 2; 3997378 2; 4000206 2; 4003035 2; 4005865 2; 4008696 2; 4011528 2; 4014361 2; 4017195 2; 4020030 2; 4022866 2; 4022880 2; 4025703 2; 4028541 2; 4031380 2; 4034220 2; 4037061 2; 4039903 2; 4042746 2; 4045590 2; 4048435 2; 4051281 2; 4054128 2; 4056976 2; 4059825 2; 4062675 2; 4064785 2; 4065526 2; 4068378 2; 4071231 2; 4074085 2; 4076940 2; 4079796 2; 4082653 2; 4082925 2; 4085511 2; 4088370 2; 4091230 2; 4094091 2; 4096953 2; 4099816 2; 4102680 2; 4105545 2; 4106980 2; 4108411 2; 4111278 2; 4114146 2; 4117015 2; 4119885 2; 4122756 2; 4125628 2; 4128501 2; 4131375 2; 4134250
2; 4137126 2; 4140003 2; 4142881 2; 4145760 2; 4148640 2; 4149466 2; 4151521 2; 4154403 2; 4157286 2; 4160170 2; 4163055 2; 4165941 2; 4168828 2; 4171716 2; 4174605 2; 4177495 2; 4180386 2; 4183278 2; 4186171 2; 4187106 2; 4189065 2; 4191960 2; 4192244 2; 4194856 2; 4197753 2; 4200651 2; 4203550 2; 4206450 2; 4209351 2; 4212253 2; 4215156 2; 4218060 2; 4220965 2; 4223871 2; 4226778 2; 4229686 2; 4232595 2; 4235315 2; 4235505 2; 4238416 2; 4241328 2; 4244241 2; 4247155 2; 4249575 2; 4250070 2; 4252986 2; 4255903 2; 4258821 2; 4261740 2; 4264660 2; 4267581 2; 4270503 2; 4272048 2; 4273426 2; 4276350 2; 4278680 2; 4279275 2; 4282201 2; 4285128 2; 4288056 2; 4290985 2; 4292145 2; 4293915 2; 4296846 2; 4299778 2; 4302711 2; 4305645 2; 4308580 2; 4311516 2; 4314453 2; 4317391 2; 4320330 2; 4322340 2; 4323270 2; 4326211 2; 4329153 2; 4332096 2; 4335040 2; 4337985 2; 4340931 2; 4343878 2; 4346826 2; 4349775 2; 4352725 2; 4355676 2; 4358628 2; 4361581 2; 4364535 2; 4366296 2; 4367490 2; 4370446 2; 4373403 2; 4376361 2;
4379320 2; 4382280 2; 4385241 2; 4388203 2; 4391166 2; 4394130 2; 4397095 2; 4400061 2; 4403028 2; 4405996 2; 4408965 2; 4410549 2; 4411935 2; 4414906 2; 4417878 2; 4420851 2; 4421275 2; 4423825 2; 4426800 2; 4429776 2; 4432753 2; 4435731 2; 4438710 2; 4441690 2; 4444671 2; 4447653 2; 4450636 2; 4453620 2; 4455100 2; 4456605 2; 4457400 2; 4459591 2; 4462578 2; 4465566 2; 4468555 2; 4471545 2; 4474536 2; 4477528 2; 4480521 2; 4483515 2; 4486510 2; 4489506 2; 4492503 2; 4495501 2; 4496388 2; 4498500 2; 4499950 2; 4501500 2; 4504501 2; 4507503 2; 4545100 2; 4582116 2; 4590551 2; 4598126 2; 4636304 2; 4682360 2; 4686825 2; 4728720 2; 4775385 2; 4780230 2; 4822356 2; 4869634 2; 4917220 2; 4965115 2; 4967690 2; 5006386 2; 5013320 2; 5061836 2; 5110664 2; 5159805 2; 5160610 2; 5200300 2; 5209260 2; 5245786 2; 5259030 2; 5309116 2; 5311735 2; 5359095
2; 5359519 2; 5379616 2; 5410240 2; 5461280 2; 5461512 2; 5512640 2; 5563251 2; 5564321 2; 5616324 2; 5668650 2; 5721300 2; 5773185 2; 5774275 2; 5827576 2; 5852925 2; 5881204 2; 5935160 2; 5949147 2; 5989005 2; 5989445 2; 6044060 2; 6096454 2; 6099006 2; 6154284 2; 6209895 2; 6210820 2; 6265840 2; 6322120 2; 6378736 2; 6435689 2; 6438740 2; 6471002 2; 6492980 2; 6550610 2; 6608580 2; 6666891 2; 6672876 2; 6724520 2; 6725544 2; 6784540 2; 6843880 2; 6903565 2; 6906900 2; 6913340 2; 6963596 2; 7023974 2; 7028847 2; 7059052 2; 7084700 2; 7145775 2; 7160245 2; 7207200 2; 7268976 2; 7331104 2; 7393585 2; 7413705 2; 7456420 2; 7519610 2; 7583156 2; 7624512 2; 7647059 2; 7673835 2; 7711320 2; 7726160 2; 7775940 2; 7840920 2; 7888725 2; 7906261 2; 7940751 2; 7971964 2; 8038030 2; 8104460 2; 8145060 2; 8171255 2; 8214570 2; 8238416 2; 8259888 2; 8305944 2; 8347680 2; 8373840 2; 8436285 2; 8442105 2; 8495410 2; 8510740 2; 8579746 2; 8649124 2; 8718875 2; 8783390 2; 8789000 2; 8859500 2; 8930376 2; 8936928 2; 9001629 2;
9073260 2; 9078630 2; 9145270 2; 9217660 2; 9290431 2; 9363584 2; 9366819 2; 9381251 2; 9437120 2; 9511040 2; 9585345 2; 9657648 2; 9657700 2; 9660036 2; 9691375 2; 9735114 2; 9810580 2; 9886435 2; 9962680 2; 10009125 2; 10015005 2; 10039316 2; 10116344 2; 10193765 2; 10271580 2; 10295472 2; 10334625 2; 10349790 2; 10400600 1; 10424128 2; 10428396 2; 10507399 2; 10518300 2; 10586800 2; 10666600 2; 10668000 2; 10737573 2; 10746800 2; 10827401 2; 10908404 2; 10989810 2; 11009376 2; 11071620 2; 11153835 2; 11236456 2; 11238513 2; 11319484 2; 11358880 2; 11402920 2; 11486765 2; 11571020 2; 11655686 2; 11716640 2; 11740764 2; 11826255 2; 11912160 2; 11998480 2; 12082785 2; 12085216 2; 12103014 2; 12172369 2; 12259940 2; 12271512 2; 12347930 2; 12436340 2; 12457445 2; 12525171 2; 12614424 2; 12620256 2; 12704100 2; 12794200 2; 12840751 2; 12884725 2; 12975676 2; 13019909 2; 13037895 2; 13067054 2; 13123110 2; 13158860 2; 13232835 2; 13251095 2; 13343760 2; 13436856 2; 13530384 2; 13624345 2; 13633830 2; 13718740 2; 13813570 2; 13884156 2; 13908836 2; 13983816 2; 13991544 2; 14004539 2; 14043870 2; 14100680 2; 14197260 2; 14294280 2; 14307150 2; 14391741 2; 14463090 2; 14489644 2; 14587990 2; 14686780 2; 14786015 2; 14885696 2; 14891626 2; 14985824 2; 15020334 2; 15086400 2; 15187425 2; 15288900 2; 15329615 2; 15380937 2; 15390826 2; 15493204 2; 15596035 2; 15699320 2; 15777195 2; 15803060 2; 15890700 2; 15907256 2; 16011909 2; 16108764 2; 16117020 2; 16222590 2; 16234505 2; 16328620 2; 16435111 2; 16542064 2; 16649480 2; 16701685 2; 16757360 2; 16865705 2; 16974516 2; 17083794 2; 17178876 2; 17193540 2; 17259390 2; 17303755 2; 17383860 2; 17414440 2; 17525596 2; 17637224 2; 17666220 2; 17749325 2; 17861900 2; 17974950 2; 18009460 2; 18088476 2; 18156204 2; 18163860 2; 18202479 2; 18316960 2; 18431920 2; 18474840 2; 18547360 2; 18643560 2; 18663281 2; 18671940 2; 18779684 2; 18896570 2; 19013940 2; 19131795 2; 19190605 2; 19250136 2; 19368964 2; 19488280 2; 19608085 2; 19720001 2; 19728380 2; 19757815 2; 19849166 2; 19970444 2; 20030010 2; 20058300 2; 20092215 2; 20160075 2; 20214480 2; 20260275 2; 20337240 2; 20358520 2; 20460496 2; 20584249 2; 20708500 2; 20811575 2; 20833250 2; 20958500 2; 21084251 2; 21111090 2; 21210504 2; 21337260 2; 21374050 2; 21464520 2; 21474180 2; 21592285 2; 21720556 2; 21849334 2; 21947850 2; 21978620 2; 22108415 2; 22238720 2; 22369536 2; 22481940 2; 22500864 2; 22533126 2; 22537515 2; 22632705 2; 22765060 2; 22897930 2; 22957480 2; 23031316 2; 23130030 2; 23165219 2; 23299640 2; 23434580 2; 23535820 2; 23570040 2; 23706021 2; 23738715 2; 23842524 2; 23979550 2; 24040016 2; 24117100 2; 24255175 2; 24359335 2; 24393776 2; 24532904 2; 24672560 2; 24812745 2; 24953460 2; 24992045 2; 25094706 2; 25236484 2; 25378795 2; 25521640 2; 25621596 2; 25637001 2; 25665020 2; 25808936 2; 25827165 2; 25953389 2; 26098380 2; 26243910 2; 26294360 2; 26389980 2; 26536591 2; 26683744 2; 26831440 2; 26964280 2; 26978328 2; 26979680 2; 27128465 2; 27277796 2; 27285336 2; 27427674 2; 27578100 2; 27646920 2; 27729075 2; 27880600 2; 28032676 2; 28048800 2; 28185304 2; 28338485 2; 28342440 2; 28492220 2; 28646510 2; 28801356 2; 28956759 2; 28989675 2; 29034396 2; 29051001 2; 29112720 2; 29269240 2; 29426320 2; 29583961 2; 29742164 2; 29772765 2; 29900930 2; 30045015 2; 30060260 2; 30220155 2; 30260340 2; 30380616 2; 30421755 2; 30507895 2; 30541644 2; 30703240 2; 30865405 2; 30872016 2; 31028140 2; 31191446 2; 31256555 2; 31355324 2; 31519775 2; 31684800 2; 31850400 2; 32016576 2; 32018910 2; 32183329 2; 32224114 2; 32350660 2; 32468436 2; 32518570 2; 32687060 2; 32795126 2; 32801517 2; 32856131 2; 33025784 2; 33196020 2; 33366840 2; 33538245 2; 33585370 2; 33710236 2; 33882814 2; 34055980 2; 34229735 2; 34389810 2; 34404080 2; 34579016 2; 34597290 2; 34754544 2; 34826302 2; 34930665 2; 35107380 2; 35208615 2; 35284690 2; 35462596 2; 35641099 2; 35820200 2; 35999900 2; 36041955 2; 36180200 2; 36288252 2; 36361101 2; 36542604 2; 36724710 2; 36890001 2; 36907420 2; 36949857 2; 37090735 2; 37274656 2; 37442160 2; 37459184 2; 37644320 2; 37752925 2; 37830065 2; 38016420 2; 38203386 2; 38320568 2; 38390964 2; 38567100 2; 38579155 2; 38608020 2; 38630900 2; 38767960 2; 38957380 2; 39147416 2; 39175752 2; 39338069 2; 39524100 2; 39529340 2; 39721230 2; 39913740 2; 40106871 2; 40116600 1; 40300624 2; 40432700 2; 40475358 2; 40495000 2; 40690000 2; 40885625 2; 41081876 2; 41278754 2; 41356876 2; 41476260 2; 41507642 2; 41674395 2; 41873160 2; 42072556 2; 42272584 2; 42296805 2; 42473245 2; 42674540 2; 42876470 2; 43079036 2; 43252665 2; 43282239 2; 43486080 2; 43690560 2; 43895680 2; 43949268 2; 44101441 2; 44224635 2; 44307844 2; 44352165 2; 44514890 2; 44722580 2; 44930915 2; 45057474 2; 45139896 2; 45212895 2; 45349524 2; 45379620 2; 45559800 2; 45770725 2; 45982300 2; 46194526 2; 46217626 2; 46407404 2; 46504458 2; 46620935 2; 46835120 2; 47049960 2; 47239010 2; 47265456 2; 47481609 2; 47698420 2; 47915890 2; 48134020 2; 48277230 2; 48352811 2; 48572264 2; 48792380 2; 48903492 2; 49013160 2; 49177128 2; 49234605 2; 49332470 2; 49456716 2; 49679494 2; 49902940 2; 50063860 2; 50127055 2; 50351840 2; 50404915 2; 50577296 2; 50803424 2; 51030225 2; 51257700 2; 51485850 2; 51494751 2; 51714676 2; 51895935 2; 51944179 2; 51971283 2; 52174360 2; 52405220 2; 52451256 2; 52602165 2; 52636760 2; 52868981 2; 53101884 2; 53335470 2; 53524680 2; 53569740 2; 53727345 2; 53804695 2; 54040336 2; 54276664 2; 54513680 2; 54627300 2; 54751385 2; 54870480 2; 54891018 2; 54989780 2; 55228866 2; 55468644 2; 55525372 2; 55709115 2; 55950280 2; 56031760 2; 56192140 2; 56434696 2; 56677949 2; 56921900 2; 57166550 2; 57211376 2; 57411900 2; 57657951 2; 57904704 2; 57940519 2; 58152160 2; 58400320 2; 58409520 2; 58649185 2; 58898756 2; 59149034 2; 59400020 2; 59626385 2; 59651715 2; 59904120 2; 60157236 2; 60411064 2; 60665605 2; 60862165 2; 60920860 2; 61124064 2; 61176830 2; 61433516 2; 61474519 2; 61523748 2; 61690919 2; 61949040 2; 62117055 2; 62207880 2; 62467440 2; 62727721 2; 62891499 2; 62988724 2; 63250450 2; 63391251 2; 63512900 2; 63776075 2; 64039976 2; 64304604 2; 64446024 2; 64512240 2; 64569960 2; 64684950 2; 64836045 2; 65102860 2; 65370406 2; 65638684 2; 65907695 2; 65998350 2; 66177440 2; 66447920 2; 66719136 2; 66991089 2; 67263780 2; 67331650 2; 67537210 2; 67811380 2; 67863915 2; 67910864 2; 67945521 2; 68086291 2; 68361944 2; 68638340 2; 68685050 2; 68915480 2; 69193365 2; 69471996 2; 69751374 2; 70031500 2; 70058751 2; 70312375 2; 70594000 2; 70607460 2; 70876376 2; 71159504 2; 71443385 2; 71452955 2; 71523144 2; 71728020 2; 72013410 2; 72299556 2; 72586459 2; 72867865 2; 72874120 2; 73162540 2; 73451720 2; 73629072 2; 73741661 2; 74032364 2; 74303685 2; 74323830 2; 74616060 2; 74909055 2; 74974368 2; 75202816 2; 75287520 2; 75497344 2; 75760620 2; 75792640 2; 76088705 2; 76385540 2; 76683146 2; 76904685 2; 76981524 2; 77238876 2; 77280675 2; 77558760 2; 77580600 2; 77881300 2; 78182776 2; 78485029 2; 78738660 2; 78788060 2; 79091870 2; 79208745 2; 79396460 2; 79701831 2; 80007984 2; 80260180 2; 80314920 2; 80622640 2; 80931145 2; 81240436 2; 81550514 2; 81803645 2; 81861380 2; 82173035 2; 82485480 2; 82598880 2; 82798716 2; 83112744 2; 83291670 2; 83369265 2; 83427565 2; 83743180 2; 84059590 2; 84376796 2; 84672315 2; 84694799 2; 84957251 2; 85013600 2; 85333200 2; 85653600 2; 85900584 2; 85974801 2; 86296804 2; 86493225 2; 86567815 2; 86619610 2; 86943220 2; 87267635 2; 87541245 2; 87592856 2; 87918884 2; 88201170 2; 88245720 2; 88573365 2; 88901820 2; 89231086 2; 89561164 2; 89857530 2; 89892055 2; 90223760 2; 90556280 2; 90858768 2; 90889616 2; 91223769 2; 91537110 2; 91558740 2; 91894530 2; 91962520 2; 92231140 2; 92561040 2; 92568571 2; 92906824 2; 93240126 2; 93245900 2; 93585800 2; 93926525 2; 94143280 2; 94268076 2; 94610454 2; 94953660 2; 94966795 2; 95297695 2; 95548245 2; 95642560 2; 95988256 2; 96334784 2; 96560646 2; 96682145 2; 96717335 2; 97030340 2; 97379370 2; 97729236 2; 98079939 2; 98431480 2; 98491965 2; 98783860 2; 99137080 2; 99491141 2; 99795696 2; 99846044 2; 99884400 2; 100201790 2; 100290905 2; 100558380 2; 100915815 2; 101274096 2; 101340876 2; 101633224 2; 101993200 2; 102114376 2; 102354025 2; 102715700 2; 103078226 2; 103441604 2; 103805835 2; 103962600 2; 104170920 2; 104536860 2; 104903656 2; 105271309 2; 105639820 2; 105835800 2; 106009190 2; 106308566 2; 106379420 2; 106750511 2; 107122464 2; 107495280 2; 107734200 2; 107868960 2; 108243505 2; 108618916 2; 108995194 2; 109372340 2; 109453344 2; 109658025 2; 109750355 2; 110129240 2; 110508996 2; 110889624 2; 111271125 2; 111469176 2; 111607501 2; 111653500 2; 112036750 2; 112420876 2; 112805879 2; 113191760 2; 113578520 2; 113582855 2; 113966160 2; 114354681 2; 114744084 2; 115134370 2; 115525540 2; 115584315 2; 115775100 2; 115917595 2; 116310536
2; 116704364 2; 116828271 2; 117099080 2; 117494685 2; 117612110 2; 117891180 2; 118030185 2; 118288566 2; 118686844 2; 119086015 2; 119486080 2; 119666470 2; 119759850 2; 119877472 2; 119887040 2; 120288896 2; 120691649 2; 121095300 2; 121499850 2; 121747626 2; 121905300 2; 122311651 2; 122391522 2; 122718904 2; 123127060 2; 123536120 2; 123855810 2; 123946085 2; 124356956 2; 124403620 2; 124768734 2; 125181420 2; 125595015 2; 125991255 2; 126009520 2; 126424936 2; 126841264 2; 127258505 2; 127676660 2; 128095730 2; 128154195 2; 128164707 2; 128515716 2; 128936619 2; 129024480 2; 129358440 2; 129781180 2; 130204840 2; 130344865 2; 130629421 2; 131054924 2; 131115985 2; 131128140 2; 131481350 2; 131908700 2; 132336975 2; 132563501 2; 132766176 2; 133196304 2; 133627360 2; 133784560 2; 134059345 2; 134153712 2; 134492260 2; 134810340 2; 134926106 2; 135360884 2; 135796595 2; 136233240 2; 136670820 2; 137085620 2; 137109336 2; 137548789 2; 137989180 2; 138430510 2; 138872780 2; 139315991 2; 139389580 2; 139760144 2; 140205240 2; 140364532 2; 140651280 2; 141098265 2; 141120525 2; 141546196 2; 141722460 2; 141995074 2; 142444900 2; 142895675 2; 143218999 2; 143347400 2; 143800076 2; 144084501 2; 144253704 2; 144708285 2; 145008513 2; 145163820 2; 145422675 2; 145620310 2; 146077756 2; 146475945 2; 146536159 2; 146803272 2; 146995520 2; 147455840 2;
147917120 2; 148379361 2; 148842564 2; 148897035 2; 149306730 2; 149771860 2; 150237955 2; 150705016 2; 151173044 2; 151348015 2; 151642040 2; 152112005 2; 152582940 2; 153054846 2; 153476148 2; 153527724 2; 153829130 2; 154001575 2; 154143080 2; 154476400 2; 154952200 2; 155117520 1; 155428976 2; 155906729 2; 156238908 2; 156340626 2; 156385460 2; 156865170 2; 157345860 2; 157827531 2; 158310184 2; 158793820 2; 158882750 2; 159278440 2; 159764045 2; 160250636 2; 160389488 2; 160738214 2; 161226780 2; 161455750 2; 161716335 2; 162206880 2; 162698416 2; 163011640 2; 163190944 2; 163684465 2; 164059875 2; 164178980 2; 164674490 2; 165170996 2; 165668499 2; 166167000 2; 166666500 2; 166695375 2; 167167000 2; 167549733 2; 167668501 2; 168171004 2; 168674510 2; 169179020 2; 169362501 2; 169684535 2; 170191056 2; 170230452 2; 170698584 2; 171207120
2; 171716665 2; 172061505 2; 172227220 2; 172738786 2; 173251364 2; 173764955 2; 174279560 2; 174792640 2; 174795180 2; 174963438 2; 175311816 2; 175829469 2; 176348140 2; 176867830 2; 177100560 2; 177232627 2; 177388540 2; 177556160 2; 177910271 2; 178433024 2; 178956800 2; 179481600 2; 180007425 2; 180352320 2; 180534276 2; 181062154 2; 181591060 2; 182120995 2; 182637273 2; 182651960 2; 183181376 2; 183183956 2; 183579396 2; 183716984 2; 184251045 2; 184786140 2; 185250786 2; 185322270 2; 185859436 2; 186043585 2; 186397639 2; 186936880 2; 187477160 2; 188018480 2; 188560841 2; 188939205 2; 189104244 2; 189648690 2; 190194180 2; 190578024 2; 190740715 2; 191288296 2; 191836924 2; 191868495 2; 192386600 2; 192937325 2; 193489100 2; 193536720 2; 194041926 2; 194595804 2; 194831715 2; 195150735 2; 195706720 2; 196263760 2; 196821856 2; 197381009 2; 197829126 2; 197941220 2; 198502490 2; 198792594 2; 199064820 2; 199628211 2; 200192664 2; 200758180 2; 200860990 2; 201324760 2; 201359550 2; 201892405 2; 202461116 2; 202927725 2; 203030894 2; 203601740 2; 203927570 2; 204173655 2; 204746640 2; 205320696 2; 205895824 2; 206253075 2; 206472025 2; 207029130 2; 207049300 2; 207288004 2; 207627650 2; 208207076 2; 208787579 2; 209369160 2; 209951820 2; 210165935 2; 210535560 2; 211120381 2; 211706284 2; 211915132 2; 212293270 2; 212881340 2; 213338251 2;
213470495 2; 214060736 2; 214652064 2; 215244480 2; 215553195 2; 215837985 2; 216071394 2; 216432580 2; 216546345 2; 217028266 2; 217625044 2; 218222915 2; 218618940 2; 218821880 2; 219421940 2; 219790485 2; 220023096 2; 220625349 2; 221228700 2; 221833150 2; 222438700 2; 223045351 2; 223070940 2; 223653104 2; 224261960 2; 224871920 2; 225150024 2; 225482985 2; 225792840 2; 226095156 2; 226387980 2; 226708434 2; 227322820 2; 227938315 2; 228554920 2; 229172636 2; 229741876 2; 229791464 2; 230411405 2; 231032460 2; 231654630 2; 231917400 2; 232277916 2; 232902319 2; 233132900 2; 233527840 2; 234154480 2; 234531275 2; 234782240 2; 235411121 2; 236041124 2; 236561325 2; 236672250 2; 237093780 2; 237304500 2; 237937875 2; 238572376 2; 239208004 2; 239844760 2; 240027425 2; 240482645 2; 241121660 2; 241761806 2; 242403084 2; 243045495 2; 243531475
2; 243689040 2; 244222650 2; 244333720 2; 244979536 2; 245626489 2; 246274580 2; 246923810 2; 247073751 2; 247574180 2; 248225691 2; 248878344 2; 249532140 2Zelf proberen