Inhoud
Inleiding
Een tijdje geleden gaf een bevriende wiskundige mij de volgende puzzel: Voor welke n kun je een driehoek, gestapeld met zeshoekjes, met basis n geheel vullen met triplets, waarbij een triplet een driehoekje met 3 zeshoekjes is?
In dit artikel wil ik u meenemen met mijn zoektocht naar de oplossing van deze puzzel.
De puzzel
Eerst maar even wat meer duiding over de puzzel.
Een triplet is dus een driehoekje gebouwd uit 3 zeshoekjes:

Omdat de punt van deze triplet naar boven wijst noem ik deze “up”.
Dan bestaat er natuurlijk ook een “down”:

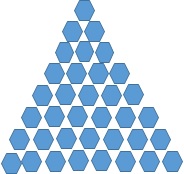
En zo ziet dan een driehoek gebouwd uit zeshoekje met basis n eruit:

Omdat de basis van deze driehoek uit 5 zeshoekjes bestaat noem ik deze t5.
En de vraag is dus nu voor welke n tn geheel te vullen is met up’s en down’s.
Ik neem u mee…
Naar de oplossing
Een eerste analyse van dit probleem is dat tn in ieder geval een 3-voud moet zijn omdat een triplet (up of down) uit 3 zeshoekjes bestaat.
Om te bepalen hoeveel zeshoekjes er in tn zitten moeten we de volgende som oplossen: 1 + 2 + 3 + 4 + … + n-1 + n.
En als je deze som onder elkaar zet dan kun je er een handigheidje in ontdekken:
1-----------------------------------------------------
2------------------------------------- |
3--------------------- | |
4------ | | |
… | ->(n-3+4=n+1)| ->(n-2+3=n+1) | ->(n-1+2=n+1) | ->(n+1)
n-3----- | | |
n-2-------------------- | |
n-1------------------------------------ |
n-----------------------------------------------------
----- +
Je komt dus steeds paren van (n+1) tegen. Een paar bestaan uit 2, dus voor een som die doorloopt tot n heb je ½n paren. De som van 1 t/m n is dan dus niets anders dan ½n(n+1).
Dit wetende is nu de vraag voor welke n ½n(n+1) een 3-voud is.
Maar even wat getallen voor n uitproberen:
| n |
1/2n(n+1) |
3-voud |
| 0 |
0 |
3-voud |
| 1 |
1 |
|
| 2 |
3 |
3-voud |
| 3 |
6 |
3-voud |
| 4 |
10 |
|
| 5 |
15 |
3-voud |
| 6 |
21 |
3-voud |
| 7 |
28 |
|
| 8 |
36 |
3-voud |
| 9 |
45 |
3-voud |
| 10 |
55 |
|
| 11 |
66 |
3-voud |
Uit bovenstaande tabel lijkt het erop dat als n of n+2 een 3-voud is dat ½n(n+1) ook een 3-voud is.
En omdat dit artikel met wiskunde te maken heeft moeten we dat dan ook maar even bewijzen.
De stelling is dus: Als n een 3-voud is of als n+2 een 3-voud is dan is ½n(n+1) ook een 3-voud.
We beginnen het bewijs met een lemma, dat is een hulpstelling die zo voor de hand ligt dat we er geen bewijs bij leveren.
Lemma: Als je een 3-voud met een ander natuurlijk getal vermenigvuldigt is het product ook weer een 3-voud.
Bewijs:
I: n=3v à ½(3v)(3v+1) à ½(9v2+3v) (x2 [lemma]) à 9v2+3v = 3(3v2+1), is dus een 3-voud.
II: n=3v+1 à ½(3v+1)(3v+2) à ½(9v2+9v+2) (x2 [lemma]) à 9v2+9v+2 = 3(3v2+3v)+2, is dus geen 3-voud.
III: n=3v+2 à ½(3v+2)(3v+3) à ½(9v2+15v+6) (x2 [lemma]) à 9v2+15v+6 = 3(3v2+5v+2), is dus een 3-voud.
Q.E.D.
Nu we dit weten kunnen we wat gerichter gaan zoeken naar driehoeken die zouden kunnen voldoen om geheel te vullen met triplets.
We hoeven dus niet te kijken naar bijvoorbeeld t4, omdat t4 geen 3-voud aan zeshoekjes heeft:

Laten we dus maar eens beginnen met t5:

Als je even puzzelt dan zie je dat de hoekpunten altijd gevuld moeten worden met een up:

Voor de blauwe zeshoekjes blijven er nu de volgende mogelijkheden over:
Hieruit blijkt dat er voor t5 geen oplossing is; t5 voldoet dus niet.
En na (heel) veel puzzelen blijkt dat ook t6 en t8 geen oplossing hebben:
Hier ontstond het vermoeden dat het wel eens lastig zou kunnen worden om een oplossing te vinden, maar na lang puzzelen… t9:
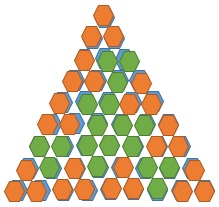
De eerste die een oplossing heeft!
En tot mijn verbazing en verwondering bleek t11 ook te kunnen:
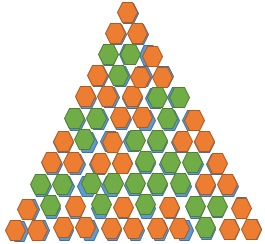
Resultaat!
En toen begon het “grote denken”.
Waarom de één wel en de andere niet? Wat is er aan de hand met de tn’s die niet lukken ten opzichte van de tn’s die wel lukken?
Op een strandwandeling van Den Haag naar Hoek van Holland overdacht ik het een en ander. En daar was opeens de ingeving. Hoe weet ik niet, maar het bleek mijn “Eureka” naar de oplossing te zijn.
Bij de driehoeken die niet kunnen blijven er altijd 3 over die dan wel horizontaal, verticaal of diagonaal zijn te maken, maar niet in een driehoek-vorm. Ik ben deze triples (let op, dus geen triplets) H3 gaan noemen en bedacht me dat ik het aantal H3’s per driehoek moest gaan bepalen.
Wederom thuis gekomen ben ik aan de slag gegaan.
Uitgezet in een tabel kwam ik tot de volgende resultaten:
| n |
1/2n(n+1) |
3-voud |
aantal triplets |
resultaat |
ups |
downs |
H3 |
| 0 |
0 |
3-voud |
0 |
|
|
|
|
| 1 |
1 |
|
|
|
|
|
|
| 2 |
3 |
3-voud |
1 |
voldoet, triviaal |
1 |
0 |
0 |
| 3 |
6 |
3-voud |
2 |
voldoet niet |
|
|
1 |
| 4 |
10 |
|
|
|
|
|
2 |
| 5 |
15 |
3-voud |
5 |
voldoet niet |
|
|
3 |
| 6 |
21 |
3-voud |
7 |
voldoet niet |
|
|
5 |
| 7 |
28 |
|
|
|
|
|
7 |
| 8 |
36 |
3-voud |
12 |
voldoet niet |
|
|
9 |
| 9 |
45 |
3-voud |
15 |
voldoet |
9 |
6 |
12 |
| 10 |
55 |
|
|
|
|
|
15 |
| 11 |
66 |
3-voud |
22 |
voldoet |
13 |
9 |
18 |
Bij de driehoeken die voldoen (t2, t9 en t11) is H3 even, ofwel een 2-voud. Bij de driehoeken die niet voldoen (t3, t5, t6 en t8) is H3 oneven, dus geen 2-voud.
Zou dit vermoeden juist kunnen zijn?
Het aantal H3’s van t12 is 22, dus zou t12 moeten kunnen. En zie het resultaat na wat puzzelen:
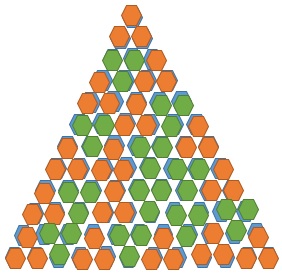
Het aantal H3’s van t14 is 30, dus ook even. En dus moet t14 ook geheel te vullen zijn:
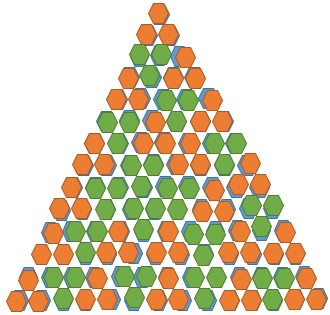
Het aantal H3’s van t15 is 35 en na heel veel gepuzzel kwam ik niet tot een oplossing.
Met aan zekerheid grenzende waarschijnlijkheid concludeer ik dat mijn stelling van de H3’s juist is.
De vraag is nu echter of er een formule is die de H3’s bij een bepaalde tn kan berekenen en voor welke n deze formule dan een 2-voud is.
Hier komt wat saai werk voor aan te pas en ik zal u deze details besparen.
De formule voor het aantal H3’s bij gegeven n is: [1/6n(n-1)]. De blokhaken hebben hier de wiskundige betekenis van de “entier”-functie. Dit betekent dat het resultaat van 1/6n(n-1) naar beneden moet worden afgerond op nul decimalen, dus naar het eerste natuurlijke getal kleiner of gelijk aan het resultaat van de formule.
En de laatste vraag die nu nog moet worden beantwoord is voor welke n de formule [1/6n(n-1)] een 2-voud oplevert.
Daarvoor breiden we de laatste tabel nog even iets verder uit:
| n |
1/2n(n+1) |
3-voud |
aantal triplets |
resultaat |
ups |
downs |
H3 |
[1/6n(n-1)] |
| 0 |
0 |
3-voud |
0 |
|
|
|
|
|
| 1 |
1 |
|
|
|
|
|
|
|
| 2 |
3 |
3-voud |
1 |
voldoet, triviaal |
1 |
0 |
0 |
0 |
| 3 |
6 |
3-voud |
2 |
voldoet niet |
|
|
1 |
1 |
| 4 |
10 |
|
|
|
|
|
2 |
2 |
| 5 |
15 |
3-voud |
5 |
voldoet niet |
|
|
3 |
3 |
| 6 |
21 |
3-voud |
7 |
voldoet niet |
|
|
5 |
5 |
| 7 |
28 |
|
|
|
|
|
7 |
7 |
| 8 |
36 |
3-voud |
12 |
voldoet niet |
|
|
9 |
9 |
| 9 |
45 |
3-voud |
15 |
voldoet |
9 |
6 |
12 |
12 |
| 10 |
55 |
|
|
|
|
|
15 |
15 |
| 11 |
66 |
3-voud |
22 |
voldoet |
13 |
9 |
18 |
18 |
| 12 |
78 |
3-voud |
26 |
voldoet |
15 |
11 |
22 |
22 |
| 13 |
91 |
|
|
|
|
|
26 |
26 |
| 14 |
105 |
3-voud |
35 |
voldoet |
20 |
15 |
30 |
30 |
| 15 |
120 |
3-voud |
40 |
voldoet w niet |
|
|
35 |
35 |
| 16 |
136 |
|
|
|
|
|
40 |
40 |
| 17 |
153 |
3-voud |
51 |
voldoet w niet |
|
|
45 |
45 |
| 18 |
171 |
3-voud |
57 |
voldoet w niet |
|
|
51 |
51 |
| 19 |
190 |
|
|
|
|
|
57 |
57 |
| 20 |
210 |
3-voud |
70 |
voldoet w niet |
|
|
63 |
63 |
| 21 |
231 |
3-voud |
77 |
voldoet w wel |
|
|
70 |
70 |
| 22 |
253 |
|
|
|
|
|
77 |
77 |
| 23 |
276 |
3-voud |
92 |
voldoet |
|
|
84 |
84 |
Uit deze tabel kun je nu destilleren dat wanneer n+3, n+1, n of n+2 een 12-voud is [1/6n(n-1)] een 2-voud is.
Het bewijs gaat analoog aan het eerste bewijs van dit artikel, maar is saai en tijdrovend en laat ik daarom achterwege.
De puzzel is wat mij betreft opgelost en ik hoop dat ik een kijkje heb kunnen geven in het proces naar de oplossing toe.
Wiskunde is en blijft toch een mooi en boeiend vakgebied!
[Oplossing raadsel 8]
![]()
![]()